Sortieren mit dem Computer (5)

Ein ausführlicher Geschwindigkeitsvergleich aller bisher erarbeiteten Sortieralgorithmen soll die Spreu vom Weizen trennen. Und ein weiteres Sortieralgorithmus wird vorgestellt.

Entgegen der anderslautenden Vorhersage im letzten Teil unseres Kurses, soll heute noch einmal auf Sortieralgorithmen in Basic eingegangen werden. Dieser Entschluß wurde aus mehreren Gründen gefaßt.

Erstens trafen nach Erscheinen der letzten Ausgabe mehrere interessante Beiträge zum Thema Sortieren in der Redaktion ein. Zweitens soll noch einmal ein grafischer Vergleich sämtlicher Routinen stattfinden, und drittens werden wir uns heute noch ein wenig mit den Vor-und Nachteilen der einzelnen Sortiermethoden beschäftigen.

Als erstes soll eine Verbesserung an den Mann gebracht werden. Heinrich Studer schickte der Redaktion einen Sortieralgorithmus, der dem schon bekannten Straight Selection stark ähnelt, wegen seines einfacheren Aufbaus jedoch weniger Speicherplatz benötigt. Der Einfachheit halber soll dieser Sortieralgorithmus den Namen Minisort bekommen.

Wie Sie aus dem Flußdiagramm in Bild 1 sehen können, besteht Minisort aus zwei geschachtelten FOR-NEXT-Schleifen. In der äußeren Schleife wird jeweils der Reihe nach ein Element genommen und mit sämtlichen Elementen der inneren Schleife verglichen. Wird während eines Vergleichs festgestellt, daß das andere Element aus dem Restfeld kleiner als unser Vergleichswert ist, so werden beide Variablen vertauscht.

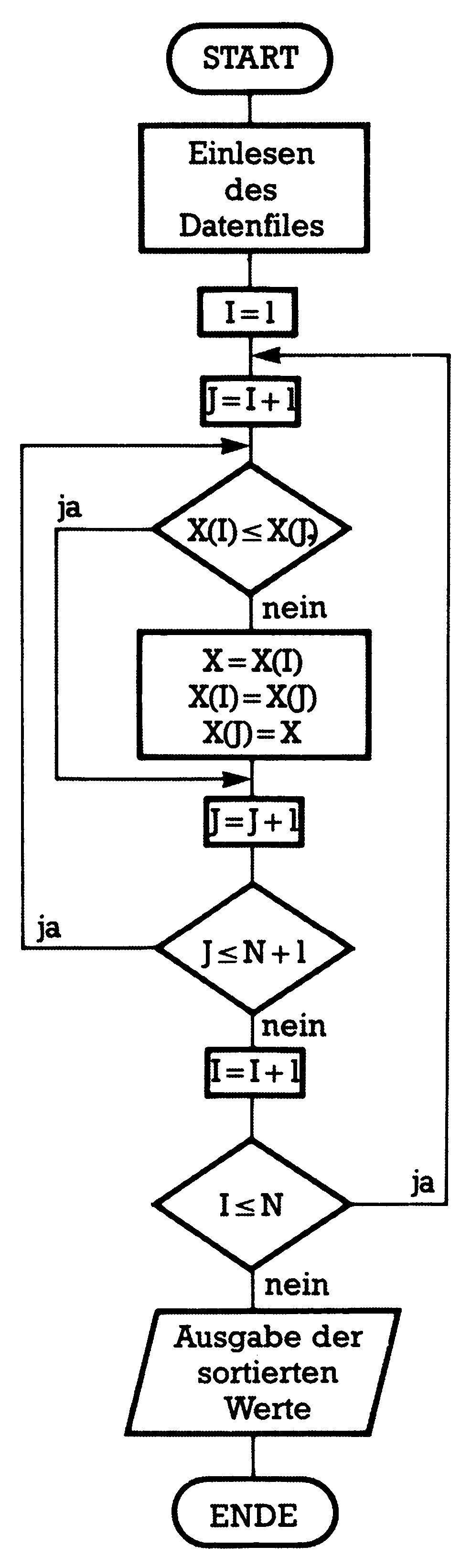
Ist die innere Schleife also einmal durchlaufen worden, so befindet sich das kleinste Element des Gesamtfeldes nun an erster Stelle.

Jetzt wird in der äußeren Schleife zum nächsten Element übergegangen, wobei dieses wiederum mit dem Restfeld verglichen wird… und so weiter, bis man beim letzten Element angekommen ist. Es muß sich hierbei dann zwangsläufig um den größten Wert handeln.

Für Minisort (Listing 1) wie auch für unsere übrigen Sortieralgorithmen gilt, daß sie das Hauptprogramm für ihren Betrieb benötigen. Das Hauptprogramm dient der Erstellung der verschiedenen Arrays und der Anzeige der erstellten und sortierten Felder. In Listing 2 wurde auch diesmal wieder das Hauptprogramm abgedruckt, da es um ein paar Sachen erweitert wurde. Es ist jetzt mit der Option »von Hand erstellen« zusätzlich möglich, jeweils vorwärts und rückwärts sortierte Felder zu erstellen, um die »Testkandidaten« (sprich: Sortierprogramme) auf Herz und Nieren zu testen.

10040 ti$="000000"
10050 for x=1 to a-1
10060 for y=x+1 to a
10070 if a$(x)<=a$(y)then 10090
10080 s$=a$(x):a$(x)=a$(y):a$(y)=s$
10090 next y,x

10 rem erstellen eines feldes zum
20 rem sortieren.
30 rem das erstellen kann zufaellig
40 rem oder geziehlt (durch eingabe)
50 rem erfolgen.
60 rem
70 rem sortieralgorithmen erhalten die
80 rem zeilennummern von 1000 bis 10000
90 rem sie benoetigen jeweils diesen
99 rem vorspann zur ausfuehrung.
100 rem herstellung eines arrays:
110 rem arrayvariable      - a$
120 rem schleifenvariablen - x, y, z
130 rem hilfsvariablen     - b$, c$, d$
140 rem dreiecktausch mit  - s$
150 print"{clr}":clr
160 print"soll von {rvon}h{rvof}and oder {rvon}z{rvof}ufaellig erstellt":print
170 input"werden ";x$
180 ifx$<>"h"andx$<>"z"then150
190 ifx$="h"thengosub220:gosub1000:goto210
200 gosub220:gosub2000
210 goto4000: rem weitermachen
220 rem anzahl der elemente bestimmen
230 print:input"anzahl der elemente ";a
240 if a>10000thenprint:print"zu viele elemente":goto230
250 ifa<10thenprint:print"zu wenige elemente":goto230
255 dim a$(a)
260 input"{down}{down}{rvon}d{rvof}rucker oder {rvon}b{rvof}ildschirm ";y$
270 ify$<>"d"andy$<>"b"then260
280 ify$="d"thend=4:goto300
290 d=3
300 return
1000 rem eingabe von hand
1010 print"{clr}v oder r";
1020 inputx$:ifx$<>"r"andx$<>"v"then1020
1030 r=1:x1=1:x2=a
1040 ifx$="r"thenr=-1:x1=a:x2=1
1050 z1=65:z2=65:z3=65:forx=x1tox2stepr
1060 a$(x)="":a$(x)=chr$(z1):z1=z1+1:ifz1>90thenz1=65
1062 a$(x)=chr$(z2)+a$(x):ifz1=90thenz2=z2+1:ifz2>90thenz2=65
1064 a$(x)=chr$(z3)+a$(x):ifz2=90thenz3=z3+1:ifz3>90thenz3=65
1070 nextx
1080 return
2000 rem zufaellige eingabe
2010 print"{clr}"
2020 print:print"es werden jetzt"a" elemente zufaellig":print:print"ausgewaehlt"
2030 print:print"jedes element besteht aus 3 zeichen.":print:print
2040 forx=1toa
2050 a$(x)=""
2060 fory=1to3:a$(x)=a$(x)+chr$(int(rnd(ti)*25)+65):nexty
2070 nextx
2080 return
3000 rem zwischenausgabe der elemente
3010 for i=1toa-9step10
3020 for j=itoi+9:print#1,a$(j)" ";:nextj
3030 print#1:nexti: print#1
3040 return
4000 rem weitermachen
4005 open1,d
4010 print"{clr}ausgabe des erstellten feldes"
4020 print
4030 gosub3000
4040 rem sortierung startet
4050 rem

50000 t$=ti$:rem endebehandlung
50010 print#1
50020 gosub 3000
50030 print#1,a;" elemente"
50040 print#1:print#1:print#1,t$:close1
50050 end

Um Ihnen jedoch einen großen Teil der Arbeit abzunehmen, habe ich für diese Folge unseres Kurses noch einmal sämtliche Sortierprogramme, die bisher besprochen wurden, in den drei Bereichen »Feld unsortiert«, »Feld vorwärts sortiert« und »Feld rückwärts sortiert« untersucht. Wir werden nachher noch ausführlich auf die Ergebnisse dieses »Monstertests« eingehen.

Jetzt jedoch noch zu einem anderen Sortierprogramm, das uns Horst Armin Kosog eingesandt hat. Es trägt den Namen »Mischsort« und wurde von besagtem Absender anhand einer Aufgabenstellung aus einem Informatikbuch (H. Balzert, Informatik 1, Hueber-Holzmann Verlag, München 1976, Seite 210) erstellt und selbständig weiterentwickelt.

Das Prinzip dieses Sortieralgorithmus ist folgendes:

Ähnlich wie bei Quicksort wird das zu sortierende Array bei Mischsort in Untereinheiten (Teilfelder) untergliedert. Diese Teilfelder fangen bei der Größe 2 an und nehmen dann im Quadrat an Umfang zu (4,8,16,…).

Zuerst werden die Untereinheiten der Größe 2 jeweils für sich sortiert, so daß wir A/2 (A ist die Anzahl der Elemente im Gesamtfeld), sortierte Teilfelder erhalten.

Jeweils zwei benachbarte Teilfelder werden nun »zusammengemischt« und wiederum sortiert.

Setzt man dies durch das gesamte Array fort, so erhalten wir nun A/4 sortierte Teilfelder der Länge 4.

Als nächstes werden jeweils zwei benachbarte Teilfelder der Länge 4 zusammengemischt und sortiert… und so weiter, bis schließlich nur noch ein (Teil) Feld übrigbleibt, nämlich das Gesamtfeld.

Diese Arbeitsweise sei noch einmal in Bild 2 grafisch dargestellt.

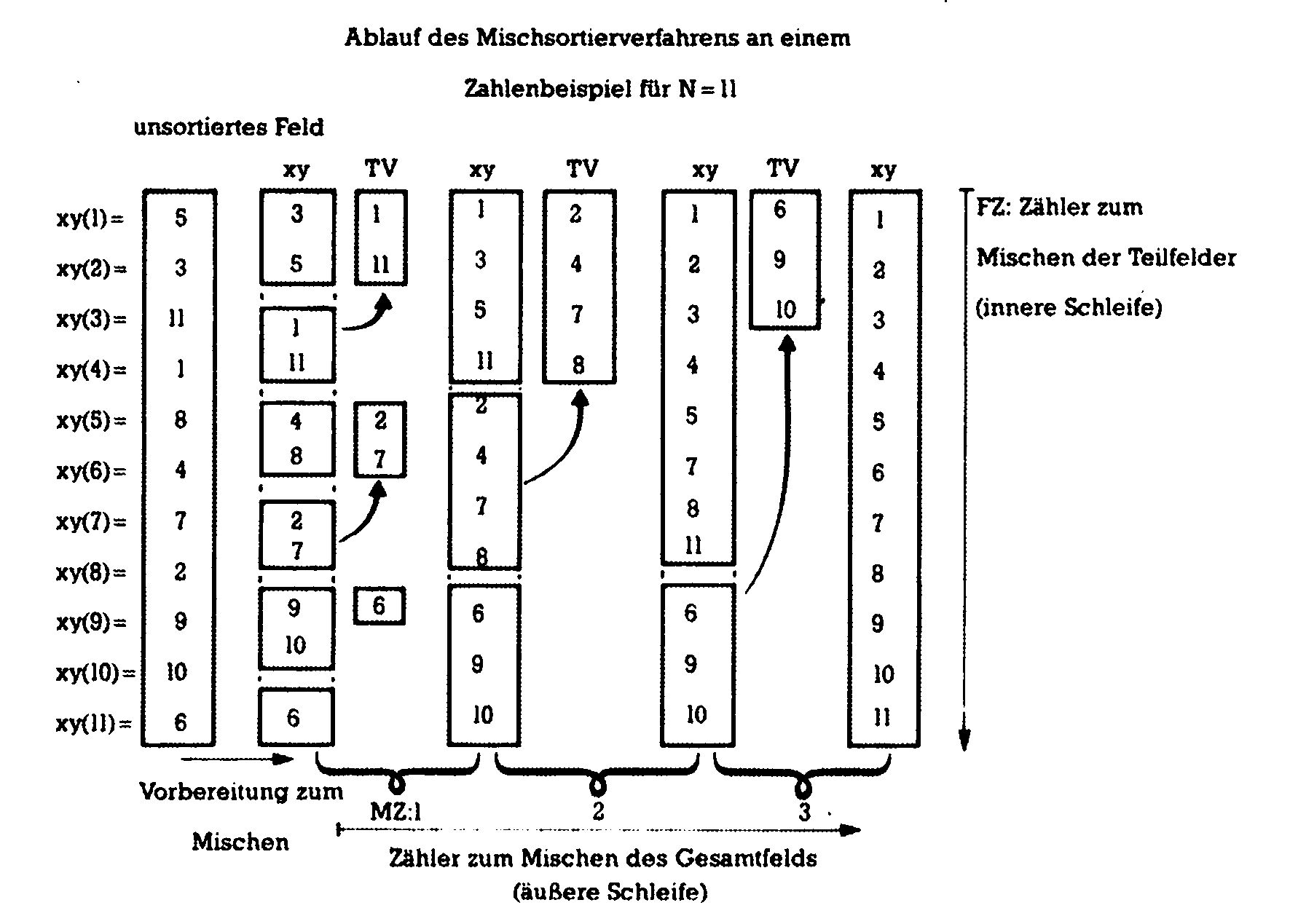
Damit Sie beim Abtippen von Listings nicht aus der Übung kommen, haben wir auch zu Mischsort ein Programm (Listing 3). Es muß, wie alle übrigen Algorithmen auch, in unser Hauptprogramm eingefügt werden.

10040 ti$="000000"
10050 zf=int(a/2+.5):dimtv$(zf)
10060 forx=2toastep2
10070 ifa$(x-1)>a$(x)thentv$(0)=a$(x-1):a$(x-1)=a$(x):a$(x)=tv$(0)
10080 nextx:ifa<3then 50000
10090 lf=1:formz=1toint(log(a-1)/log(2))
10100 zf=int(zf/2+.5):lf=2*lf
10110 forfz=1tozf:a1=1+2*lf*(fz-1):a2=a1+lf:e1=a2-1:e2=e1+lf
10120 ife2<=athenet=lf:goto10150
10130 ifa<a2then10230
10140 e2=a:et=a+1-a2
10150 forx=1toet:tv$(x)=a$(x+e1):next
10160 forx=e2toa1step-1
10170 ifa$(e1)<tv$(et)then10200
10180 a$(x)=a$(e1):e1=e1-1:ife1>=a1then10220
10190 fory=x-1toa1step-1:a$(y)=tv$(et):et=et-1:nexty:goto10210
10200 a$(x)=tv$(et):et=et-1:ifet>=1then10220
10210 x=a1
10220 nextx
10230 nextfz,mz

Ein dokumentiertes Flußdiagramm zu Mischsort ist in Bild 3 abgedruckt.

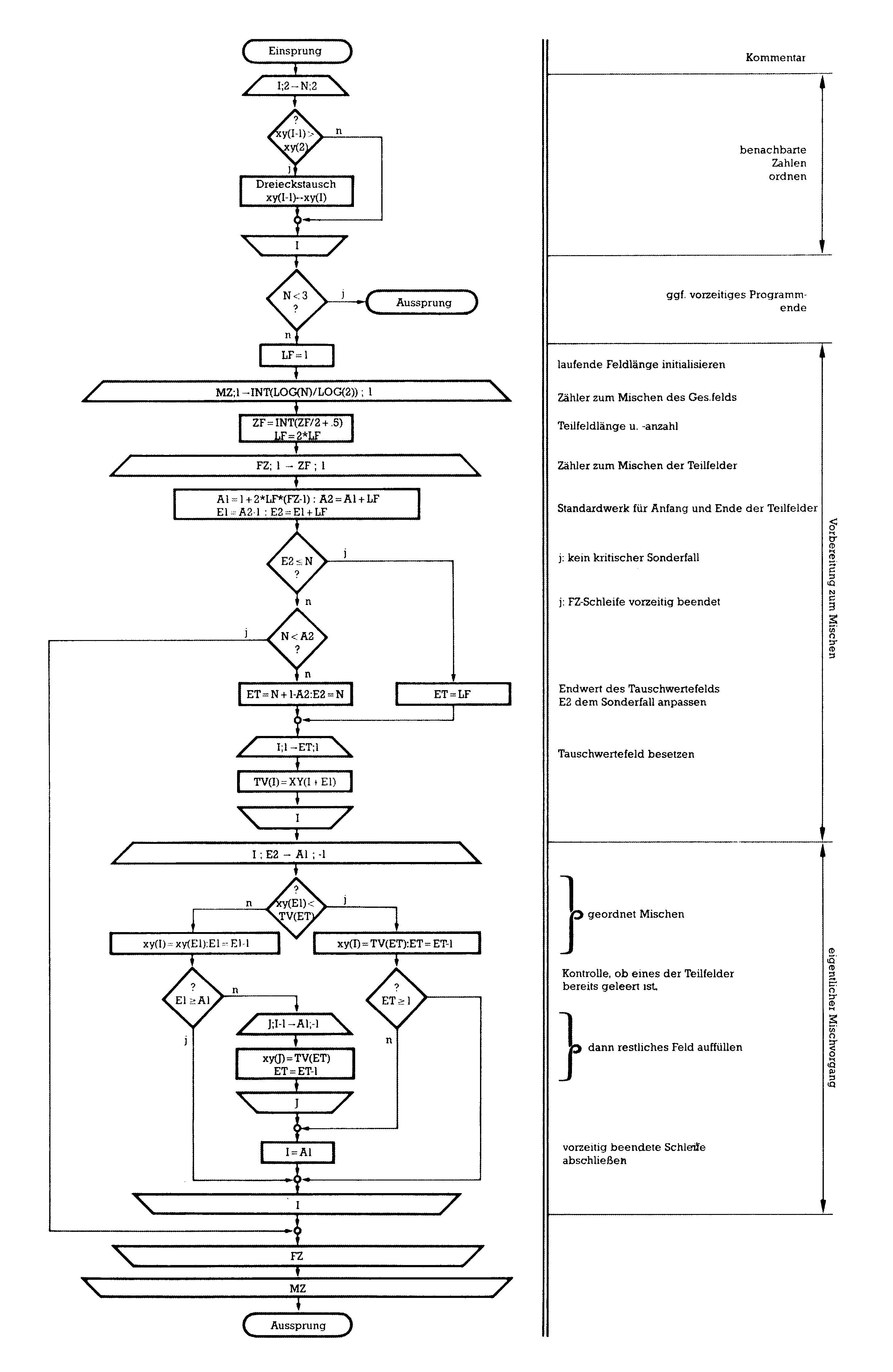
Schneller als Quicksort!

Mit dieser Überschrift stellte kürzlich eine Zeitschrift für Personal Computer (Computer persönlich, Ausgabe 14/85) ein neues Sortierverfahren vor. Das Programm lief ursprünglich auf einem CBM 8032 und machte also keine Mühe bei der Umstellung auf den Commodore 64. Ein derartiger Beitrag darf natürlich in unserem Kurs nicht unerwähnt und unbesprochen bleiben, weshalb ich das Programm in unsere Reihe der Sortiermethoden aufgenommen habe.

Das interessante an Supersort (so heißt das Wunderprogramm) ist sicherlich die Art und Weise, wie bei diesem Programm Zeit gespart wird. Wir haben es hier nämlich eigentlich mit zwei Sortierprogrammen zu tun.

Das eine Sortierprogramm davon kennen wir bereits. Es handelt sich um Bubblesort 2, also die verbesserte Version des ursprünglichen Bubblesort. (Wir erinnern uns: die Verbesserung von Bubblesort bestand im Einführen eines Zeigers, der dafür sorgte, daß Bubblesort mit der Arbeit aufhört, sobald keine Vertauschungen mehr stattfinden. Dieser »Kunstgriff« sorgte dafür, daß Bubblesort 2 bei Feldern, die insgesamt schon sortiert sind, einige wenige Elemente aber neu eingeordnet werden müssen, äußerst schnell wird und die kürzesten Sortierzeiten überhaupt erreichen kann.).

Bei Supersort nutzt man nun die Tatsache, daß Bubblesort bei Feldern bis maximal zehn Elementen sehr schnell arbeitet. Es wird also das Gesamtfeld einfach in Teilfelder mit maximal zehn Elementen aufgeteilt, die dann alle einzeln von Bubblesort nachsortiert werden.

Damit die Teilfelder dann auch in der richtigen Reihenfolge stehen, wird das Gesamtfeld vorsortiert, wobei die Teilfelder entsprechend der Anfangsbuchstaben der Feldelemente zusammengestellt werden.

Das Flußdiagramm von Supersort sehen Sie in Bild 4, wobei auf die detaillierte Darstellung von Bubblesort verzichtet wurde.

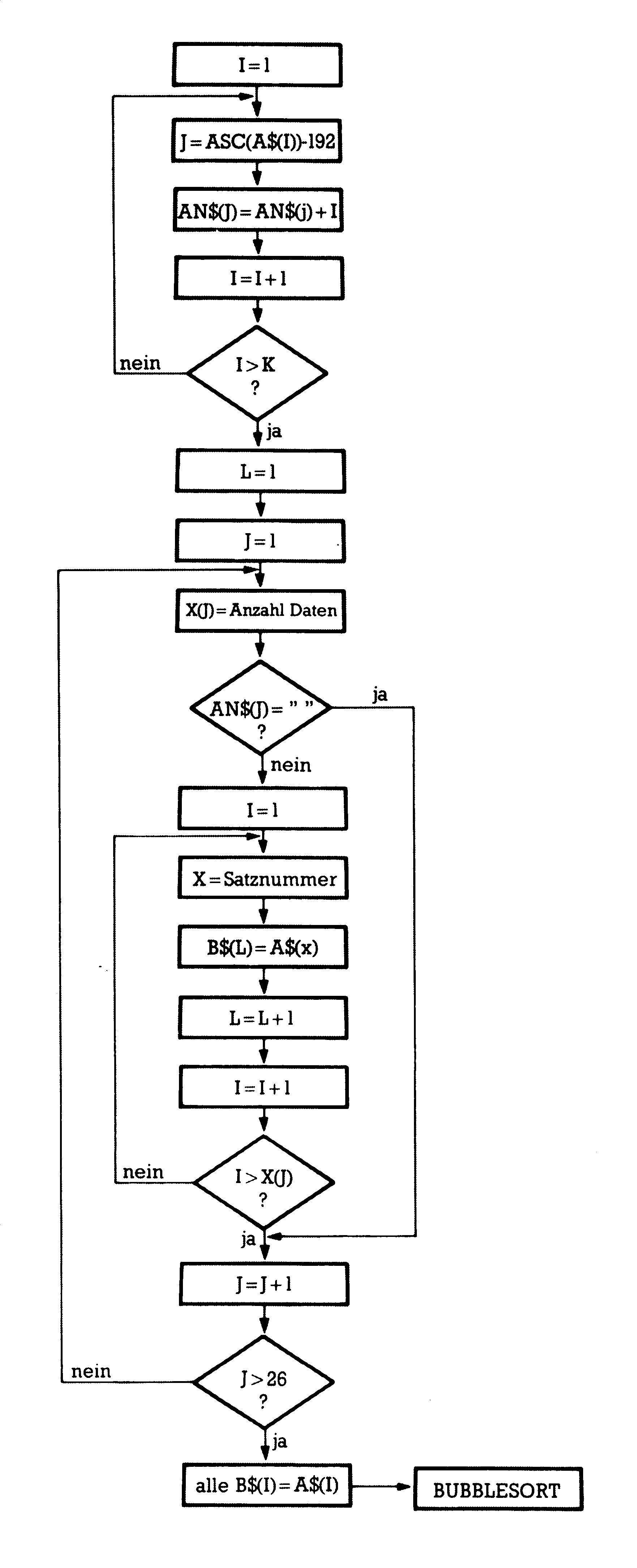
Auf unser Hauptprogramm zugeschnitten können Sie Supersort in Listing 4 finden. Es kann ohne weitere Änderungen mit den anderen Routinen dieses Kurses zusammenarbeiten.

10000 ti$="000000":dimzp$(a),an$(26),x(26),b$(a)
10040 forii=1to26
10050 an$(ii)="":x(ii)=0
10060 nextii
10070 ifasc(a$(1))>64thenmin=64
10080 ifasc(a$(1))>192thenmin=192
10085 for ii=1toa
10090 jj=asc(a$(ii))-min
10100 ifjj<0thenjj=26
10110 an$(jj)=an$(jj)+str$(ii+100)
10120 nextii
10130 l=1
10140 forjj=1to26
10150 x(jj)=len(an$(jj))/4
10160 ifan$(jj)=""then10210
10170 forii=1tolen(an$(jj))step4
10180 x=(val(mid$(an$(jj),ii,4))-100)
10190 b$(l)=a$(x):a$(x)="":l=l+1
10200 nextii
10210 nextjj
10220 forii=1toa
10230 a$(ii)=b$(ii):b$(ii)=""
10240 nextii
10250 y=0
10260 forl=1to26
10270 x=y+1:y=x+x(l)-1
10280 ifx(l)=0orx(l)=1then10340
10290 forjj=y-1toxstep-1:fl=-1
10300 forn=xtojj
10310 ifa$(n)>a$(n+1)thenfl=0:te$=a$(n):a$(n)=a$(n+1):a$(n+1)=te$
10320 nextn
10330 ifnotflthennextjj
10340 nextl

Nachdem wir nun eine ziemliche Menge von verschiedenen Sortieralgorithmen kennen, sollen diese jetzt auch einmal im Vergleich betrachtet werden. Für den Anwender stellt sich in der Regel nur die Frage, welches Sortierprogramm er für seine Problemlösung am besten verwenden kann, und diese Frage ist mitunter nicht so leicht zu beantworten.

Für den Vergleichstest habe ich folgende Sortierprogramme verwendet:

Straight Insertion, Straight Selection, Bubblesort 2, Shellsort, Heapsort, Quicksort, Supersort und Mischsort.

Fangen wir mit den Bedingungen des Tests an. Die einzelnen Programme wurden mit vorsortierten und unsortierten Feldern getestet, wobei nur Stringarrays verwendet wurden. Während des Tests wurde die Anzahl der Elemente jedesmal vergrößert, damit sich anschließend ein Kurvendiagramm darstellen ließ.

Die ersten fünf Algorithmen wurden mit 10, 20, 50, 100 und 200 Elementen gemessen (Bubblesort nur bis 100). Die drei schnelleren Methoden Quicksort, Supersort und Mischsort wurden auch noch mit 500 Elementen geprüft.

Höhere Anzahlen von Feldelementen waren aus mehreren Gründen nicht nötig.

Erstens steigt die Sortierzeit einiger Routinen nach kurzer Zeit enorm an, was zu Werten außerhalb der Grafikskala führt.

Zweitens kommt es zu Konflikten mit der Geduld des Testers, wenn zu viele Elemente verwendet werden (Bubblesort 2 benötigte beispielsweise bei 1000 rückwärts geordneten Elementen sage und schreibe 6702 Sekunden; das sind 1 Stunde 51 Minuten und 42 Sekunden!). Und drittens kommt ab einer gewissen Zahl an Feldelementen noch ein ganz anderes Problem zum Tragen, das sich Garbage Collection nennt und auch den schnellsten Sortieralgorithmus zur Verzweiflung bringt.

Nun also zur Besprechung der Testergebnisse:

Sehen Sie sich einmal Bild 5 an, es enthält die Testergebnisse von Bubblesort einmal grafisch dargestellt.

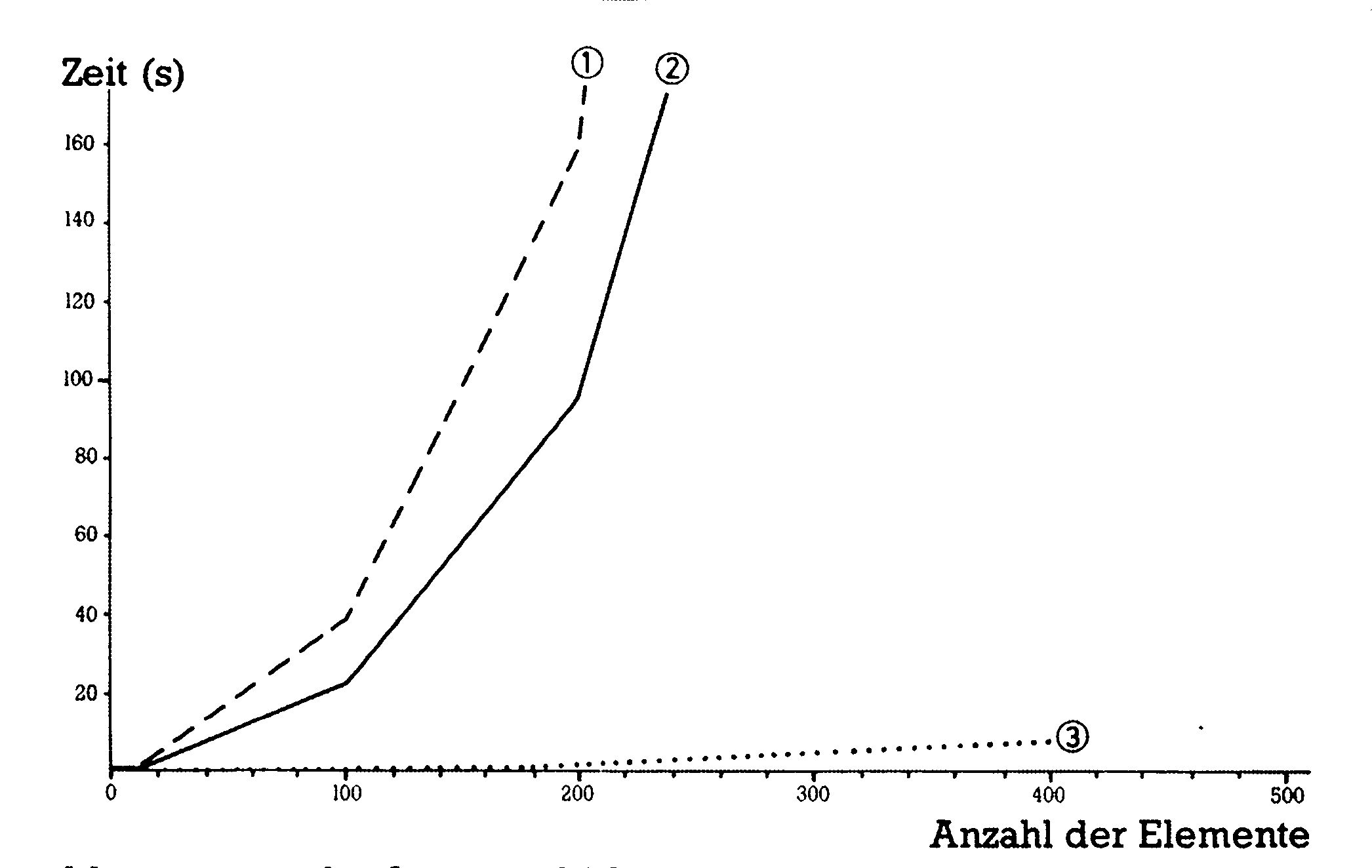
Auf der X-Achse ist dabei die Anzahl der Elemente und auf der Y-Achse die benötigte Sortierzeit in Sekunden angeführt.

Wie man erkennen kann, steigt die Sortierzeit dabei exponentiell an, was auf lange Wartezeiten hoffen läßt. Eine Ausnahme bilden jedoch die schon sortierten Felder. Hier zeigt sich Bubblesort von seiner besten Seite. Es stellt innerhalb von wenigen Sekunden fest, ob ein Feld schon sortiert ist und eignet sich deshalb hervorragend zum Einordnen weniger Elemente in ein großes sortiertes Feld.

Bild 6 zeigt Straight Insertion in Aktion. Dieses Sortierprogramm zeigt ein ähnliches Verhalten wie Bubblesort und ist sogar noch ein wenig schneller. Die Anwendungsgebiete liegen also auf der gleichen Ebene wie bei Bubblesort: Einordnen weniger Elemente in ein großes vorsortiertes Feld (vielleicht ließe sich durch Straight Insertion Supersort noch ein wenig mehr »aufmöbeln« ?!?).

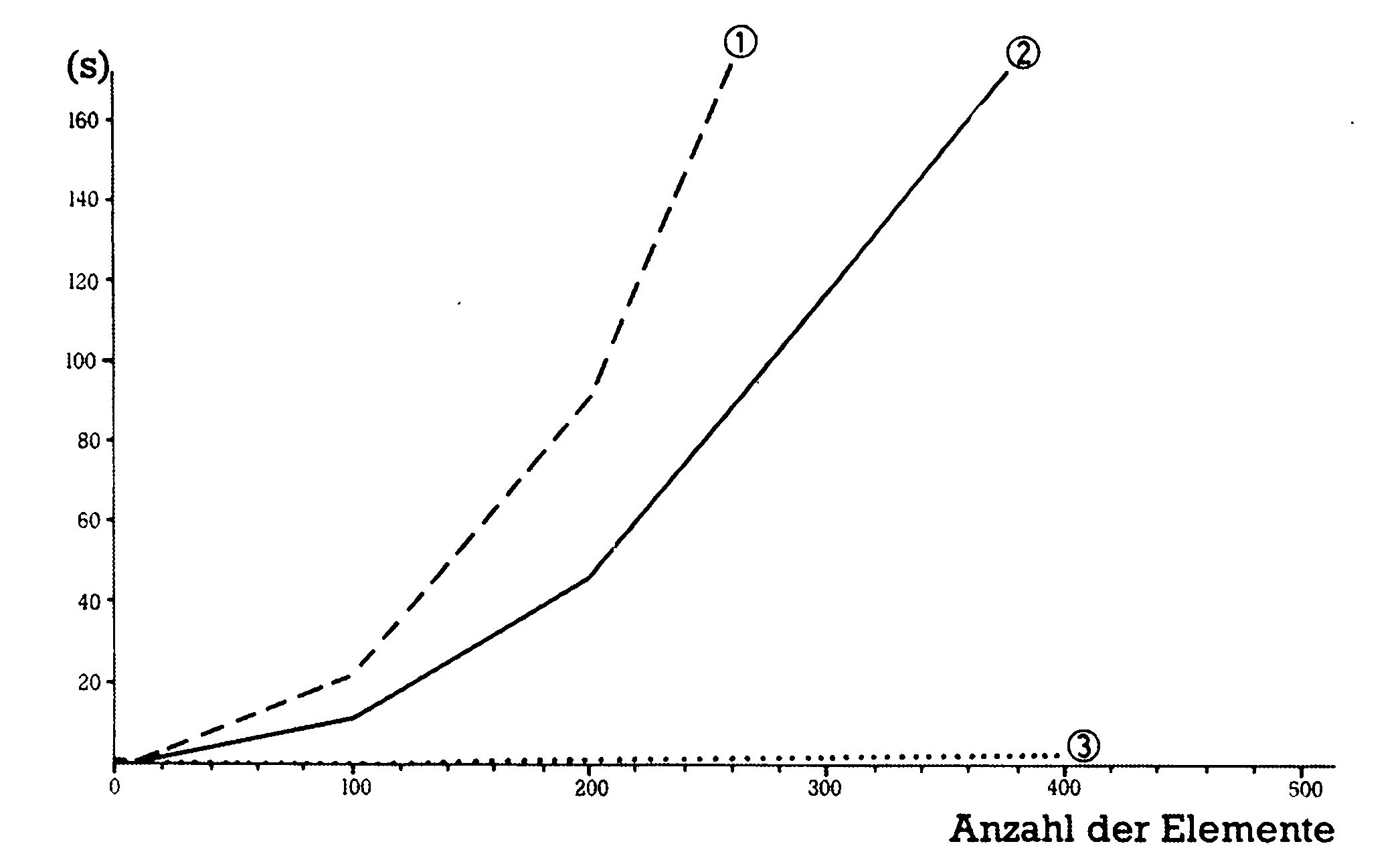
Bild 7 macht uns mit der Charakteristik von Straight Selection vertraut, und man kann nicht verhehlen, daß dieser Sortieralgorithmus auf allen Gebieten langsam und uneffektiv arbeitet. Er lohnt sich der Einfachheit halber bei sehr kleinen Feldern mit unterschiedlichen Sortierungen.

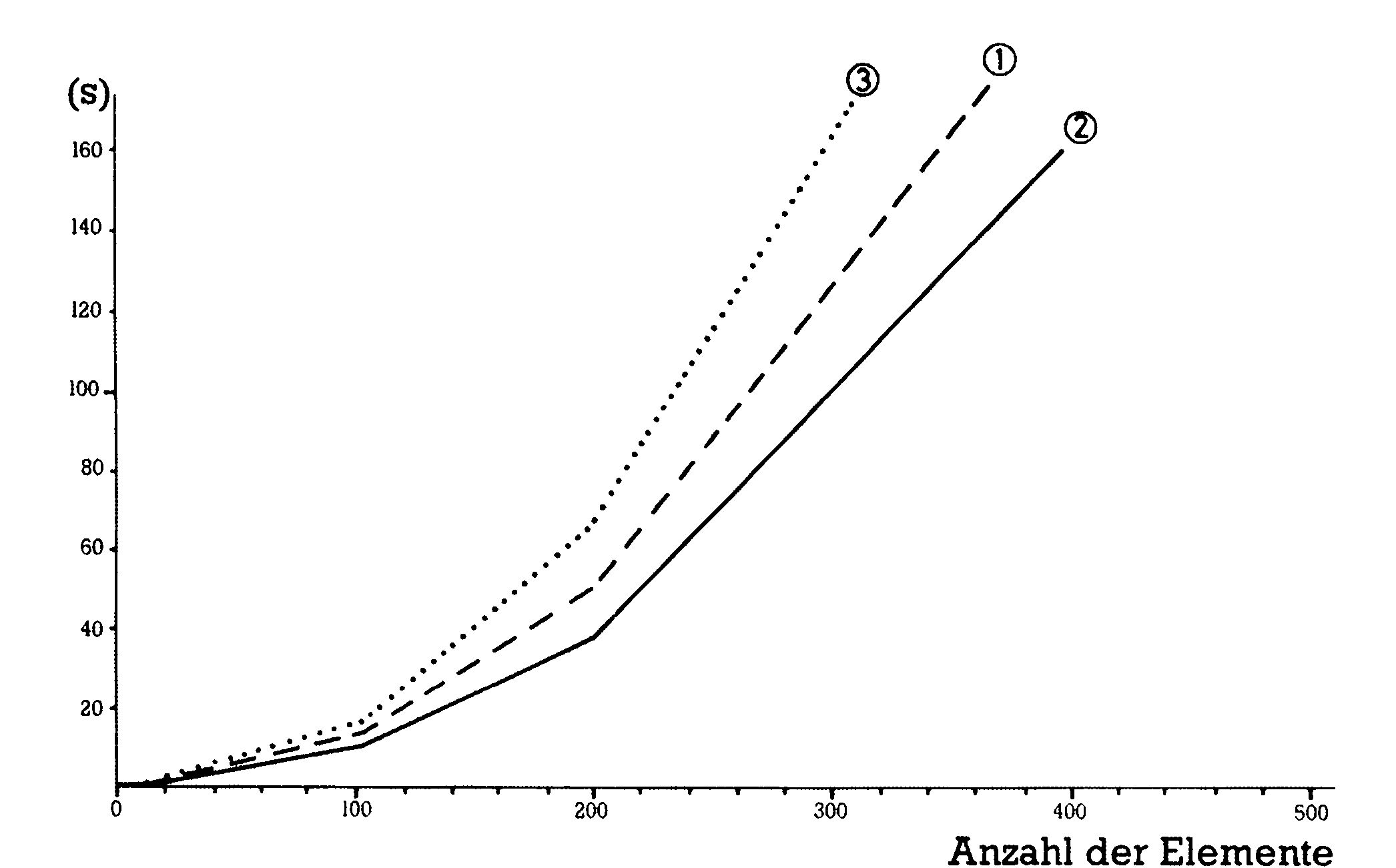
Bild 8 zeigt uns den ersten effektiven Algorithmus, der durchaus schon praktisch eingesetzt werden kann. Es handelt sich um Shellsort, und wir können unschwer erkennen, daß diese Kurve im Gegensatz zu der von Straight Selection schon ziemlich flach verläuft, was einen langsameren Anstieg der Sortierzeiten bei steigender Anzahl von Elementen zur Folge hat.

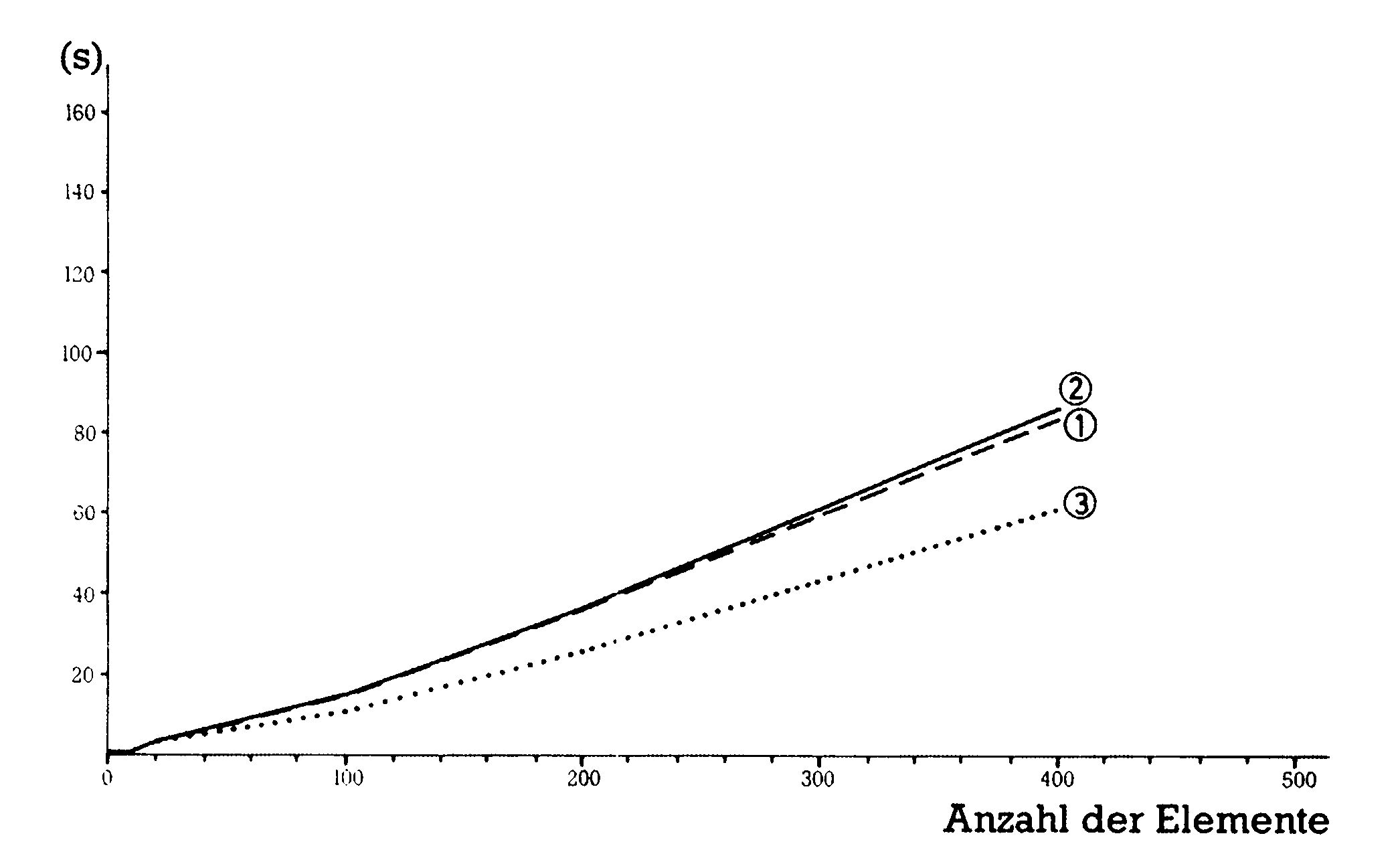
Die Kurve in Bild 9 hat einen ganz ähnlichen Verlauf zur Kurve in Bild 8, nur ist die Steigung wieder um ein Stück flacher geworden. Heapsort läßt also durchaus auch praktische Anwendungen zu, es wird jedoch wegen seiner komplizierten Struktur kaum eingesetzt.

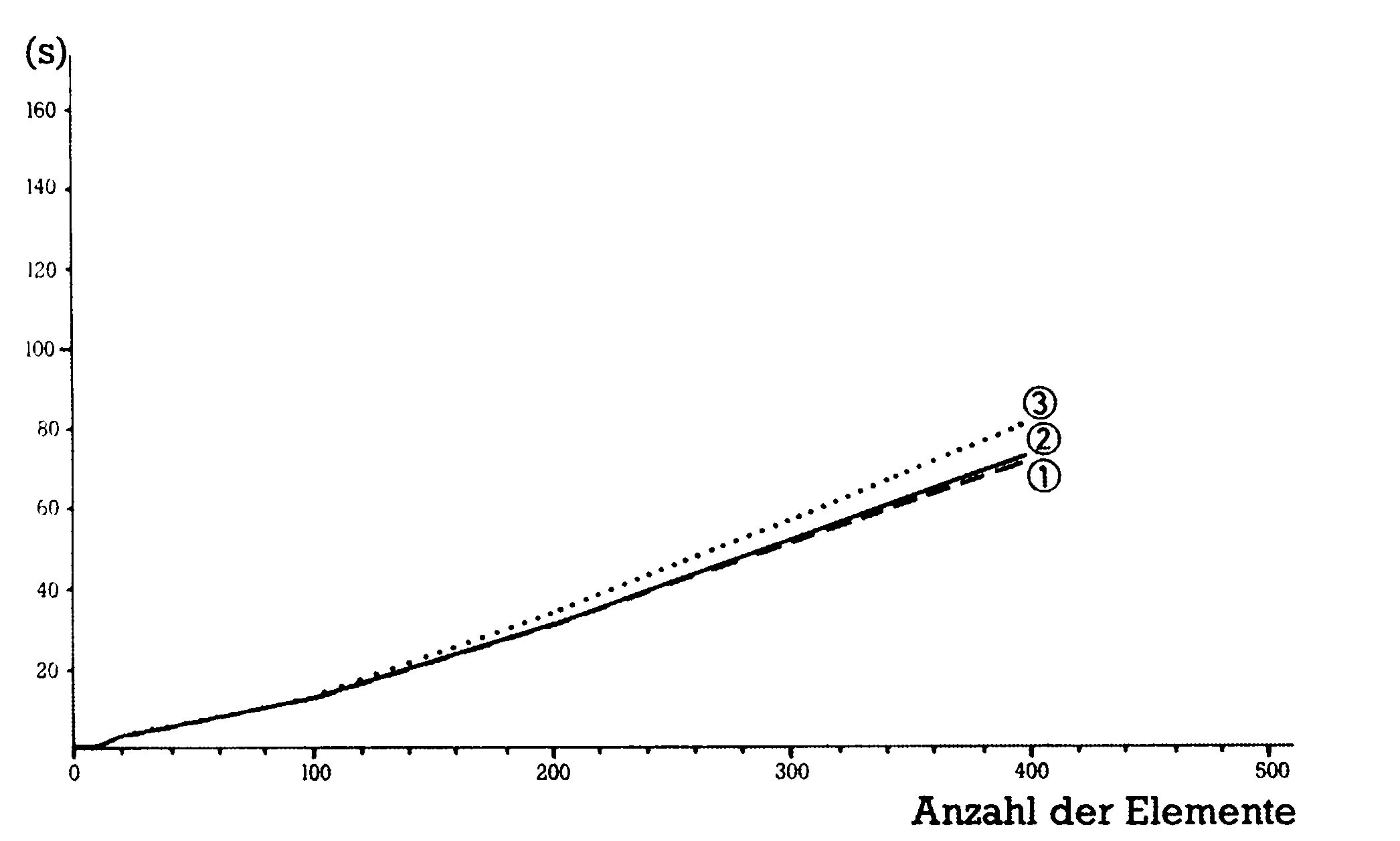
Bild 10 zeigt den Zeitverlauf bei Quicksort. Das Erstaunliche an den höheren Sortieralgorithmen ist, daß sich alle Sortierzeiten, sowohl die von völlig unsortierten Feldern als auch die von sortierten Feldern ständig aneinander annähern, was auf einen sehr breit gefächerten Anwendungskreis dieser Sortiermethoden schließen läßt.

Eine Sache sollte im Zusammenhang von Quicksort nicht unerwähnt bleiben: Supersort bedient sich Bubblesort zur Endsortierung seiner Teilfelder. Diese Methode ist auch bei Quicksort üblich, wenngleich wir das in unserem Kurs nicht berücksichtigt haben. Es zeigt sich nämlich in der Praxis, daß die »großen« Sortiermethoden bei kleiner werdenden Teilfeldern mitunter sehr schwerfällig arbeiten, weshalb es besser ist, diese Teilfelder (zirka 10 Elemente) an kleine (und bei diesen Größen auch schnelle) Sortieralgorithmen zu übergeben.

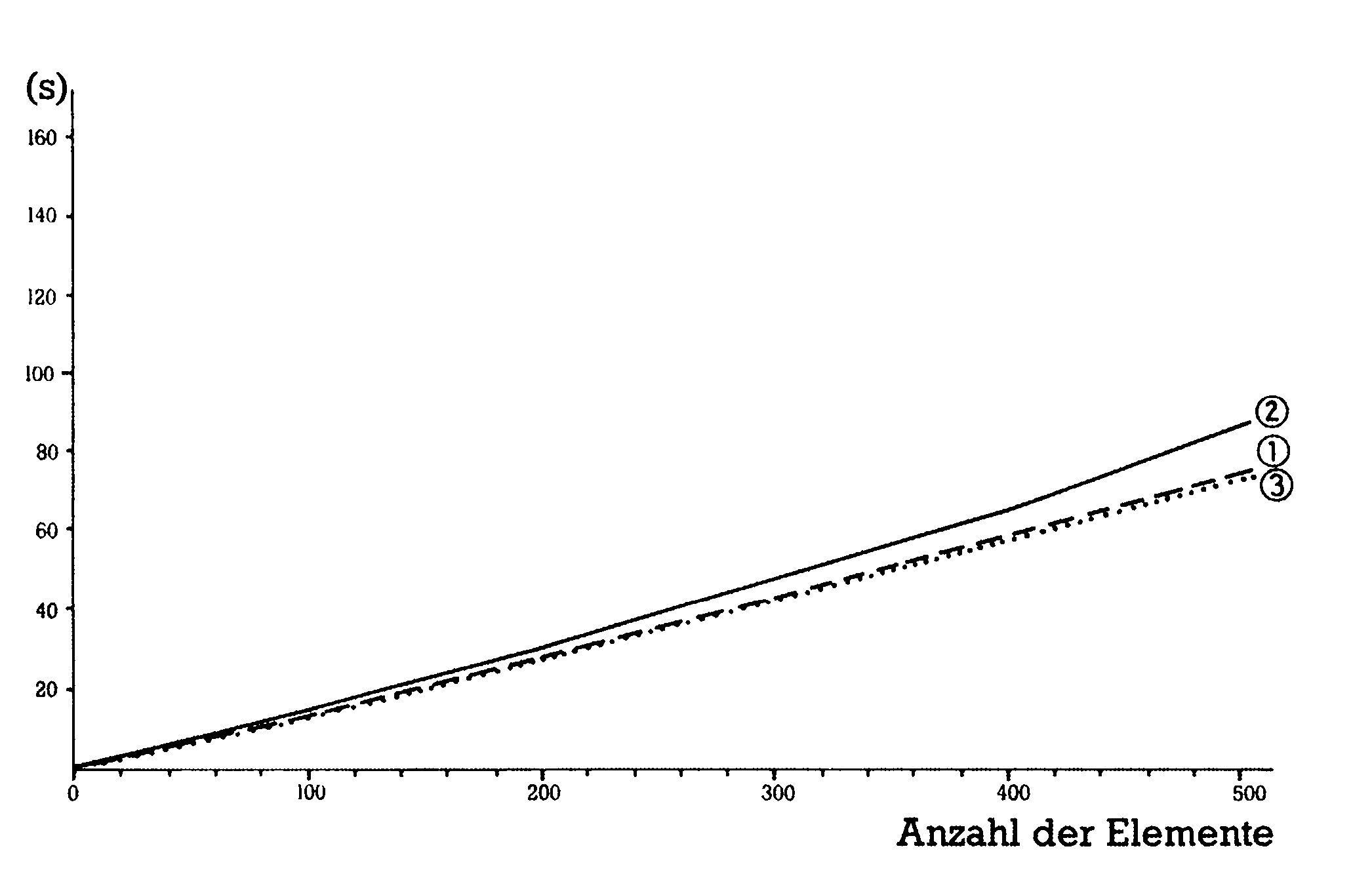
Bild 11 macht uns mit der Geschwindigkeit von Supersort vertraut und bringt schon die erste Überraschung:

Bei unsortierten Feldern bis zu 400 Elementen und bei aufwärts sortierten ist der Sortieralgorithmus schneller als Quicksort, bei abwärts sortierten langsamer. Außerdem zeigte sich Supersort im Test wenig entgegenkommend, was seine Zuverlässigkeit betrifft.

Erstens baut Supersort seine Teilfelder mit Hilfe einer Stringvariable auf, die bekanntermaßen nur 255 Zeichen lang werden kann. Das hat den Haken, daß Supersort mit einer »?STRING TOO LONG«-Meldung ausstieg, sobald eine ganze Reihe von gleichartigen Elementen verarbeitet werden mußten. Das ist jedoch bei einem vorsortierten Feld leider oft der Fall. Aus diesem Grund mußte ich bei einer Zahl ab 100 sortierten Elementen mit dem Test aufhören.

Zweitens fiel bei Supersort unangenehm auf, daß diese Sortierroutine nicht in der Lage ist, Strings zu sortieren, die Zahlen enthalten, was auf die Beschränkung auf 26 Zeichen des Alphabets zurückzuführen ist.

Hätte Supersort, abgesehen von den obigen Schwächen, einwandfrei gearbeitet, so hätte man sicher auf interessante Meßwerte kommen können. Es zeigte sich jedoch schon bei den zufallssortierten Elementen, daß Supersort auf ganz andere Schwierigkeiten stößt, wenn die Zahl der Elemente über 500 hinaus geht. Auch hier wieder das berüchtigte Wort Garbage Collection. Supersort benötigt nämlich mehr Zwischenspeicher als Quicksort und wird somit von diesem überholt, sobald bei Supersort die Garbage Collection in Aktion tritt (und das tut sie natürlich früher als bei Quicksort).

Natürlich kann man jetzt den Entwickler dieses Programms nicht des Lügens bezichtigen, wenn er behauptet: »Supersort ist schneller als Quicksort!«. Supersort ist nämlich ursprünglich auf einem CBM 8032 geschrieben worden, und dieser verfügt über eine andere Stringverwaltung als der C 64, was eine erheblich schnellere Garbage Collection zur Folge hat

Für den C 64 gilt jedoch (leider): Supersort ist nur bedingt brauchbar, da es einige Schwächen aufweist, die Quicksort nicht hat.

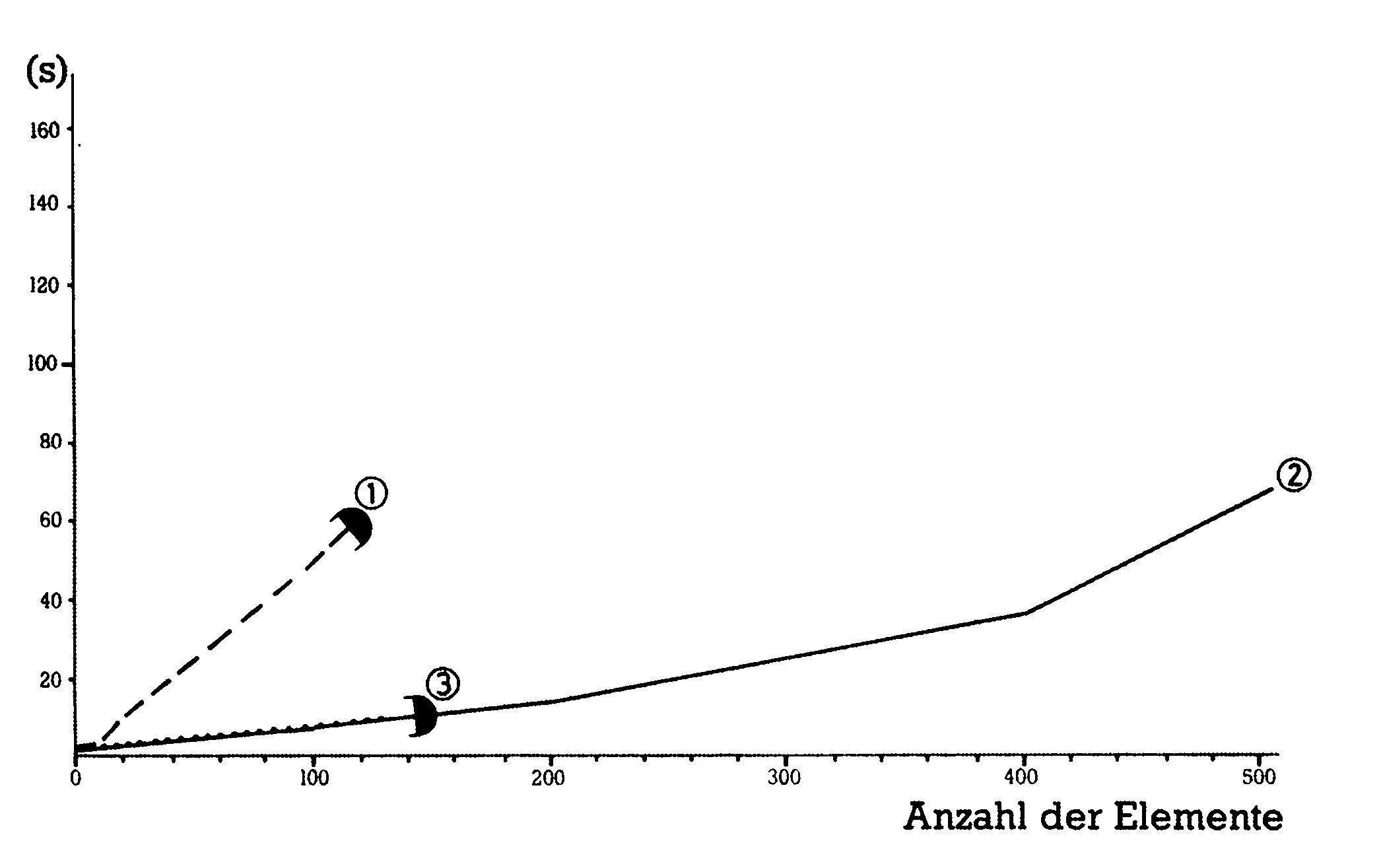
Nun zu Bild 12. Es zeigt den letzten der Sortieralgorithmen, nämlich Mischsort. Und hier erlebte ich die große Überraschung: Auch Mischsort ist schneller als die Normalversion von Quicksort (ohne Tricks mit kleineren Sortierroutinen). Mischsort zeigte im Test wahrhaftig traumhafte Zeiten für Basic-Sortierprogramme, die teilweise nur 50 Prozent der Zeiten von Quicksort betrugen. Es wurde auch deutlich, daß bei Mischsort die Garbage Collection noch später einsetzte als bei Quicksort (das Einsetzen der Garbage Collection ist an den »Knickstellen« der Graphen zu erkennen), was die guten Zeiten aber nur teilweise rechtfertigte.

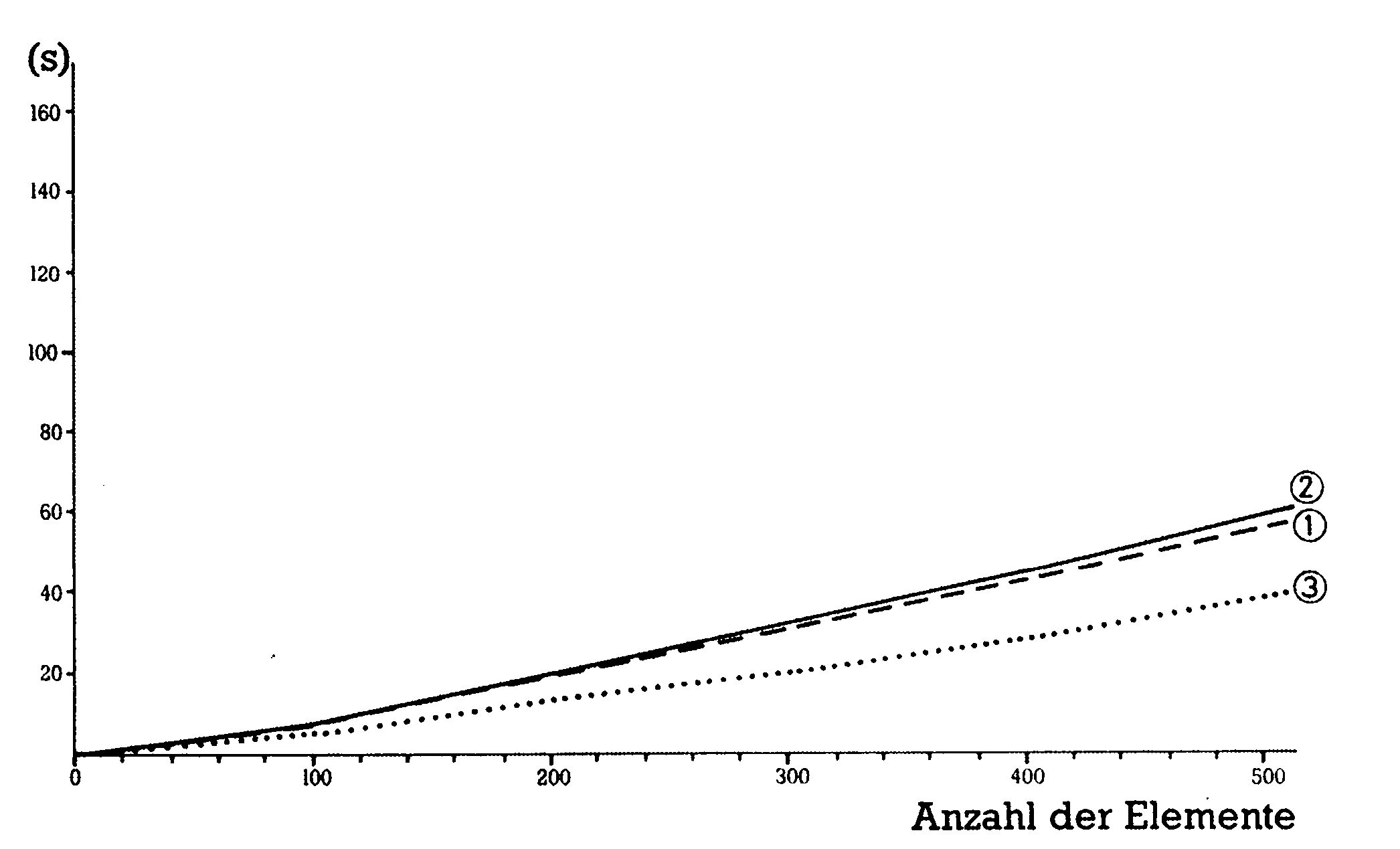
Mischsort ist genauso einsatzfähig wie Quicksort (ohne »Macken«) und kann deshalb als bestes Sortierprogramm dieses Tests betrachtet werden. Haben Sie viele große Felder zu sortieren, so spielt es bei diesem Algorithmus fast keine Rolle, ob die Felder vorsortiert sind oder nicht; schnell ist er auf jeden Fall.

Noch eine Randbemerkung zum Schluß: Vielleicht haben Sie auch schon Methoden entwickelt, wie sie die Garbage Collection »in den Griff bekommen«. Haben Sie vielleicht als »Maschinensprachefreak« ein neues Basic-ROM geschrieben (mit besserer Stringverwaltung) oder haben Sie anhand unseres Vorkurses über Strings die Lösung des Problems gefunden?

Die 64’er-Redaktion würde sich über Beiträge aus dem Leserkreis freuen. Vielleicht möchten Sie dazu beitragen, daß auch andere Anwender in den Genuß entsprechender Verbesserungen kommen?

Schreiben Sie uns doch! Bestimmt können wir dann den einen oder anderen Trick mit in unsere Reihe aufnehmen.

Bis zum nächsten Mal.