Sortieren mit Computer (Teil 6)
Wie werden Sortierroutinen schneller? Wie kann die Garbage Collection verhindert werden? Wir beschreiben einige Verfahren dazu und bringen Quicksort in Maschinensprache.
Im letzten Teil unseres Sortierkurses sollen einmal Techniken erläutert werden, die die bisher besprochenen Sortieralgorithmen noch effektiver werden lassen. Außerdem werden wir auf die wichtigsten der vielen Leserreaktionen eingehen und etwaige Mißverständnisse und Fehler aus dem Weg räumen.
Die wichtigsten Sortieralgorithmen wurden in unserem Kurs ausführlich besprochen, wobei wir bisher jedoch recht wenig auf Programmiertechniken eingegangen sind, die unseren Programmen zu noch größeren Geschwindigkeiten verhelfen. Zwei Methoden seien an dieser Stelle schon einmal erwähnt:
- das Umschreiben der Sortieralgorithmen in Maschinensprache;
- das Verhindern der Garbage Collection durch Sortieren der String-Deskriptoren, wobei kein »Stringmüll« entsteht.
Leserreaktionen
Bevor wir uns jedoch auf die gestellten Probleme stürzen, möchte ich mich bei all jenen Lesern bedanken, die mir zu diesem Thema geschrieben haben. Wir machen ohnehin kein Geheimnis daraus, daß die Zeitschrift 64’er zu einem erheblichen Teil von der Mitarbeit aktiver Leser geprägt wird, und wir hoffen, daß das auch in Zukunft so bleibt.
Nun aber zu einigen wichtigen Informationen.
Ziemlich viel Rummel hat offensichtlich die Ankündigung von Sortieralgorithmen hervorgerufen, die schneller sein wollen als Quicksort.
Es kamen prompt Zuschriften von Lesern, die diese Behauptung mit den eingesendeten Quicksort-Algorithmen widerlegen konnten. Der Trick bei der Sache war ausschließlich auf ein System zurückzuführen, das ein Feld von Quicksort nur teilsortieren läßt und die Arbeit bei einer Teillistenlänge von beispielsweise 10 an ein »kleines« Sortierprogramm (Bubblesort 2 oder Straight Insertion) übergibt. Diese Methode ist natürlich korrekt! Es wurde in dem Kurs jedoch absichtlich vom Abdruck eines solchen Sortieralgorithmus abgesehen, weil es bei den Beispielprogrammen einzig und allein um die Struktur der großen Sortieralgorithmen ging. Auf die oben beschriebene Methode zum »Schnellermachen« von Quicksort (und auch Heapsort) hatte ich aber an anderer Stelle schon hingewiesen.
Quicksort ist doch am schnellsten
Ein sehr wichtiger Brief kam jedoch von unserem Leser Kurt Sörensen aus Hamburg. Er zeigte nämlich einen Fehler auf, der in der abgedruckten Beispielroutine von Quicksort steckt (Achtung Fehlerteufelchen…). Herr Sörensen analysierte das Quicksortprogramm und kam zu folgendem Ergebnis:
»… Beim Übergang von der linken zur rechten Hälfte wird die rechte Grenze der linken Hälfte, die nach der Theorie schon sortiert ist, zur linken Grenze der rechten Hälfte gemacht, die nach der Theorie noch nicht sortiert ist. Dadurch werden praktisch alle Elemente außer dem kleinsten und dem größten doppelt sortiert…«
Wie Sie aus unserem Kurs wissen, teilt Quicksort während des Sortierens das Variablenfeld in immer kleiner werdende Hälften (Teillisten) auf. Berücksichtigt man also diesen Fehler und erstellt das Quicksortprogramm neu (nach wie vor ohne anschließenden anderen Algorithmus), so kann sich Quicksort wieder unbeschadet an die Spitze unserer Stringsortierroutinen stellen. Es ist und bleibt der schnellste (und dabei der vielseitigste) Sortieralgorithmus (»Sonderanfertigungen« für spezielle Probleme laufen natürlich außer Konkurrenz!)
In Listing 1 sehen Sie die korrigierte Version von Quicksort abgedruckt.
Nun zu einem Problem, das offensichtlich in Zusammenhang mit unserem Hauptprogramm für die Sortieralgorithmen aufgetreten ist. Wie Sie wissen, haben wir zu den entsprechenden Sortierprogrammen auch ein Hauptprogramm abgedruckt, das einen Test der einzelnen Routinen ermöglichen sollte. Der Sinn dieses Programms ist aber von mir offensichtlich nicht genug verdeutlicht worden.
Bei dem beigefügten Rahmenprogramm handelt es sich um ein provisorisches Gerüst, das es dem Leser erlauben soll, die eingegebenen Sortierprogramme auf Funktionsfähigkeit und Geschwindigkeit zu testen. Daß das Rahmenprogramm also kein »Z« als Zufallswert verarbeitet und außerdem nur Elementzahlen in Zehnersprüngen zuläßt, dürfte bei der Arbeit kaum ein Hindernis darstellen, zumal das ja der Sinn der Sortierroutinen ist, nach Fertigstellung in andere Programme eingefügt zu werden. Im eigentlichen Sinne wichtig für den Anwender sind also jeweils die Programmteile in den Zeilen 10 000 bis 20 000: Der Rest entfällt.
Nun aber zu den schon erwähnten Programmiertechniken, die der Beschleunigung eines Sortiervorgangs dienen.
Es geht noch schneller
Wir wollen uns dazu zuerst mit einem Artikel in der 64’er, Ausgabe 1/1985 beschäftigen. Es handelt sich hierbei um die erste Ausgabe in der Reihe »Effektives Programmieren«, die damals von dem Stringspezialisten Boris Schneider geschrieben wurde. Vorherrschend ging es um ein Problem bei der Stringverwaltung, nämlich um die »Müllabfuhr im Computer«, die Garbage Collection. Damals wurde sehr ausführlich auf den Aufbau von Strings im Speicher des Computers eingegangen, weshalb an dieser Stelle nur eine sehr knappe Wiederholung folgen soll.
Generell legt der C 64 seine Variablen direkt im Anschluß an das Basic-Programm im Speicher ab. Auch die Stringvariablen stehen dort. Der Textinhalt dieser Variablen wird jedoch an anderer Stelle im Speicher, nämlich von oben anfangend, rückwärts nach unten gespeichert. Anstelle des Textes hinter dem Variablennamen wird dort ein Zeiger (Deskriptor) abgelegt, der auf die jeweilige Position des Textes zeigt.
Wird nun eine Stringvariable neu angelegt, nachdem sie zuvor einen anderen Inhalt aufwies, wird der neue Text an die Stringkette im oberen Speicherbereich angehängt und der Deskriptor der Variablen auf diesen neuen Text eingestellt. Der »alte« Variablentext bleibt im Speicher stehen und bildet »Stringmüll«. Dieser Müll steigt mit vielen Neudefinitionen von Strings rapide an, so daß es nur eine Frage der Zeit ist, wann die von oben kommenden Strings mit den von unten kommenden Variablen zusammenstoßen und einen »?OUT OF MEMORY ER-ROR« verursachen.
Um diesem Fehler vorzubeugen, gibt es die Garbage Collection. Der Interpreter überwacht laufend den Zustand des Speichers. Wird es zu eng, dann tritt die Garbage Collection in Kraft und räumt den gesamten Stringmüll weg. Dieser Vorgang erfordert enorme Speichersuch- und verschiebevorgänge und kann ungünstigenfalls sogar mehrere Stunden benötigen: Der Computer scheint »abgestürzt«.
Bei unseren Sortiervorgängen wird ziemlich häufig der sogenannte Dreiecktausch durchgeführt. Es handelt sich hierbei um das Vertauschen der Inhalte von zwei Stringvariablen, wobei eine dritte Variable als Zwischenspeicher dient: zum Beispiel:
x$ = a$(1):a$(1) = a$(2):a$(2) = x$
Bei diesem Tauschverfahren werden gleich drei Müllstrings erzeugt, nämlich der Inhalt von x$, der alte Inhalt von a$(1) und der alte Inhalt von a$(2).
Nun gibt es Basic-Interpreter, die bieten zu diesem Zweck den Befehl SWAP an. Mit diesem Befehl können die Inhalte zweier Strings direkt vertauscht werden. Zum Beispiel:
SWAP a$(1), a$(2)
Hiermit sparen wir Zeit und Speicherplatz. Zeit sparen wir durch die Ausführung eines einzigen Befehls anstatt der drei Variablenzuordnungen. Speicherplatz sparen wir durch das Wegfallen der Hilfsvariable x$, so daß nur zwei Müllstrings entstehen.
SWAP - ein Programm mit Pfiff
Aber pingelig, wie wir Computermenschen nun einmal sind, stellt uns auch diese Methode nicht zufrieden. Hatten wir vorhin nicht etwas von Deskriptoren, also von Zeigern auf den jeweiligen String gehört? Genau! Das ist unser neuer Ansatzpunkt!
Bei dem Vertauschen von zwei Variablen ändert sich nämlich eigentlich gar nichts im Speicher. Es bleiben sowohl die beiden Strings als auch die beiden Variablennamen erhalten. Warum reicht es also nicht aus, einfach die beiden Stringdeskriptoren zu vertauschen? Diese Frage ist überflüssig! Es reicht nämlich in der Tat aus, wenn wir den Deskriptor von Variable 1 auf den String von Variable 2 und umgekehrt setzen.
Und genau das macht das Programm SWAP, das Boris Schneider schon in der 64’er, Ausgabe 1/1985, Seite 123 vorgestellt hat.
Mit Hilfe dieser kleinen Maschinenspracheroutine sparen wir also Zeit und Stringmüll, da kein einziger überflüssiger String entsteht (Listing 2). Wenn Sie das »Progrämmchen« eingetippt haben, dann starten Sie es mit RUN. Sie werden anschließend nach der Startadresse des Maschinenprogramms gefragt. Diese sollten Sie vorzugsweise in den $C-Bereich (49152 bis 53247) legen, wobei darauf zu achten ist, daß als Startadresse maximal 53199 gelten darf (Das Programm benötigt 48 Byte).
Muß die Routine aus irgendeinem Grund woanders untergebracht werden, so wäre noch der Kassettenpuffer (828 bis 1023) zu empfehlen, um Basic-Speicherplatz zu sparen. Andernfalls müssen Sie eben die maximale Speicheradresse entsprechend heruntersetzen, um die Swap-Routine vor dem Überschreiben mit Strings zu schützen. Der Einbau des SWAP in die Sortierprogramme ist vollkommen unproblematisch. Sie suchen sich einfach jeweils die Stelle mit dem Dreiecktausch heraus. Sie wird in den abgedruckten Sortierprogrammen durch die Variable S$ als Hilfsvariable gekennzeichnet. Bei Straight Select ist das beispielsweise die Zeile 10080:
10080 S$ = A$(X):A$(X) = A$(Z): A$(Z) = S$
Diese Zeile wird nun wie folgt geändert:
10080 SYS startadresse(A$(X), A$(Z))
»startadresse« gibt hierbei die Zahl an, die Sie beim Start des SWAP-Programms angegeben hatten. Die abgeänderte Version von Straight Select zeigt Listing 3. Sinnvoll wäre es, die SWAP-Routine direkt vor unser Sortier-Hauptprogramm zu setzen, so daß sie immer direkt vor dem Arbeiten automatisch installiert wird.
Von der Speicherplatzersparnis einmal ganz abgesehen, arbeitet auch diese SWAP-Routine schon erheblich schneller als der Dreiecktausch, so daß zum Beispiel beim Sortieren von 100 Elementen mit Bubblesort2 aus einer Sortierzeit von 1 Minute 46 Sekunden »nur« 1 Minute und 33 Sekunden wurden. Besonders bei sehr großen Elementzahlen zeigt sich aber dann die Effizienz dieses Programms, da sich die Garbage Collection kaum mehr blicken läßt. Unser Quicksort erfährt dadurch wiederum neue Bestzeiten im Sortieren von zufallsbesetzten Feldern.
Es geht doch nichts über Maschinensprache
Wem aber auch dieser Trick noch nicht reicht: Wer immer noch auf der Suche nach dem »HYPRA« ist, dem bleibt nichts anderes übrig, als auf der Maschinenspracheebene sein Glück zu versuchen.
Mit diesem Thema hat sich auch unser Leser Frank Probst aus Zweibrücken beschäftigt. Was dabei herausgekommen ist, wollen wir Ihnen jetzt vorstellen: Quicksort in Maschinensprache!
Es war natürlich von vornherein klar, daß wirklich gute Zeiten beim Sortieren von Feldern nur in Maschinensprache zu erreichen sind. Wenn man jedoch das Prinzip eines Sortieralgorithmus verstehen will, ist es in der Regel besser, sein Glück erst einmal in Basic zu versuchen und das erworbene Wissen dann in Maschinensprache umzusetzen.
Quicksort in Maschinensprache!
Da Quicksort ja nun schon in Basic am schnellsten ist und erstaunliche Sortierzeiten hervorbringt, darf man auf die Maschinenpracheversion gespannt sein. Ich kann schon vorwegnehmen, daß dieses Programm (natürlich) alles bisher Dagewesene voll in den Schatten stellt. Bevor wir uns jedoch diesem Programm zuwenden, soll an dieser Stelle erwähnt sein, daß durchaus nicht alle Tricks, die der Geschwindigkeit von Nutzen sein könnten, angewendet wurden. So teilt dieses Quicksort alle Teillisten bis auf die Länge 1 herunter, anstatt bei zum Beispiel 10 aufzuhören und dann Straight Select ans Werk zu lassen. Die Methode des Deskriptortausches wurde jedoch auch hier angewendet, was zur Folge hat, daß die Garbage Collection so gut wie keine Arbeit bekommt (selbst wenn große Mengen an Daten sortiert werden müssen).
Die Bedienung von Quicksort-M (so möchte ich es für den weiteren Verlauf nennen, um es von der Basic-Version zu unterscheiden) ist denkbar einfach. Nachdem Sie das Listing 4 mit dem MSE eingetippt und auf Diskette gespeichert haben, steht Quicksort-M sofort zur Verfügung. Es belegt im Speicher den Bereich von $CB20 bis $CFFF und verträgt sich so mit einem eventuell eingeschalteten Turbo-Tape. Es wird mit SYS52000 aufgerufen, wobei jedoch einige Regeln zu beachten sind:
Das zu sortierende Feld muß ein Stringarray sein und als allererstes Feld in einem Programm dimensioniert werden. Andernfalls kann ein »Aussteigen« des Computers die Folge sein. Bei der Arbeit benötigt Quicksort-M die Speicherstellen von $00B2-$00B8 und $00FB-$00FE. Die Werte aus $00B2 bis $00B8 werden gerettet und nach der Sortierung wieder zurückgeschrieben.
Das eigentliche Quicksort-M-Programm belegt nur die Speicherstellen $CB20 bis $CDE7. Es benötigt jedoch den anschließenden Bereich als Speicher für den jeweiligen Vergleichsstring und für einen Software-Stack, der bei Quicksort ja generell notwendig ist.
Wer sich mit Quicksort-M weiter beschäftigen will, der findet in Listing 5 ein Source-Listing.
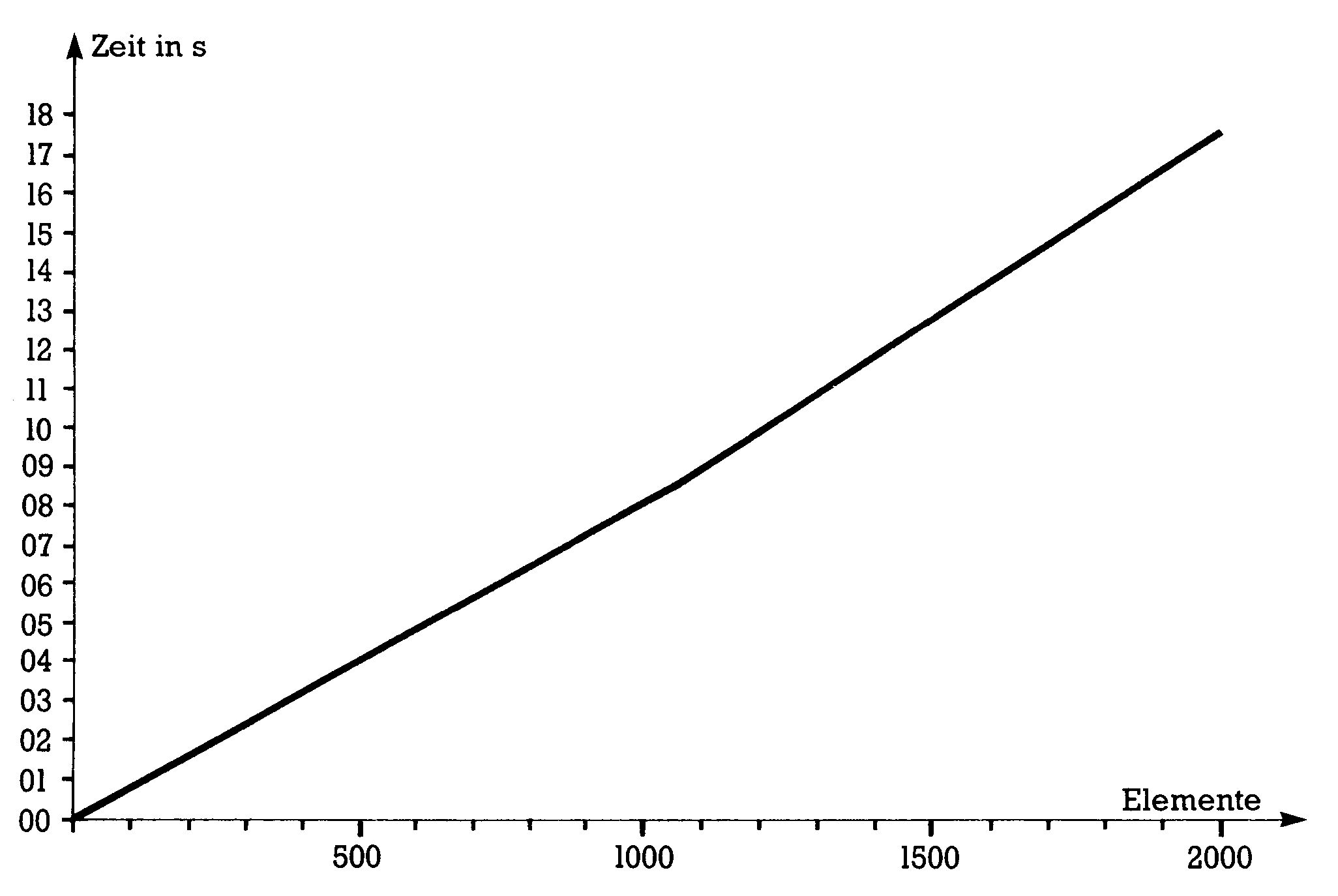
Nun aber zu den Daten von Quicksort-M. Hier erübrigt sich jeder weitere Kommentar, wenn Sie sich Bild 1 betrachten. Diese Zeiten wurden mit dem Basic-Programm Quicktester (Listing 6) ermittelt und lassen einen das Schwärmen anfangen. Quicksort-M benötigt beispielsweise für 1 000 zufällig ausgewählte Elemente nur noch acht Sekunden (!). Diese Zeit dürfte sich dabei auf ein Maß beschränken, das auch den pingeligsten Anwender des C 64 zufriedenstellen dürfte. Immerhin schlägt Quicksort-M seine Basic‑Konkurrenten alle um einige 1 000 Prozent: Sogar das »normale« Quicksort wird hier haushoch geschlagen.
Ursprünglich hatte ich vor, an dieser Stelle auch noch einen Bubblesort-Algorithmus in Maschinensprache vorzustellen. Doch was brauchen wir jetzt noch Bubblesort? Quicksort-M dürfte, was die Geschwindigkeit angeht, wohl allen Anwendungen gewachsen sein. Wer sich dennoch mit Bubblesort auseinandersetzen will, der findet in einer anderen Zeitschrift aus dem Markt & Technik-Verlag einen Beitrag zu diesem Thema: Er steht unter dem Titel »Schneller als Quicksort« und erschien in der Ausgabe 14/1985 des Magazins Computer persönlich. Weitere Sortierprogramme finden Sie in Computer persönlich, Ausgabe 14/1984 (Top-Sort) und im 64’er, Ausgabe 11/84 (Exsort), ebenfalls als Maschinenprogramm.
Ich möchte mich an dieser Stelle von Ihnen verabschieden und hoffe, daß Ihnen die letzten Kurse ein wenig Spaß gemacht haben. Vielleicht haben Sie jetzt das Werkzeug, um sich das eine oder andere Projekt, das Sie sich schon länger vorgenommen hatten, zu verwirklichen.
(K. Schramm/F. Probst/gk)10000 rem quicksort 10010 : 10020 t=ti:lg(1)=1:rg(1)=a:z=0:gosub 10040 10030 return 10040 z=z+1:if lg(z)>=rg(z) then 10170 10050 x=lg(z):y=rg(z):if y<=x+1 goto 10170 10060 b=(x+y)/2:b=int(b):vg$=a$(b) 10070 if x>y then 10150 10080 if a$(x)<vg$then x=x+1:goto 10080 10090 if a$(y)>vg$then y=y-1:goto 10090 10100 if x>y then 10150 10110 s$=a$(x):a$(x)=a$(y):a$(y)=s$ 10120 x=x+1:y=y-1:goto 10070 10130 if a$(x)<=a$(y)goto 10170 10140 s$=a$(x):a$(x)=a$(y):a$(y)=s$:goto 10170 10150 rg(z+1)=y:lg(z+1)=lg(z):gosub 10040 10160 lg(z+1)=rg(z+1)+1:rg(z+1)=rg(z):gosub 10040 10170 z=z-1:return
10 data32,250,174,32,158,173,32,143 20 data173,165,100,133,247,165,101,133 30 data248,32,253,174,32,158,173,32 40 data143,173,160,0,177,247,133,249 50 data177,100,145,247,165,249,145,100 60 data200,192,3,208,239,32,247,174 70 data96,0,0,0,0,0,0,0 100 input"startadresse";sa 110 fori=sa to sa +48 120 readx:pokei,x:cs=cs+x 130 next i 140 if cs<>7314 then print"fehler!!" 150 end
10040 ti$="000000":g=a-1:forx=a-1to1step-1 10050 f=0:fory=1tog 10060 ifa$(y)<=a$(y+1)then10080 10070 f=y:sys49152(a$(y),a$(y+1)) 10080 nexty 10090 g=f:iff=0then50000 10100 nextx
PROGRAMM : QUICKSORT.OBJ CB20 CDE8 ----------------------------------- CB20 : 20 E0 CC A2 00 B5 B2 9D EB CB28 : BC 02 E8 E0 06 D0 F6 20 3E CB30 : 3F CB A2 00 BD BC 02 95 F2 CB38 : B2 E8 E0 06 D0 F6 60 20 DE CB40 : 03 CC 20 B6 CD 20 EE CB B9 CB48 : C9 00 F0 58 C9 02 F0 54 72 CB50 : 20 A8 CD 20 30 CD 20 D3 D5 CB58 : CB C9 02 F0 3B 20 1A CD 5F CB60 : 20 A7 CB C9 02 F0 0A C9 E3 CB68 : 00 F0 06 20 27 CC 4C 5D 2B CB70 : CB 20 20 CD 20 A7 CB C9 0F CB78 : 01 F0 0A C9 00 F0 06 20 8D CB80 : 39 CC 4C 71 CB 20 D3 CB 05 CB88 : C9 02 F0 0C 20 A8 CC 20 CB CB90 : 27 CC 20 39 CC 4C 56 CB 6D CB98 : 20 8B CD 20 3F CB 20 6E A5 CBA0 : CD 20 3F CB 4C 15 CC A0 A8 CBA8 : FF C8 C4 B2 D0 05 A9 01 71 CBB0 : 4C CA CB C4 B5 D0 05 A9 36 CBB8 : 02 4C CA CB B1 B3 D1 B6 7A CBC0 : F0 E7 90 03 A9 02 2C A9 D7 CBC8 : 01 60 A6 B2 E4 B5 D0 02 3C CBD0 : A9 00 60 AD EA CD CD EC 75 CBD8 : CD D0 08 AD E9 CD CD EB E1 CBE0 : CD F0 05 B0 06 A9 01 2C 87 CBE8 : A9 00 2C A9 02 60 AD F0 8D CBF0 : CD CD F2 CD D0 08 AD EF FE CBF8 : CD CD F1 CD F0 EA B0 EB E3 CC00 : A9 01 60 18 AD E7 CD 69 69 CC08 : 04 8D E7 CD AD E8 CD 69 B2 CC10 : 00 8D E8 CD 60 38 AD E7 19 CC18 : CD E9 04 8D E7 CD AD E8 02 CC20 : CD E9 00 8D E8 CD 60 18 42 CC28 : AD E9 CD 69 01 8D E9 CD 2A CC30 : AD EA CD 69 00 8D EA CD A7 CC38 : 60 38 AD EB CD E9 01 8D E8 CC40 : EB CD AD EC CD E9 00 8D 62 CC48 : EC CD 60 AD E9 CD 0A AA 73 CC50 : AD EA CD 20 8D CC 6D E9 B2 CC58 : CD AA 98 6D EA CD 4C 92 C1 CC60 : CC AD EB CD 0A AA AD EC 3E CC68 : CD 20 8D CC 6D EB CD AA 05 CC70 : 98 6D EC CD 4C 92 CC AD 9B CC78 : ED CD 0A AA AD EE CD 20 ED CC80 : 8D CC 6D ED CD AA 98 6D FC CC88 : EE CD 4C 92 CC 2A A8 8A 98 CC90 : 18 60 A8 18 8A 69 07 AA 6B CC98 : 98 69 00 A8 18 8A 65 2F C4 CCA0 : 85 FB 98 65 30 85 FC 60 D9 CCA8 : 20 4B CC A5 FB 85 FD A5 85 CCB0 : FC 85 FE 20 61 CC A0 00 31 CCB8 : B1 FB AA B1 FD 91 FB 8A B9 CCC0 : 91 FD C8 C0 03 D0 F1 60 D9 CCC8 : 18 AD E9 CD 6D EB CD 8D 73 CCD0 : ED CD AD EA CD 6D EC CD 04 CCD8 : 4A 8D EE CD 6E ED CD 60 AC CCE0 : A9 00 8D E9 CD 8D EA CD BA CCE8 : A9 07 8D E7 CD A9 CE 8D F6 CCF0 : E8 CD 20 4B CC EE E9 CD B8 CCF8 : 38 A5 FB E9 02 85 FB A5 C6 CD00 : FC E9 00 85 FC A0 01 38 EB CD08 : B1 FB E9 01 8D EB CD 88 D2 CD10 : B1 FB E9 00 8D EC CD 4C 49 CD18 : D7 CD 20 4B CC 4C 23 CD 9F CD20 : 20 61 CC A0 00 B1 FB 99 E9 CD28 : B2 00 C8 C0 03 D0 F6 60 78 CD30 : 20 C8 CC 20 77 CC A0 00 4C CD38 : B1 FB 99 B5 00 C8 C0 03 53 CD40 : D0 F6 A5 B5 F0 1C C9 15 ED CD48 : 90 04 A9 14 85 B5 A0 00 50 CD50 : B1 B6 99 F3 CD C8 C4 B5 E3 CD58 : D0 F6 A9 F3 85 B6 A9 CD DC CD60 : 85 B7 60 AD E7 CD 85 FD 8E CD68 : AD E8 CD 85 FE 60 20 B6 8E CD70 : CD 20 C6 CD A0 00 B9 E9 7D CD78 : CD 91 FD C8 C0 02 D0 F6 F3 CD80 : B9 EF CD 91 FD C8 C0 04 07 CD88 : D0 F6 60 20 B6 CD 20 C6 D7 CD90 : CD A0 00 B9 EF CD 91 FD 94 CD98 : C8 C0 02 D0 F6 B9 E9 CD DB CDA0 : 91 FD C8 C0 04 D0 F6 60 DD CDA8 : A0 00 B9 EF CD 99 E9 CD A1 CDB0 : C8 C0 04 D0 F5 60 20 63 9D CDB8 : CD A0 00 B1 FD 99 EF CD 14 CDC0 : C8 C0 04 D0 F6 60 20 63 BD CDC8 : CD 18 A5 FD 69 04 85 FD 93 CDD0 : A5 FE 69 00 85 FE 60 20 61 CDD8 : C6 CD A0 00 B9 E9 CD 91 F2 CDE0 : FD C8 C0 04 D0 F6 60 20 78
10 SYS36864:.OPT P,OO:*= 52000 20 LAENGE1 = $B2 30 LAENGE2 = $B5 40 STR1 = $B3 50 STR2 = $B6 55 UMULT1 = $28 56 UMULT2 = $71 57 UMULT = $B357 58 AARRAY = $2F 59 VEKTOR1 = $FB 60 VEKTOR2 = $FD 100 JSR REGSET 101 LDX #0 102 MARKE1 LDA LAENGE1,X 103 STA 700,X 104 INX 105 CPX #6 106 BNE MARKE1 110 JSR HAUPTSCHL 111 LDX #0 112 MARKE2 LDA 700,X 113 STA LAENGE1,X 114 INX 115 CPX #6 116 BNE MARKE2 117 RTS 130 ; 140 HAUPTSCHL JSR HOCHZ 145 JSR HOLLR 150 JSR LRVERGL 160 CMP #0 170 BEQ Z350 180 CMP #2 190 BEQ Z350 195 JSR HOLXY 210 JSR EVINDI 220 Z270 JSR XYVERGL 230 CMP #2 240 BEQ Z330 250 Z280 JSR EXINDI 260 JSR EINSPR 270 CMP #2 280 BEQ Z290 285 CMP #0 286 BEQ Z290 290 JSR HOCHX 300 JMP Z280 310 Z290 JSR EYINDI 320 JSR EINSPR 330 CMP #1 340 BEQ Z300 345 CMP #0 346 BEQ Z300 350 JSR RUNTERY 360 JMP Z290 370 Z300 JSR XYVERGL 380 CMP #2 390 BEQ Z330 400 JSR SWAP 410 JSR HOCHX 420 JSR RUNTERY 430 JMP Z270 435 ; 440 Z330 JSR PUSHLY 460 JSR HAUPTSCHL 470 ; 480 JSR PUSHXR 500 JSR HAUPTSCHL 510 ; 940 Z350 JMP RUNTERZ 1005 ; 1010 ; VERGLEICH STR1 MIT VERGL$ 1011 ;1) STR1>VERGL 2) STR1<VERGL 1015 ; 1020 EINSPR LDY #$FF 1030 SCHL1 INY 1040 CPY LAENGE1 1050 BNE WEITER1 1060 LDA #1 1070 JMP RAUS 1080 WEITER1 CPY LAENGE2 1090 BNE WEITER2 1100 LDA #2 1110 JMP RAUS 1120 WEITER2 LDA (STR1),Y 1130 CMP (STR2),Y 1140 BEQ SCHL1 1150 BCC WEITER3+1 1160 LDA #2 1170 WEITER3 BIT $1A9 ;MASKIERUNG FUER LDA #1 1200 RTS 1210 RAUS LDX LAENGE1 1220 CPX LAENGE2 1230 BNE FERTIG 1240 LDA #0 1250 FERTIG RTS 1260 ; 1270 ; VERGLEICHEN VON X UND Y 1275 ;X<Y LDA #2 X>Y LDA #1 X=Y LDA #0 1280 ; 1290 XYVERGL LDA XREG+1 1300 CMP YREG+1 1310 BNE WEITER4 1320 LDA XREG 1330 CMP YREG 1340 BEQ GLEICH+1 1350 WEITER4 BCS GROESSER+1 1360 LDA #1 1370 GLEICH .BYT $2C,$A9,0 ;BIT $00A9 1380 GROESSER BIT $2A9 1390 RTS 1400 ; 1410 ; VERGLEICHEN VON L UND R 1415 ;L<R LDA #2 L>R LDA #1 L=R LDA #0 1420 ; 1430 LRVERGL LDA LREG+1 1440 CMP RREG+1 1450 BNE WEITER5 1460 LDA LREG 1470 CMP RREG 1480 BEQ GLEICH+1 1490 WEITER5 BCS GROESSER+1 1500 LDA #1 1510 RTS 1985 ; 1990 ; REGISTER HOCH- UNG RUNTERZAEHLEN 1995 ; 2000 HOCHZ CLC 2020 LDA ZREG 2030 ADC #4 2040 STA ZREG 2050 LDA ZREG+1 2060 ADC #0 2070 STA ZREG+1 2090 RTS 2100 RUNTERZ SEC 2120 LDA ZREG 2130 SBC #4 2140 STA ZREG 2150 LDA ZREG+1 2160 SBC #0 2170 STA ZREG+1 2190 RTS 2200 HOCHX CLC 2220 LDA XREG 2230 ADC #1 2240 STA XREG 2250 LDA XREG+1 2260 ADC #0 2270 STA XREG+1 2290 RTS 2300 RUNTERY SEC 2320 LDA YREG 2330 SBC #1 2340 STA YREG 2350 LDA YREG+1 2360 SBC #0 2370 STA YREG+1 2390 RTS 2985 ; 2990 ; DIE MIT X/Y INDIZIERTE VARIABLE 2991 ; WIRD GESUCHT Z.B. ( A$(X) ) 2995 ; 3000 XSUCH LDA XREG 3010 ASL 3015 TAX 3020 LDA XREG+1 3030 JSR PRG1 3040 ADC XREG 3050 TAX 3060 TYA 3070 ADC XREG+1 3080 JMP PRG2 3100 YSUCH LDA YREG 3110 ASL 3115 TAX 3120 LDA YREG+1 3130 JSR PRG1 3131 ADC YREG 3132 TAX 3133 TYA 3134 ADC YREG+1 3135 JMP PRG2 3140 VSUCH LDA VERGL 3150 ASL 3155 TAX 3160 LDA VERGL+1 3170 JSR PRG1 3171 ADC VERGL 3172 TAX 3173 TYA 3174 ADC VERGL+1 3175 JMP PRG2 3200 PRG1 ROL 3210 TAY 3220 TXA 3230 CLC 3240 RTS 3250 PRG2 TAY 3260 CLC 3270 TXA 3280 ADC #7 3281 TAX 3282 TYA 3283 ADC #0 3284 TAY 3285 CLC 3286 TXA 3290 ADC AARRAY 3300 STA VEKTOR1 3310 TYA 3320 ADC AARRAY+1 3330 STA VEKTOR1+1 3340 RTS 3985 ; 3990 ;SWAP - VERTAUSCHEN ZWEIER STRINGS 3995 ; 4000 SWAP JSR XSUCH 4010 LDA VEKTOR1 4020 STA VEKTOR2 4030 LDA VEKTOR1+1 4040 STA VEKTOR2+1 4050 JSR YSUCH 4060 LDY #0 4070 SCHL2 LDA (VEKTOR1),Y 4080 TAX 4090 LDA (VEKTOR2),Y 4100 STA (VEKTOR1),Y 4110 TXA 4120 STA (VEKTOR2),Y 4130 INY 4140 CPY #3 4150 BNE SCHL2 4160 RTS 4985 ; 4990 ; VERGL = (XREG+YREG)/2 4995 ; 5000 RECHNUNG CLC 5010 LDA XREG 5020 ADC YREG 5030 STA VERGL 5040 LDA XREG+1 5050 ADC YREG+1 5060 LSR 5070 STA VERGL+1 5080 ROR VERGL 5090 RTS 5100 ; 5110 ;REGISTER AUF AUSGANGSWERTE SETZEN 5120 ; 5200 REGSET LDA #0 5210 STA XREG 5215 STA XREG+1 5220 LDA #>STACK 5225 STA ZREG 5230 LDA #<STACK 5235 STA ZREG+1 5240 JSR XSUCH 5245 INC XREG 5250 SEC 5260 LDA VEKTOR1 5270 SBC #2 5280 STA VEKTOR1 5290 LDA VEKTOR1+1 5300 SBC #0 5310 STA VEKTOR1+1 5320 LDY #1 5325 SEC 5330 LDA (VEKTOR1),Y 5335 SBC #1 5340 STA YREG 5350 DEY 5360 LDA (VEKTOR1),Y 5365 SBC #0 5370 STA YREG+1 5380 JMP PUSHXY 5985 ; 5990 ;DISCRIPTOREN IN DER ZP EINRICHTEN 5995 ; 6000 EXINDI JSR XSUCH 6010 JMP DISCRIP1 6020 ; 6030 EYINDI JSR YSUCH 6040 ; 6050 DISCRIP1 LDY #0 6060 SCHL3 LDA (VEKTOR1),Y 6070 STA LAENGE1,Y 6080 INY 6090 CPY #3 6100 BNE SCHL3 6110 RTS 6120 ; 6130 EVINDI JSR RECHNUNG 6135 JSR VSUCH 6140 LDY #0 6150 SCHL4 LDA (VEKTOR1),Y 6160 STA LAENGE2,Y 6170 INY 6180 CPY #3 6190 BNE SCHL4 6200 LDA LAENGE2 6205 BEQ KZEICHEN 6210 CMP #21 6220 BCC KLEINER 6230 LDA #20 6240 STA LAENGE2 6250 KLEINER LDY #0 6260 NZEICHEN LDA (STR2),Y 6270 STA VSTR,Y 6280 INY 6290 CPY LAENGE2 6300 BNE NZEICHEN 6310 LDA #>VSTR 6320 STA STR2 6330 LDA #<VSTR 6340 STA STR2+1 6350 KZEICHEN RTS 7000 STCKVEK LDA ZREG 7010 STA VEKTOR2 7020 LDA ZREG+1 7030 STA VEKTOR2+1 7040 RTS 7045 ; 7100 PUSHXR JSR HOLLR 7105 JSR VEKTOR4 7110 LDY #0 7120 SCHL5 LDA XREG,Y 7130 STA (VEKTOR2),Y 7150 INY 7160 CPY #2 7170 BNE SCHL5 7172 SCHL6 LDA RREG-2,Y 7173 STA (VEKTOR2),Y 7174 INY 7175 CPY #4 7176 BNE SCHL6 7177 RTS 7178 ; 7180 PUSHLY JSR HOLLR 7185 JSR VEKTOR4 7190 LDY #0 7200 SCHL7 LDA LREG,Y 7210 STA (VEKTOR2),Y 7230 INY 7240 CPY #2 7250 BNE SCHL7 7261 SCHL8 LDA YREG-2,Y 7262 STA (VEKTOR2),Y 7263 INY 7264 CPY #4 7265 BNE SCHL8 7266 RTS 7270 ; 7280 HOLXY LDY #0 7310 SCHL9 LDA LREG,Y 7320 STA XREG,Y 7330 INY 7340 CPY #4 7350 BNE SCHL9 7360 RTS 7370 ; 7380 HOLLR JSR STCKVEK 7400 LDY #0 7410 SCHL10 LDA (VEKTOR2),Y 7420 STA LREG,Y 7430 INY 7440 CPY #4 7450 BNE SCHL10 7460 RTS 7465 ; 7645 ; 7650 VEKTOR4 JSR STCKVEK 7660 CLC 7670 LDA VEKTOR2 7680 ADC #4 7690 STA VEKTOR2 7700 LDA VEKTOR2+1 7710 ADC #0 7720 STA VEKTOR2+1 7730 RTS 7735 ; 7740 PUSHXY JSR VEKTOR4 7750 LDY #0 7760 SCHL11 LDA XREG,Y 7770 STA (VEKTOR2),Y 7780 INY 7790 CPY #4 7800 BNE SCHL11 7810 RTS 9985 ; 9990 ; REGISTER & EIN SIMULIERTER STACK 9995 ; 10000 ZREG .BYT 0,0 10010 XREG .BYT 0,0 10020 YREG .BYT 0,0 10050 VERGL .BYT 0,0 10060 LREG .BYT 0,0 10070 RREG .BYT 0,0 10080 VSTR .BYT 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ; 20 * 0 10100 STACK .BYT 0 20000 .END READY.
2 ifpeek(2051)<>3thenpoke2051,3:load"quicksort.obj",8,1
5 rem bitte zeile 2 genauso eingeben
10 input "anzahl= 100{left}{left}{left}{left}{left}";a
20 dim a$(a)
23 rem
25 rem jedes element mit 3 zeichen
28 rem
30 for i = 1 to a
35 : for j = 0 to 2
40 : a$(i) = a$(i)+chr$(rnd(1)*26+65)
50 : next j
55 next i
56 rem
57 rem elememte ausgeben
58 rem
60 for i = 1 to a
63 : print a$(i);" ";
65 next i
66 print
67 rem
68 rem elemente sortieren
69 rem
70 ti$ = "000000"
74 sys 52000
76 t = ti
77 rem
78 rem elemente ausgeben
79 rem
80 for i= 1 to a
85 : print a$(i);" ";
90 next i
95 print t/60
