Sortieren mit dem Computer (Teil 4)
Quicksort verdient seinen Namen zu Recht. Aber er kann auch zu einem ausgesprochenen Langweiler werden. Sogar Bubblesort kann schneller sein als alle anderen Sortierroutinen. Woran das liegt, erfahren Sie im folgenden Artikel.
Der Quicksort-Algorithmus wurde bereits 1962 von R. Hoare entwickelt und ist trotzdem bis heute die schnellste Methode zum Sortieren großer, zufallsbesetzter Felder geblieben. Der Deutlichkeit halber betone ich noch einmal zufallsbesetzt, denn nur bei dieser Art der Verteilung der Feldelemente kann Quicksort wirklich effektiv arbeiten. Haben wir ein Array, das zum Beispiel absteigend sortiert ist (9, 8, 7,…, 1) und sollen hier nur wenige Elemente neu einsortiert werden, so wird Quicksort im wahrsten Sinne des Wortes zum »Slowsort« und benötigt eine ewige Zeit zur Bearbeitung des Feldes.
Andererseits lohnt sich der Einsatz von Quicksort auch dann nicht, wenn es darum geht, beispielsweise eine Kartei zu führen, bei der laufend neue Elemente in ein schon vorsortiertes Feld eingefügt werden sollen (zum Beispiel der Buchstabe D in das Feld A, B, C, F, H, M, N, O,…).
Hier eignet sich unser (normalerweise langsamster) Bubblesort-2-Algorithmus sehr gut; in diesem Fall findet nämlich nur ein einziger Durchlauf statt, bevor der Algorithmus beendet wird (wie Sie wissen, verwendet Bubblesort 2 eine zusätzliche Variable, die anzeigt, ob noch weitere Sortierdurchläufe notwendig sind).
Bei der Effektivität unserer Sortierprogramme sollen uns diese Spezialanwendungen jedoch nicht weiter interessieren. Hier geht es nur um das Problem, ein völlig »durcheinandergeratenes« Feld wieder in Ordnung zu bringen, und das bitte möglichst schnell.
Wie funktioniert Quicksort?
So wollen wir uns nun einmal den Quicksort-Algorithmus etwas genauer betrachten. Er ist nicht im mindesten mit den bisherigen Methoden zu vergleichen, und wunderbarerweise zählt er trotz seiner Leistungsfähigkeit zu den etwas leichter verständlichen Algorithmen.
Das Prinzip von Quicksort ist folgendes:
Zuallererst wird aus dem gesamten Variablenfeld ein (beliebiges) Element herausgegriffen und »beiseite gelegt«. Dieses Element dient nun als Vergleichswert für das gesamte übrige Array. Jetzt werden alle Elemente, die kleiner als das Vergleichselement sind, links (also auf niedrigere Positionen) und alle Elemente, die größer sind, rechts (also auf höhere Positionen) vom Vergleichselement abgespeichert. Wir erhalten so ein Variablenfeld, bei dem alle kleineren Elemente oberhalb und alle größeren Elemente unterhalb des Vergleichselements stehen. Bild 1 zeigt noch einmal genau, was gemeint ist.
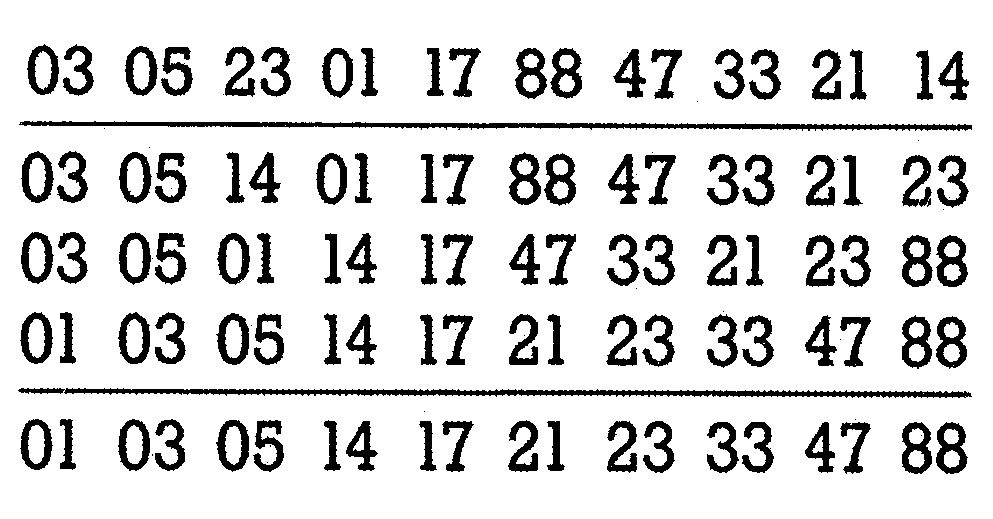
Nachdem diese »Gesamtsortierung« vollzogen wurde, haben wir ein schon sehr grob sortiertes Feld vorliegen. Nun teilen wir die beiden neuen Teilfelder (oberhalb und unterhalb des Vergleichselements) wiederum durch jeweils ein neues Vergleichselement auf, wobei diese beiden Teilfelder auf die oben beschriebene Art erneut sortiert werden. Als Ergebnis haben wir dann vier teilsortierte Feldabschnitte vorliegen, die wiederum, jedes für sich, geteilt und sortiert werden.
Setzen wir diese Teilungen immer weiter fort, so werden wir irgendwann einmal die Teilfeldlänge 1 erreichen, womit unser Gesamtfeld fertig sortiert wäre.
Wie Sie sicherlich bemerken, ist die Effektivität dieses Algorithmus natürlich stark von der Wahl des jeweiligen Vergleichselements abhängig. Optimal wäre jedesmal ein Vergleichselement, das etwa das Mittel der zugehörigen Teilliste ausmacht und diese so in zwei gleich große Abschnitte trennt.
Die Suche nach einem solchen optimalen Vergleichselement würde sich jedoch so aufwendig gestalten, daß die Geschwindigkeit von Quicksort stark darunter leiden müßte. Aus diesem Grund geht man bei der Wahl des betreffenden Elements einen anderen Weg. Es wird einfach jedesmal das Element gewählt, das genau in der Mitte der Teilliste steht. Auf diese Weise erhält man bei zufallsbesetzten Feldern zwar auch sehr ungünstige Werte; dieser Mangel wird jedoch durch eine ebensogroße Zahl von extrem günstigen Werten ausgeglichen.
Im Geschwindigkeitstest zeigt dieser Quicksort-Algorithmus dann auch seine verblüffenden Eigenschaften.
Bevor wir jedoch auf einen Vergleich sämtlicher bisher besprochener Sortiermethoden eingehen, noch etwas zur Programmierung von Quicksort.
Was ist rekursives Programmieren?
Während des Programmablaufs kommt ein Unterprogramm immer wieder in der gleichen Form vor und zwar das Sortieren eines Teilfeldes anhand des Vergleichselements. Dieses Unterprogramm stellt nun auch die neuen Teillisten fest und müßte bei einem sofortigen Rücksprung mit »RETURN« sämtliche neuen Parameter zwischenspeichern, um dann erneut aufgerufen zu werden …
Diese umständliche Programmiertechnik, die für einen linearen Programmablauf sorgt, wurde bei Quicksort nicht verwendet. Hier werden vielmehr die neu festgestellten Teillisten sofort wieder bearbeitet, um danach ebenfalls wieder die nächsten Teillisten herzustellen.
Wie funktioniert nun eine solche Programmiertechnik?
Man geht davon aus, daß der eigentliche Sortier- und Teilalgorithmus in einer Unterroutine untergebracht ist, wobei diese mit GOSUB aufgerufen wird. Wurde nun die erste Teilung des Variablenfeldes durchgeführt, so werden sofort die Werte für die nächste Halbierung dieser beiden Teilfelder bereitgestellt. Danach ruft sich die Unterroutine sofort wieder selbst auf, um auch die neue Sortierung und Teilung ablaufen zu lassen. Dabei entstehen wieder zwei neue Teilfelder, die wiederum sofort bearbeitet werden, etc. …
Bild 2 zeigt anschaulich, was gemeint ist.
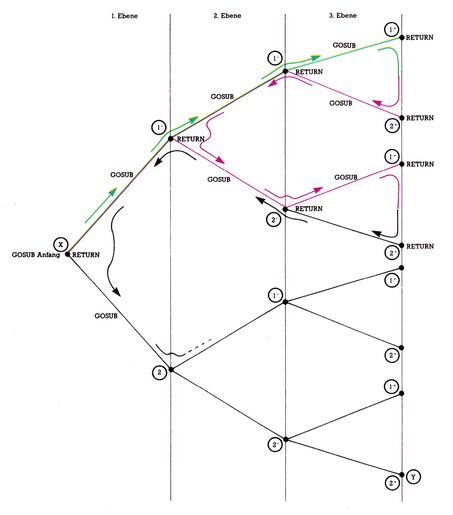
Erklärung zu Bild 2:
Das rekursive Unterprogramm arbeitet immer innerhalb eines Aufrufes zwei Teilfelder ab, indem es zwischen beiden die Elemente vertauscht (Sortierung anhand des Vergleichselements).
Die rekursive Technik funktioniert nun wie ein Baum, bei dem nacheinander alle Äste abgefahren werden. Zuerst wird das Gesamtfeld in zwei Teilfelder (entsprechend des Vergleichselements) aufsortiert (1. Ebene). Von diesen zwei Teilfeldern wird nun zuerst das erste Teilfeld wiederum aufgeteilt (grüner Pfeil X → 1). Da noch nicht Länge 1 erreicht wurde, wird das neue Teilfeld wiederum aufgeteilt (grüner Pfeil 1' → 1''). Jetzt haben die Teilfelder die Länge 1 und sind vollständig sortiert, weshalb nun auf eine höhere Ebene (RETURN bei 1'' und 2'') zurückgekehrt wird (roter Pfeil 2'' → 1' → 1).
Jetzt wird (wiederum mit GOSUB) das zweite Teilfeld der 2. Ebene (2') ebenfalls vollständig sortiert....
Diese Vorgänge wiederholen sich, bis beim Punkt Y mit drei RETURNs wieder ganz zurückgesprungen wird, da das Unterprogramm auf 1. Ebene vollständig abgearbeitet wurde.
Eine solche Programmiertechnik, bei der sich Programmteile selbst aufrufen, nennt man rekursiv!
Nun, könnten Sie jetzt einwenden, dieses Programm verschachtelt sich doch immer weiter, ohne daß ein Ende abzusehen ist. Wie findet der Computer denn aus diesem »Irrgarten« wieder heraus?
Die Sache ist relativ einfach. Irgendwann wird der Computer bei der Teillistenlänge 1 angekommen sein. Hat er das festgestellt, so erfolgt kein weiterer Selbstaufruf mehr, sondern es wird ein »RETURN« durchgeführt. Jetzt ist aber unser Unterprogramm so ausgelegt, daß es jeweils alle Teillisten der gleichen Länge nacheinander bearbeitet. Erfolgt also das erste RETURN, so bearbeitet der Computer die zweite Teilliste der Länge 2, bis er auch hier wieder teilt und bei 1 ankommt…
Dieses Bearbeiten der zwei letzten Teillisten setzt sich so lange fort, bis der Computer bei der letzten Teilliste dieser Ebene angekommen ist. Hier erfolgt wiederum ein RETURN, so daß nun auf die drittletzte Ebene mit der Größe 4 zurückgesprungen wird. Auch dort werden sämtliche Elemente bearbeitet, bis wir irgendwann wieder bei einer Teilliste der Länge A (gesamtes Feld) angekommen sind, worauf der Quicksortalgorithmus verlassen wird.
Dieses Prinzip ist nicht so ohne weiteres verständlich. Am besten sehen Sie sich noch einmal Bild 2 an; dort ist der ganze rekursive Algorithmus grafisch dargestellt.
An der Geschwindigkeit von Quicksort wird deutlich, wie effektiv rekursive Programmiertechnik sein kann.
Probleme der Rekursion in Basic
Bei unserem Quicksort in Basic stellt sich jedoch noch ein zusätzliches Problem: Basic ist keine strukturierte Sprache!
Was das bedeutet, sei am Beispiel von Pascal kurz erläutert.
Bei einer strukturierten Sprache werden Unterprogramme als eigene Einheiten mit eigenen Variablen betrachtet. Es kann also vorkommen, daß eine Unterroutine die gleichen Variablen wie das übergeordnete Programm enthält, wobei diesen jedoch andere Werte zugeordnet sind.
Hat also beispielsweise das Hauptprogramm in Pascal eine Variable X mit dem Wert 3 belegt und springt nun ein Unterprogramm an, in dem diese Variable ebenfalls verwendet wird, so wird der Inhalt von X auf einen Software-Stack gerettet und erst anschließend das Unterprogramm aufgerufen. Bei der Rückkehr aus dieser Unterroutine holt der Computer den Wert von X wieder vom Stack und übergibt ihn dem Hauptprogramm.
Bei einer rekursiven Programmiertechnik bleiben also alle Parameter, die von einer Routine erarbeitet wurden, erhalten und können später, gemäß der Reihenfolge, weiter verwendet werden.
Nicht so in Basic!
Hier gibt es nur jeweils eine Variable gleichen Namens, deren Wert sowohl vom Hauptprogramm als auch von Unterroutinen gleichermaßen beeinflußt werden kann. Haben Sie also die Variable X mit dem Wert 3, so erfolgt bei einem Unterprogramm, in dem es heißt: X = 5, ein Verlust der 3, der auch bei der Rückkehr ins Hauptprogramm nicht aufgehoben wird.
Aus diesem Grund können Sie im Basic-Quicksort noch ein weiteres Variablenfeld erkennen, in dem die wichtigen Parameter der Teilfelder abgespeichert werden, damit sie bei der Rückkehr von einer Ebene auf eine höhere wieder zur Verfügung stehen.
Wenn Sie das Prinzip der rekursiven Programmiertechnik noch nicht ganz verstanden haben, sollten Sie nicht die Mühe scheuen, noch einmal von vorne mit dem Lesen dieses Artikels zu beginnen. Diese Programmiermethode eignet sich nämlich zu allen algorithmischen Lösungen von Problemen mit ähnlicher Struktur, und Sie werden anhand von Quicksort erkennen können, wie effektiv und leistungsstark ein solches Programm wird.
Wie leistungsstark unsere sämtlichen Sortierprogramme sind, das soll im folgenden dargestellt werden, wobei Sie auch für Quicksort wieder einen Programmablaufplan vorfinden, der das Umschreiben auf andere Programmiersprachen erleichtern soll (Bild 3).
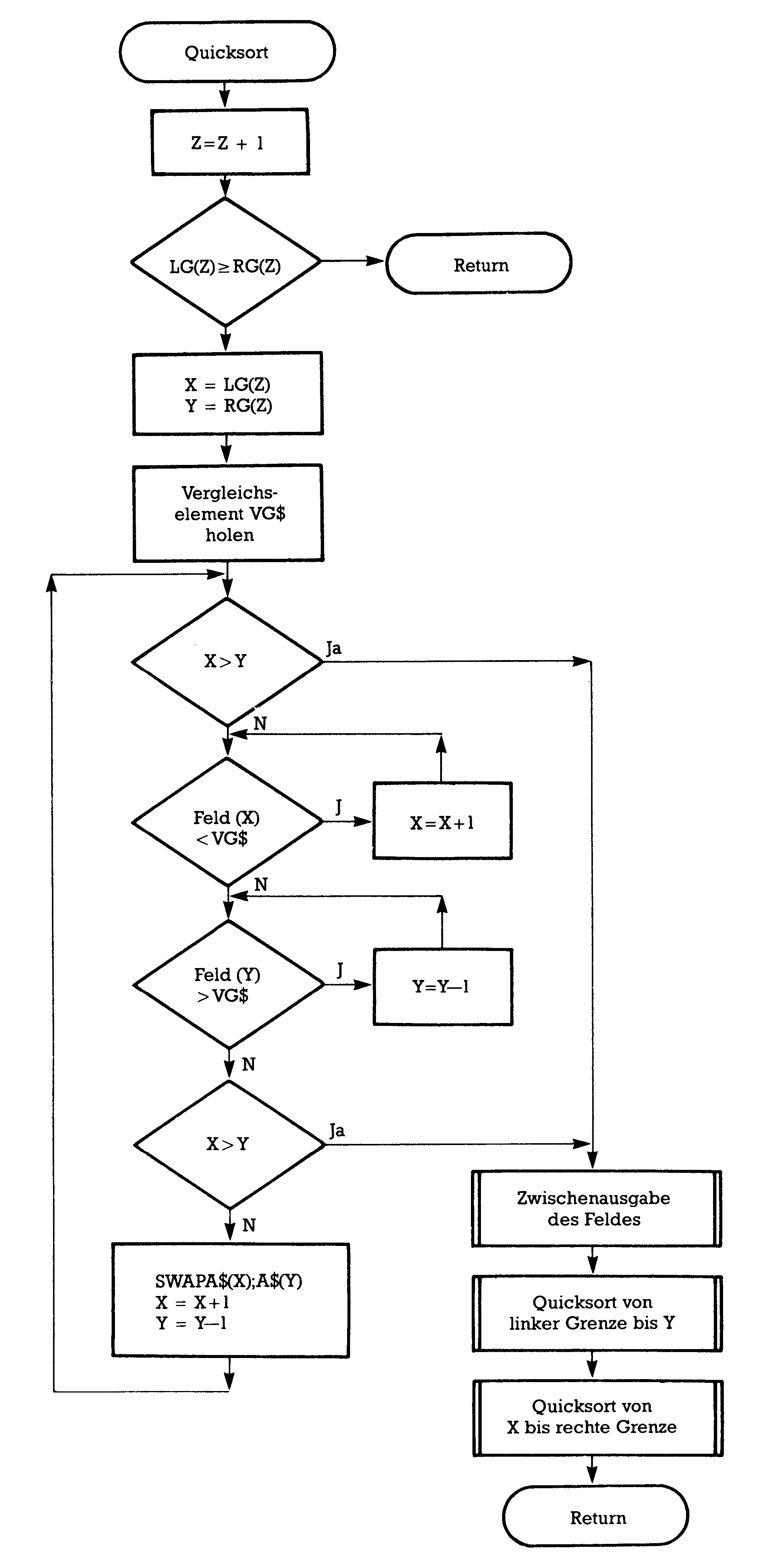
Nun aber zu unserem Vergleichstest.
Für diesen Test habe ich sämtliche Sortierprogramme soweit optimiert, indem ich alle REMs und alle zusätzlichen Leerzeichen entfernt habe. Außerdem wurde die dauernde Zwischenausgabe der Daten auf Bildschirm oder Drucker weggelassen, so daß sich die Zeitmessung jetzt nur auf den reinen Algorithmus bezieht.
Sortieralgorithmen im Vergleich
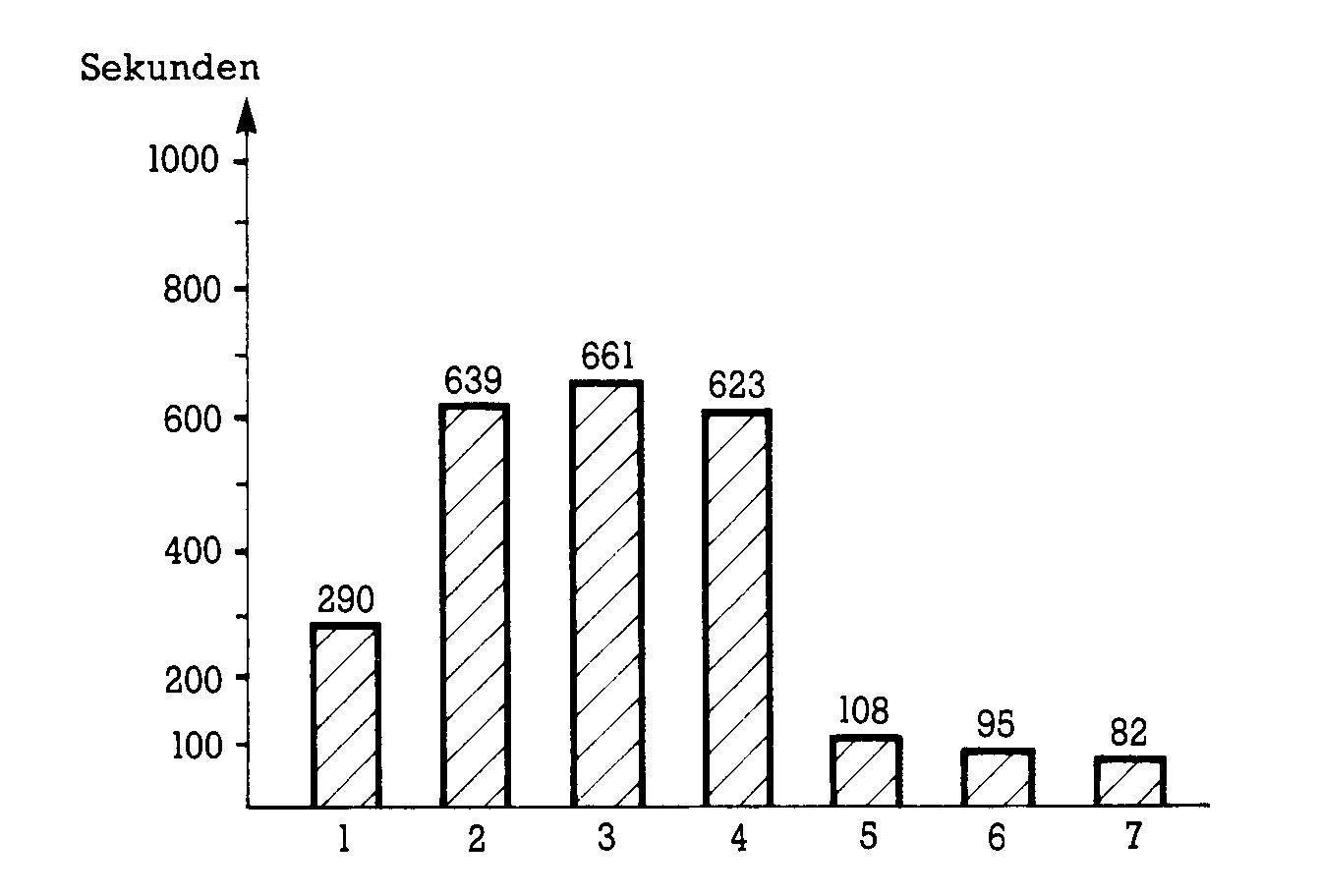
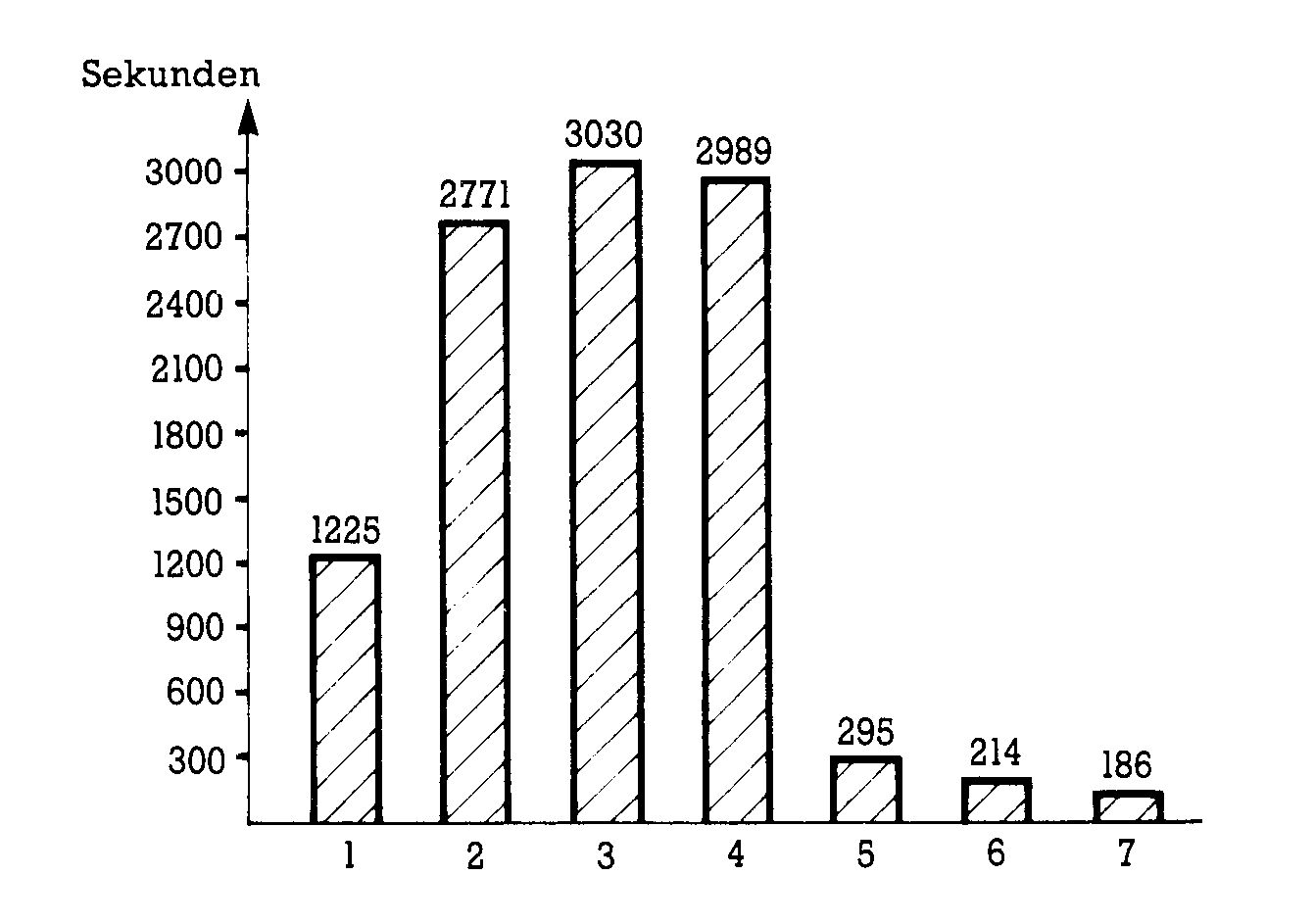
Getestet wurde bei allen Kandidaten ein zufallsbesetztes Feld von jeweils 100, 250 und 500 Elementen. Die Ergebnisse dieses Tests sind in Bild 4 dargestellt. Wie Sie sehen, schneidet Quicksort mit Abstand am besten ab; dicht gefolgt von Heapsort und etwas weiter von Shellsort. Diese drei Sortiermethoden eignen sich also für den praktischen Einsatz bei zufallsbesetzten Feldern, wobei im Vergleich zu den »niederen« Algorithmen sehr große Zeitvorteile zu verzeichnen sind. Bei 500 Elementen ist beispielsweise Quicksort über 16mal so schnell, wie unser (verbesserter) Bubblesort-2-Algorithmus.
| Sortierprogramm | Anzahl der Elemente | ||
| 100 | 250 | 500 | |
| 1) Straight Insertion: | 45 s | 290 s | 1225 s |
| 2) Bubblesort: | 99 s | 639 s | 2771 s |
| 3) Bubblesort 2: | 99 s | 661 s | 3030 s |
| 4) Straight Select: | 100 s | 623 s | 2989 s |
| 5) Shellsort: | 37 s | 108 s | 295 s |
| 6) Heapsort: | 31 s | 95 s | 214 s |
| 7) Quicksort: | 30 s | 82 s | 186 s |
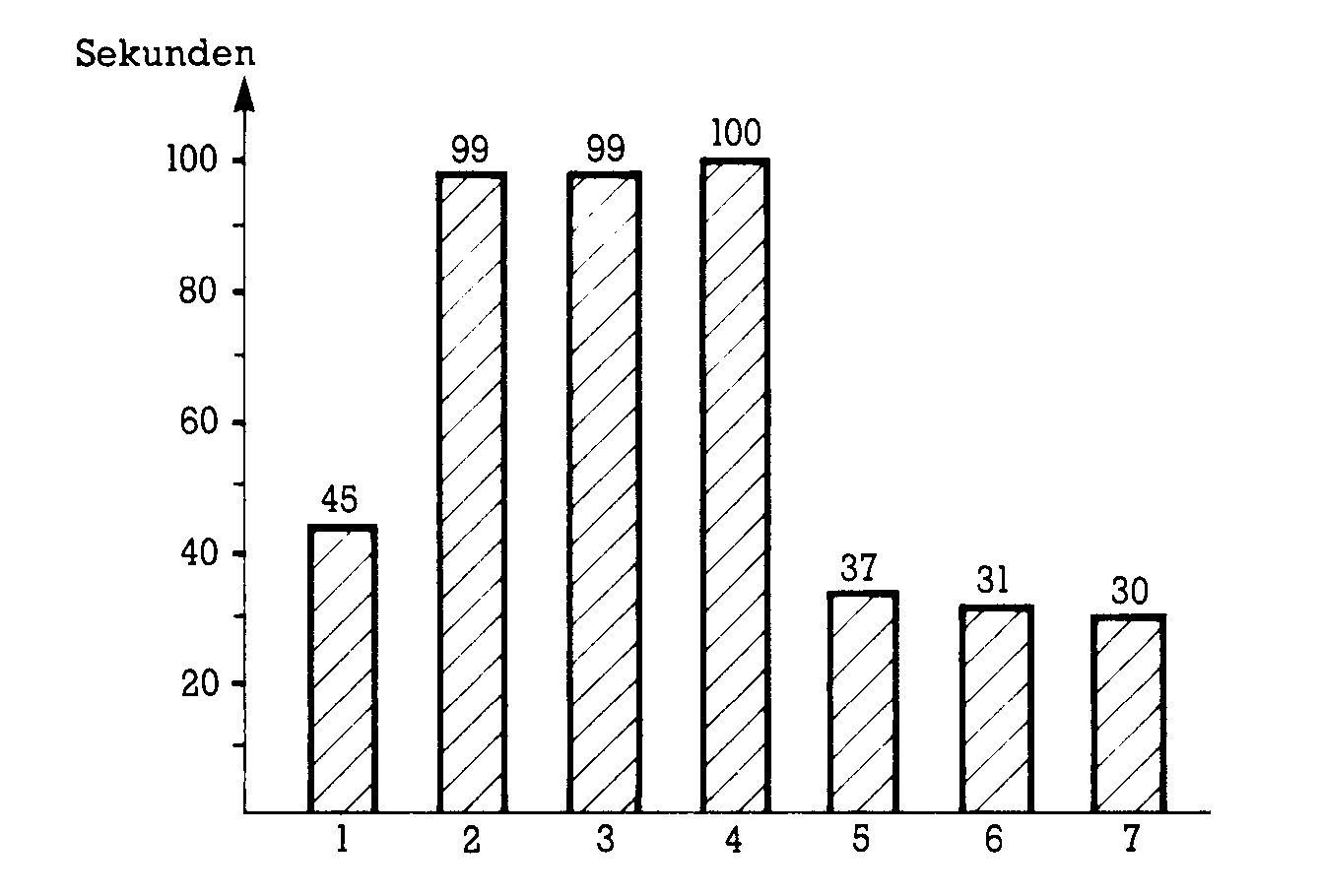
Wie Sie sicherlich ahnen, hat diese schlechte Zeit, die sogar unser »normales« Bubblesort unterbietet, etwas mit der zusätzlichen Abfrage auf Vertauschungen zu tun.
Bei zufallsbesetzten Feldern ist Bubblesort 2 nicht akzeptabel!
Haben wir jedoch ein schon aufsteigend sortiertes Feld vorliegen, bei dem nur einige neue Elemente eingefügt werden sollen, so wird Bubblesort 2 fast unschlagbar, da hier die zusätzliche Abfrage für ein schnelles Ende, ohne zusätzliche, unnötige Arbeit, sorgt.
Bei unseren kleinen Variablenfeldern können also mit den höheren Sortierprogrammen ohne weiteres gute Zeiten erreicht werden.
Kritisch wird die ganze Angelegenheit jedoch, wenn Sie mit großen Feldern arbeiten, wobei unter Umständen noch ein riesiges Programm im Speicher steht.
Hier bekommt man es dann sehr schnell und auf höchst unangenehme Weise mit der »Müllabfuhr im Computer«, der Garbage Collection, zu tun (64'er, Ausgabe 1/1985, Seite 122).
Diese Tatsache ist jedoch nicht weiter verwunderlich, wenn man bedenkt, daß wir bei zufallsbesetzten Feldern beinahe das gesamte Array neu definieren und dabei entsprechend viel »Müll« erzeugen.
Sortieren ohne Müll
Haben Sie vielleicht schon einmal an eine andere Methode der Sortierung von Arrays gedacht? Es gibt nämlich noch eine weitere Möglichkeit, bei der man ohne viele Stringverschiebungen auskommt. Diese Möglichkeit der Sortierung und das Problem der Garbage Collection soll uns das nächstemal interessieren, wo wir uns dann einmal mit dem Sortieren der Indizes der Feldvariablen befassen. Außerdem können Sie sich schon einmal Gedanken zum Thema »Sortieren mehrdimensionaler Felder« machen. Das ist nämlich nicht annähernd so leicht, wie es vielleicht aussehen mag und erfordert eine ganze Menge Schweiß.
Für heute wollen wir es aber nun genug sein lassen. Experimentieren Sie doch ein wenig mit Quicksort, und lernen Sie diesen Algorithmus genauer kennen. Ich bin davon überzeugt, daß sich Ihnen früher oder später ein Problem stellt, bei dem Sie auf einen guten und schnellen Sortieralgorithmus angewiesen sein werden und den Sie nun Dank R. Hoare auch besitzen.
(Karsten Schramm/gk)10000 rem sortieren durch zerlegen 10010 rem 10020 rem quicksort 10030 rem 10040 rem lg = linke grenze 10050 rem rg = rechte grenze 10060 rem vg$ = vergleichselement 10070 rem 10080 rem eingang des hauptmoduls 10090 rem 10100 dimlg(100),rg(100):z=0:lg(1)=1:rg(1)=a 10110 gosub10200: rem quicksort 10120 goto50000:rem ende 10200 rem eingang der rekursivschleife 10210 z=z+1:iflg(z)>=rg(z)then10350 10220 x=lg(z):y=rg(z) 10225 rem vergleichselement holen 10230 vg$=a$(int((x+y)/2)) 10240 ifx>ythen10320 10250 ifa$(x)<vg$thenx=x+1:goto10250 10260 ifa$(y)>vg$theny=y-1:goto10260 10270 ifx>ythen10320 10280 s$=a$(x):a$(x)=a$(y):a$(y)=s$ 10290 x=x+1:y=y-1 10300 goto10240 10310 rem 10320 gosub3000 10330 rg(z+1)=y:lg(z+1)=lg(z):gosub 10200 10340 lg(z+1)=x:rg(z+1)=rg(z):gosub 10200 10350 z=z-1:return 10360 rem
10040 forx=2toa 10050 ifa$(x)>=a$(x-1)then 10120 10070 x$=a$(x):fory=x-1to1step-1 10080 a$(y+1)=a$(y) 10090 ifx$<=a$(y-1)then 10110 10100 a$(y)=x$:goto10120 10110 nexty 10120 nextx
10040 forx=a-1to1step-1 10050 fory=1tox 10060 ifa$(y)<=a$(y+1)then10080 10070 s$=a$(y):a$(y)=a$(y+1):a$(y+1)=s$ 10080 nexty 10090 nextx
10040 forx=ato2step-1:x$="" 10050 fory=1tox 10060 ifa$(y)>x$thenx$=a$(y):z=y 10070 nexty 10080 s$=a$(x):a$(x)=a$(z):a$(z)=s$ 10090 nextx
10040 g=a-1:forx=a-1to1step-1 10050 f=0:fory=1tog 10060 ifa$(y)<=a$(y+1)then10080 10070 f=y:s$=a$(y):a$(y)=a$(y+1):a$(y+1)=s$ 10080 nexty 10090 g=f:iff=0then50000 10100 nextx
10035 dim aa$(a) 10040 s=int(a/2) 10050 forx=1tos 10060 fory=1toint(a/s) 10070 aa$(y)=a$((y-1)*s+x) 10080 nexty 10090 aa=y-1:gosub20000 10100 fory=1toint(a/s) 10110 a$((y-1)*s+x)=aa$(y) 10120 nexty 10130 nextx 10140 s=int(s/2) 10160 ifsgoto10050 10180 goto50000 20000 forxx=2toaa 20010 ifaa$(xx)>=aa$(xx-1) then 20080 20030 xx$=aa$(xx):foryy=xx-1to1step-1 20040 aa$(yy+1)=aa$(yy) 20050 ifxx$<=aa$(yy-1)then 20070 20060 aa$(yy)=xx$:goto20080 20070 nextyy 20080 nextxx 20090 return
10040 lg=int(a/2)+1:rg=a 10050 ifrg<=1then50000 10060 iflg<=1then10110 10080 lg=lg-1 10090 i=lg:goto10140 10110 s$=a$(1):a$(1)=a$(rg):a$(rg)=s$ 10120 rg=rg-1 10130 i=1 10140 x$=a$(i) 10150 p=0 10160 if2*i<=rgandp=0then10210 10170 a$(i)=x$ 10180 goto10050 10210 j=2*i 10220 ifj<rgthenifa$(j)<a$(j+1)thenj=j+1 10230 ifx$>=a$(j)then10260 10240 a$(i)=a$(j) 10250 i=j:goto10160 10260 p=1:goto10160
10100 dimlg(100),rg(100):z=0:lg(1)=1:rg(1)=a 10110 gosub10210 10120 goto50000 10210 z=z+1:iflg(z)>=rg(z)then10350 10220 x=lg(z):y=rg(z) 10230 vg$=a$(int((x+y)/2)) 10240 ifx>ythen10330 10250 ifa$(x)<vg$thenx=x+1:goto10250 10260 ifa$(y)>vg$theny=y-1:goto10260 10270 ifx>ythen10330 10280 s$=a$(x):a$(x)=a$(y):a$(y)=s$ 10290 x=x+1:y=y-1:goto10240 10330 rg(z+1)=y:lg(z+1)=lg(z):gosub 10210 10340 lg(z+1)=x:rg(z+1)=rg(z):gosub 10210 10350 z=z-1:return
