Effektives Programmieren (6): Sortieren mit dem Computer — (Teil 3)

Nachdem wir in den letzten beiden Folgen mehrere einfache Sortieralgorithmen besprochen haben, wollen wir uns diesmal nur mit einem einzigen Algorithmus auseinandersetzen, dem Heapsort. Heapsort ist mit Sicherheit die komplizierteste der bekannten Sortiermethoden und verdient deshalb unsere ganze Aufmerksamkeit, zumal sie dazu noch eine der schnellsten ist.

Zuerst einmal zum Ausdruck »heap«. Ein Heap (engl.: Haufen, Menge) bezeichnet ein Variablenfeld, das auf eine ganz bestimmte Art sortiert wurde und damit einige wichtige Eigenschaften erfüllt, auf die wir später noch zu sprechen kommen werden.

Grundlagen

Beschäftigen wir uns zunächst einmal mit dem Grundgedanken des Heapsort. Unsere bisherigen Sortierprogramme waren alle relativ langsam. In den beschriebenen Formeln konnte man das durch den Faktor A² erkennen, der besagt, daß die Sortierzeit mit dem Quadrat der Feldgröße steigt. Die Ursache für diese ungünstigen Zeiten war die oft unnötige Anzahl von Durchläufen, obwohl gewisse Voraussetzungen schon gegeben waren. Anders ausgedrückt haben unsere bisherigen Programme bei ihren Durchläufen nie alle Informationen genutzt, die ihnen zur Verfügung standen. Heapsort hat an dieser Stelle etwas geändert. Der Sortieralgorithmus verarbeitet bei jedem Durchlauf mehrere Informationseinheiten, die dann ein systematischeres Vorgehen erlauben.

Was ist ein »Baum«?

Um Heapsort zu verstehen, müssen wir uns jetzt ersteinmal mit dem mathematischen Begriff des »Baums« beschäftigen. Ein mathematischer Baum ist eine Anordnung von Elementen einer Menge. Ein Beispiel für einen Baum sehen Sie in Bild 1. Jetzt stellt sich natürlich die Frage, wie wir einen solchen Baum in unsere Feldstruktur überführen können, denn immerhin ist ein Baum zweidimensional, wir arbeiten jedoch nur mit eindimensionalen Feldern. Sehen Sie sich dazu einmal Bild 2 an. Es zeigt den Baum aus Bild 3 in eindimensionaler Darstellung als Feld. Wie Sie sehen können, ist die Aufstellung streng hierarchisch und berechnet sich wie folgt: Wir nehmen ein Element an einer Position I. Handelt es sich bei unserer Menge aus Elementen um einen Heap (Variablenfeld), so muß der Wert an der Stelle INT (1/2) größer oder gleich des Wertes an der Stelle I sein. Mathematisch beschrieben sieht die Sache folgendermaßen aus (wobei A$(I) ein Feldelement ist):

A$(INT(I/2)) >= A$(I), für 2 <= I <= A (A ist die Gesamtanzahl der Elemente des Feldes).

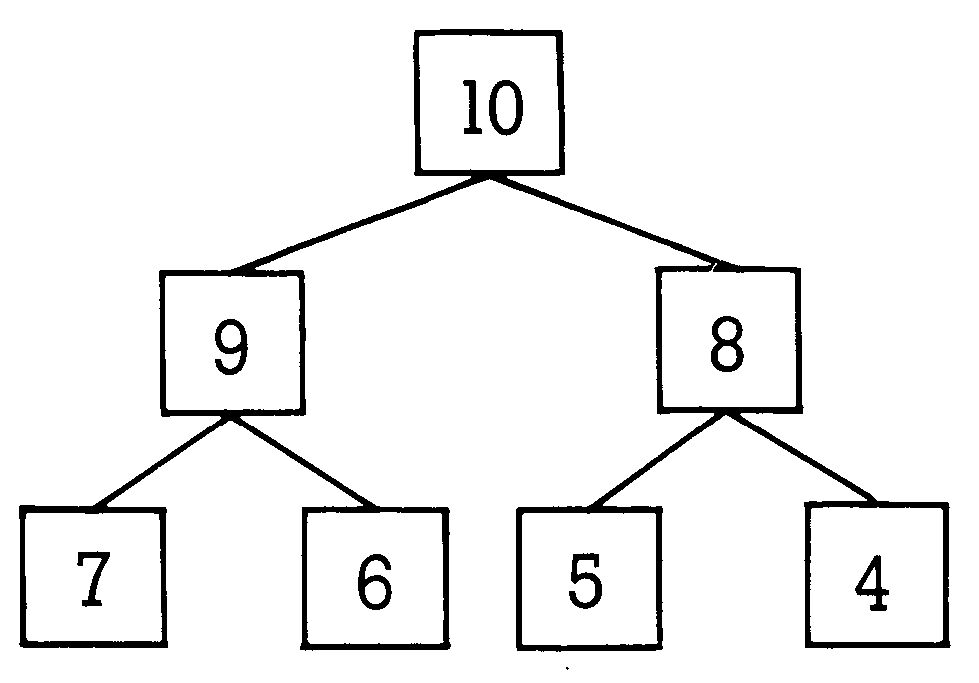
Anschaulich können wir sagen, daß das Element A$ (INT(I/2)) immer der nächsthöhere »Knoten« des Baumes über den Elementen A$(I) und A$(I + 1) ist.

Welchen Sinn hat die Baumstruktur?

Sie werden sich jetzt sicherlich fragen, was denn der Vorteil dieser recht komplizierten Baumstruktur ist. Nun, wir sind jetzt in der Lage, in einem Feld, welches einer Baumstruktur entspricht, ganz einfach nach einem Element die Position der nächstgrößeren, beziehungsweise die Position der nächstkleineren Elemente festzustellen und haben damit schon einmal eine Vorsortierung erreicht. Wie Sie vielleicht schon gemerkt haben, lassen sich die Positionen durch die oben genannte Formel ganz leicht aus der Position des Ausgangselements berechnen. Wenn Sie sich noch einmal die Bedingung für einen Baum betrachten, so werden Sie erkennen, daß auch Sonderfälle auftreten können. So kann ein Feld beispielsweise keinen vollständigen Baum darstellen, sondern nur ab einer gewissen Stelle eine Sortierung aufweisen, die der obigen Formel entspricht (Bild 3 zeigt ein Beispiel für eine solche Sortierung). Diese Form der Sortierung bezeichnet man als Heap. Ein Heap ist also nicht vollständig durchsortiert; er zeigt jedoch eine Eigenschaft, die für unser Sortieren von entscheidender Bedeutung ist: das Maximum des Feldes steht jeweils an der Spitze, also auf Position 1.

Nehmen wir jetzt einmal an, Sie entfernen das Element an der Spitze des Heap und setzen den Rest des Feldes wieder zusammen. Der Arrayrest besteht jetzt aus A-1 Elementen, unter denen sich nun das zweitgrößte befindet. Jetzt stellen Sie diese A-1 Elemente wieder so zusammen, daß ein Heap entsteht…

Wie die Reihe weitergeht, können Sie sich jetzt bestimmt denken. Wir nehmen wiederum das erste Element weg und haben somit das insgesamt zweitgrößte Element aussortiert. Diese Schritte wiederholen sich so lange, bis nur noch ein Element, das kleinste, im Heap übrigbleibt. Durch die relativ geordnete Struktur des Variablenfeldes während der Arbeit sind keine langen Suchzeiten erforderlich. Das verkürzt die Sortierdauer erheblich.

Die Formel zeigt die Berechnung der mittleren Anzahl der Bewegungen bei einem Sortiervorgang, wobei A die Anzahl der Elemente des Feldes angibt:

mittbew = ungefähr 1/2*A*ld(A)

Heapsort ist schneller, als die bisherigen Sortiermethoden

An dieser Stelle zeigt sich bereits der deutliche Unterschied von Heapsort zu den vorher besprochenen Sortiermethoden. Während diese immer den Faktor A² in ihren Formeln hatten, steigt die Zahl der Bewegungen bei Heapsort im Mittel nur um den Faktor ld (A), wobei ld den Logarithmus zur Basis 2 darstellt. Der Logarithmus ld kann durch den natürlichen Logarithmus (ln) auf die folgende Art dargestellt werden:

ld(A) = ln(A)/ln(2).

An dieser Stelle gleich einmal eine Bemerkung zum Logarithmus: Auf dem C 64 und auf dem VC 20 existiert jeweils nur der natürliche Logarithmus (ln). Im Basic-Dialekt dieser Computer wird jedoch eine unübliche Abkürzung für diesen Logarithmus verwendet. Eine Berechnung erfolgt hier mit dem Befehl LOG, der eigentlich für den Logarithmus der Basis 10 (Zehnerlogarithmus) steht.

Jetzt aber wieder zurück zu Heapsort. In Bild 4 können Sie erkennen, was vorher besprochen wurde. Unser Beispiel-Heap aus Bild 3 wird sortiert, wobei jeweils das erste Element aussortiert und dann der Rest des Arrays wieder zusammengesetzt wird.

Das Programm zu Heapsort ist in Listing 1 dargestellt und benötigt zu seiner Ausführung die beiden anderen Programmteile, die als Listing 1 und 2 in der 64'er, Ausgabe 4/1985 auf Seite 149 abgedruckt wurden. Um die Abfragepunkte bei Heapsort deutlich darzustellen, wurde in Listing 1 auf FOR-NEXT-Schleifen verzichtet, was allerdings zu Lasten der Geschwindigkeit geht. Wenn wir in der nächsten Ausgabe Quicksort besprechen, werden wir unter anderem auch auf Geschwindigkeitsfaktoren (Garbage-Collection, Vergleiche, Indizierung) eingehen. Außerdem werden wir einen Zeitvergleich über alle bisher besprochenen Routinen durchführen, zu dessen Zweck die Programme natürlich optimiert werden. Bild 5 zeigt einen Ausdruck von Heapsort während der Arbeit. In Bild 6 sehen Sie, wie schon in den vorherigen Folgen, einen Programmablaufplan, anhand dessen es keine großen Probleme bereiten sollte, Heapsort für eigene Anwendungen oder auf andere Programmiersprachen umzuschreiben.

Hiermit wollen wir es für heute aber auch schon bewenden lassen. Heapsort dürfte Sie sicherlich noch einige Zeit beschäftigen, da diese Methode nicht ganz leicht zu durchschauen ist. In der nächsten Folge werden wir uns ausführlich mit dem Quicksort beschäftigen, dem wohl schnellsten Sortieralgorithmus.

10000 rem sortieren mit baeumen
10010 rem
10020 rem heapsort
10030 rem
10040 lg=int(a/2)+1:rg=a
10050 if rg<=1 then 10190
10060 if lg<=1 then 10100
10070 rem aufbau des haufens
10080 lg=lg-1
10090 i=lg:goto 10140
10100 rem wegnehmen des maximums
10110 s$=a$(1)=a$(1)=a$(rg):a$(rg)=s$
10120 rg=rg-1
10130 i=1
10140 x$=a$(i)
10150 p=0:rem flag fuer nicht gefunden
10160 if 2*i<=rg and p=0 then 10200
10170 a$(i)=x$
10180 gosub 3000: goto 10050
10190 goto 10300: rem ende
10200 rem feldvariable a$(i) einordnen
10210 j=2*i
10220 if j<rg then if a$(j)<a$(j+1)then j=j+1
10230 if x$>=a$(j) then 10260
10240 a$(i)=a$(j)
10250 i=j:goto 10160
10260 p=1:rem flag fuer platz gefunden
10270 goto 10160
10280 :
10290 :
10300 rem ende

 10000 REM SORTIEREN MIT BAEUMEN 
 10010 REM 
 10020 REM HEAPSORT 
 10030 REM 
 10040 LG=INT (A/2)+1:RG=A 
 10050 IF RG<=1  THEN 10190 
 10060 IF LG<=1  THEN 10100 
 10070 REM AUFBAU DES HAUFENS 
 10080 LG=LG-1 
 10090 I=LG:GOTO 10140 
 10100 REM WEGNEHMEN DES MAXIMUMS 
 10110 S$=A$(1)=A$(1)=A$(RG):A$(RG)=S$ 
 10120 RG=RG-1 
 10130 I=1 
 10140 X$=A$(I) 
 10150 P=0:REM FLAG FUER NICHT GEFUNDEN 
 10160 IF 2*I<=RG AND P=0  THEN 10200 
 10170 A$(I)=X$ 
 10180 GOSUB 3000: GOTO 10050 
 10190 GOTO 10300: REM ENDE 
 10200 REM FELDVARIABLE A$(I) EINORDNEN 
 10210 J=2*I 
 10220 IF J<RG  THEN IF A$(J)<A$(J+1) THEN J=J+1 
 10230 IF X$>=A$(J)  THEN 10260 
 10240 A$(I)=A$(J) 
 10250 I=J:GOTO 10160 
 10260 P=1:REM FLAG FUER PLATZ GEFUNDEN 
 10270 GOTO 10160 
 10280 : 
 10290 : 
 10300 REM ENDE