Logeleien (Teil 2)
Was hat es mit dem AND, dem OR und dem selten benutzten WAIT im Basic auf sich? Das und noch einiges mehr wird uns in dieser zweiten Folge der Logeleien beschäftigen.
In der täglichen Umgangssprache verwenden wir oft das Wörtchen »und«. Häufig wird es dabei genauso gebraucht wie ein logisches AND (siehe Bild 1).
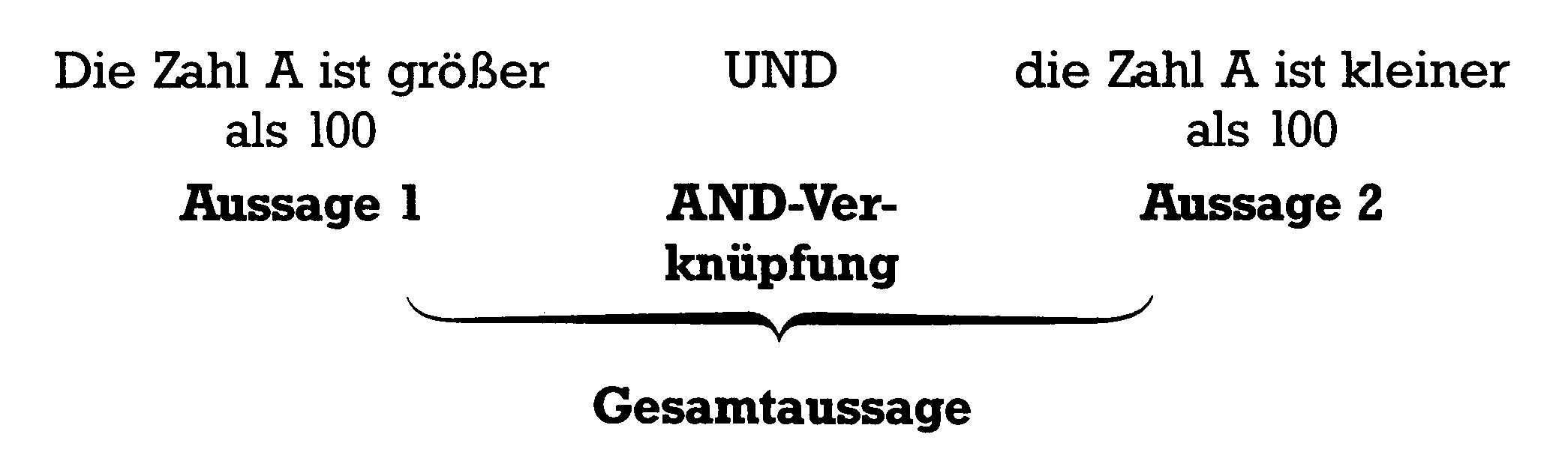
Wir sehen zwei Aussagen, die durch AND zur Gesamtaussage verknüpft wurden. Unser Gefühl sagt uns, daß die Gesamtaussage falsch ist, obwohl eine von den Einzelaussagen richtig sein kann. Sind beide Aussagen falsch (wenn A = 100), dann ist auch die Gesamtaussage falsch. Nur wenn beide Aussagen richtig wären, wäre auch die Gesamtaussage wahr. Sehen wir uns dazu die Wahrheitstabelle an (Tabelle 1).
| A1 | A2 | A1 AND A2 |
| W | W | W |
| W | F | F |
| F | W | F |
| F | F | F |
In den linken Spalten stehen untereinander alle möglichen Kombinationen der Wahrheitswerte von Aussage 1 (A1) und Aussage 2 (A2). Die rechte Spalte zeigt das Ergebnis der AND-Verknüpfung, das wir aus unserem Textbeispiel gewonnen haben.
Eine andere — ebenfalls bei der Verknüpfung von nur zwei Aussagen häufig gebrauchte — Darstellungsform einer Wahrheitstabelle zeigt Ihnen die Tabelle 2.
| A1↓ A2→ | W | F |
| W | W | F |
| F | F | F |
Hier werden in der linken Spalte die möglichen Wahrheitswerte der einen, in der Kopfzeile die der anderen Aussage eingetragen. Kreuzweise verknüpft man diese dann (hier also durch die AND-Verknüpfung) miteinander, was die quadratische Matrix der Wahrheitswerte der Gesamtaussage ergibt. Welche von beiden Formen Sie verwenden, ist Ihrem Geschmack überlassen. Hat man allerdings mehr als zwei Aussagen zu verknüpfen, dann ist die erste Form überschaubarer.
Wie kann man AND mit Aussagen nutzen? Sehen wir uns zunächst ein einfaches Beispiel an:
10 INPUT C
20 A = (C>5):B = (C<10)
30 IF A AND B THEN PRINT"C LIEGT ZWISCHEN 5 UND 10":GOTO 50
40 PRINT"C IST KLEINER/GLEICH 5 ODER GROESSER/GLEICH 10"
50 END
Aus diesem simplen Beispiel kann man sehen, daß sich mittels AND-verknüpfter Aussagen eine Klassifizierung vornehmen läßt. Häufig stellt sich folgendes Problem: Eine große Anzahl durch irgendwelche Peripherie eingehender Werte (zum Beispiel Meßwerte von Rausch-Frequenzen oder ähnliche) soll in Klassen einsortiert werden, um beispielsweise eine Häufigkeits-Verteilungzu erkennen.
Der gesamte mögliche Frequenzbereich wird dann in sogenannte Klassengrenzwerte unterteilt, die man in ein Array A(N +1) einliest. Jeder eingehende Meßwert X wird dann klassifiziert, indem er die folgende Programmzeile durchläuft:
FOR 1 = 1 TO N:A = (X>A(I)): B = (X<A(I + 1)): IF A AND B THEN Z(I) = Z(I) + 1
Dabei ergibt sich im Array Z(N) schließlich die Häufigkeitsverteilung.
Zahlen mit AND verknüpfen
Ebenso wie bei NOT muß die AND-Verknüpfung von Zahlen wieder auf der Bit-Ebene beobachtet werden. Dementsprechend setzt sich die Wahrheitstabelle wieder aus den Binärziffern 0 und 1 anstelle der Wahrheitswerte F und W zusammen (siehe Tabelle 3).
| A1 | A2 | A1 AND A2 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Falls Ihnen die andere Form der Tabelle besser gefällt, finden Sie diese in Tabelle 4.
| A1↓ A2→ | 1 | 0 |
| 1 | 1 | 0 |
| 0 | 0 | 0 |
Nur wenn beide miteinander AND-verknüpften Bits den Wert 1 haben, ist auch das Ergebnis 1. Nun können Sie ein wenig probieren — mit Hilfe des in der letzten Folge gezeigten Hilfsprogrammes — welche Möglichkeiten die AND-Operation bietet.
Wie Sie bei Ihren Versuchen vielleicht bemerkt haben, eignet sich AND vor allem zum Löschen von Bits. Probieren Sie mal das folgende Beispiel aus:
| 1. Zahl: | 255 |
| 2. Zahl: | 4 |
Im Ergebnis sehen Sie, daß alle Bits der ersten Zahl gelöscht wurden, außer dem Bit 2 (nur dort wurden zwei Bits mit dem Wert 1 AND-verknüpft). Die zweite Zahl nennt man eine Maske. So eine Maske konstruiert man ganz gezielt für das Löschen von Bits durch eine AND-Verknüpfung. Man nennt sie daher auch eine »AND-Maske«. Wollen Sie also erreichen, daß in einer beliebigen vorhandenen Zahl X alle Bits bis auf das zweite gelöscht werden (wobei vorausgesetzt wird; daß überhaupt Bit 2 von X gesetzt ist), dann AND-verknüpfen Sie diese Zahl mit der AND-Maske 4.
Zur Frage der Anwendung: Es gibt im Commodore 64 eine ganze Anzahl sogenannter Kontrollregister, in denen jedes Bit eine bestimmte Rolle spielt. Beispielsweise steuert das Register 53269 das Ein- oder Ausschalten von Sprites. Soll von mehreren abgebildeten Sprites nun Sprite 2 abgeschaltet werden, dann erfordert das ein gezieltes Löschen des Bit 2 dieses Registers. Alle anderen Bits sollen unberührt bleiben. Die Maske muß also außer bei Bit 2 (das den Wert 0 haben muß) überall eine 1 enthalten:
1111 1011
Das ist die Dezimalzahl 251 (oder 255-4). Der Basic-Befehl lautet daher:
POKE53269,PEEK(53269)AND251
oder allgemein:
POKE53269,PEEK(53269)AND(255-N)
Dabei ist N die Nummer des zu löschenden Sprites. Sollen mehrere Bits gleichzeitig gelöscht werden, müssen in der AND-Maske einfach an den entsprechenden Stellen Nullen auftreten. Das dürfte nun kein Problem mehr für Sie sein.
Der Vollständigkeit halber sei abschließend noch erwähnt, daß in der Literatur für die AND-Verknüpfung manchmal der Begriff »Konjunktion« verwendet wird.
Auch hier soll uns ein umgangssprachliches Beispiel helfen (siehe Bild 2).
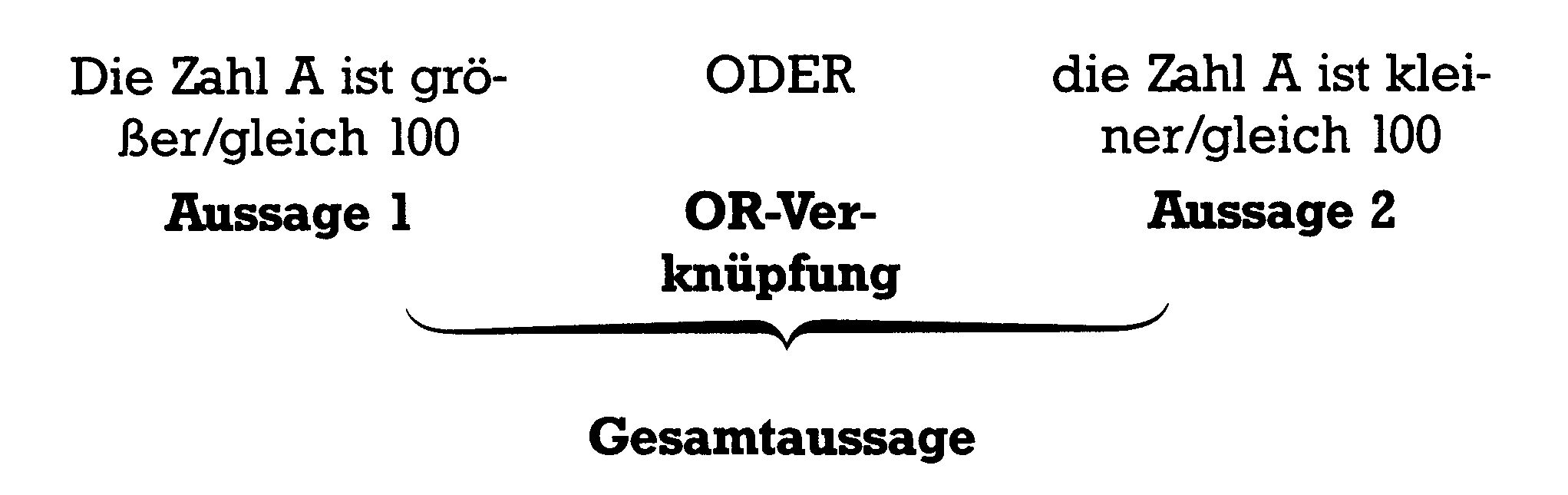
Die Gesamtaussage ist richtig, wenn mindestens eine der beiden Einzelaussagen wahr ist. Die Wahrheitstabelle verdeutlicht diese sogenannte OR-Verknüpfung (siehe Tabelle 5).
| A1 | A2 | A1 OR A2 |
| W | W | W |
| W | F | W |
| F | W | W |
| F | F | F |
Vielleicht ist Ihnen auch schon ein kleines Sprachproblem aufgefallen: Das Wort »oder« wird in zwei verschiedenen Bedeutungen gebraucht. Man unterscheidet:
- Inklusiv-Oder
Das ist das Oder, welches in diesem Abschnitt betrachtet wird, die OR-Verknüpfung.
- Exklusiv-Oder
Da haben wir ein anderes Oder, das wir noch untersuchen werden. In der normalen Sprache kann man es am besten durch »entweder…oder« umschreiben. In der mathematischen Logik- und in Programmierer-Kreisen nennt man es EOR oder manchmal auch XOR.
OR-verknüpfte Aussagen finden gerne Anwendung bei Menüabfragen. Es sei beispielsweise ein Menü mit fünf Optionen gegeben, das mittels GET abgefragt werde. Dann kann die entsprechende Zeile lauten:
100 GET A:IF A<1 OR A>5 THEN 100
Für viele von Ihnen ist das vermutlich ein alter Hut. Aber es gibt vielleicht doch auch einige Leser, die noch verwenden:
100 GET A:IF A = "" THEN 100
110 IFA = 1 THEN…
120 IFA = 2 THEN…
160 GOTO 100
Zahlen OR-verknüpfen
Zum OR-Verknüpfen von Zahlen steigen wir wieder in die Bit-Ebene herab. Hier zunächst einmal die Wertetabelle (Tabelle 6).
| A1 | A2 | A1 OR A2 |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Nur dort also, wo beide miteinander OR-verknüpften Bits gleich Null sind, wird auch das Ergebnis eine Null. Gewissermaßen haben wir hier das Gegenteil der AND-Verknüpfung vorliegen.
Das drückt sich auch in der Anwendung aus: Die OR-Operation kann zum gezielten Setzen von Bits verwendet werden. Auch das probieren Sie am besten mittels des Hilfsprogrammes aus. Gleichgültig, welche erste Zahl Sie angeben: Wenn Sie als zweite Zahl eine 4 (also 0000 0100) damit OR-verknüpfen, wird das Bit 2 des Ergebnisses auf 1 gesetzt sein. Alle anderen Bits bleiben unverändert erhalten. Die zweite Zahl ist hier wieder die Maske. Weil die Maske OR-verknüpft wird, spricht man von einer OR-Maske.
OR gibt uns die Möglichkeit, einzelne Bits in den Kontrollregistern zu setzen. So könnte man das vorhin (bei der Erklärung der AND-Operation) abgeschaltete Sprite wieder einschalten durch:
POKE53269,PEEK(53269)OR4
In der Literatur wird die OR-Operation häufig auch als »Disjunktion« bezeichnet.
Das exklusive Oder und Aussagen
NOT, AND und OR sind im Basic-Sprachvorrat enthalten. Die EOR-Operation ist in versteckter Form verfügbar und zwar im WAIT-Befehl. Bevor wir uns aber diesem zuwenden, soll erst einmal die EOR-Verknüpfung untersucht werden. Wir hatten vorhin schon angedeutet, daß EOR umgangssprachlich durch »entweder…oder« umschrieben werden kann. Ein Beispiel ist auch in Bild 3 zu sehen.
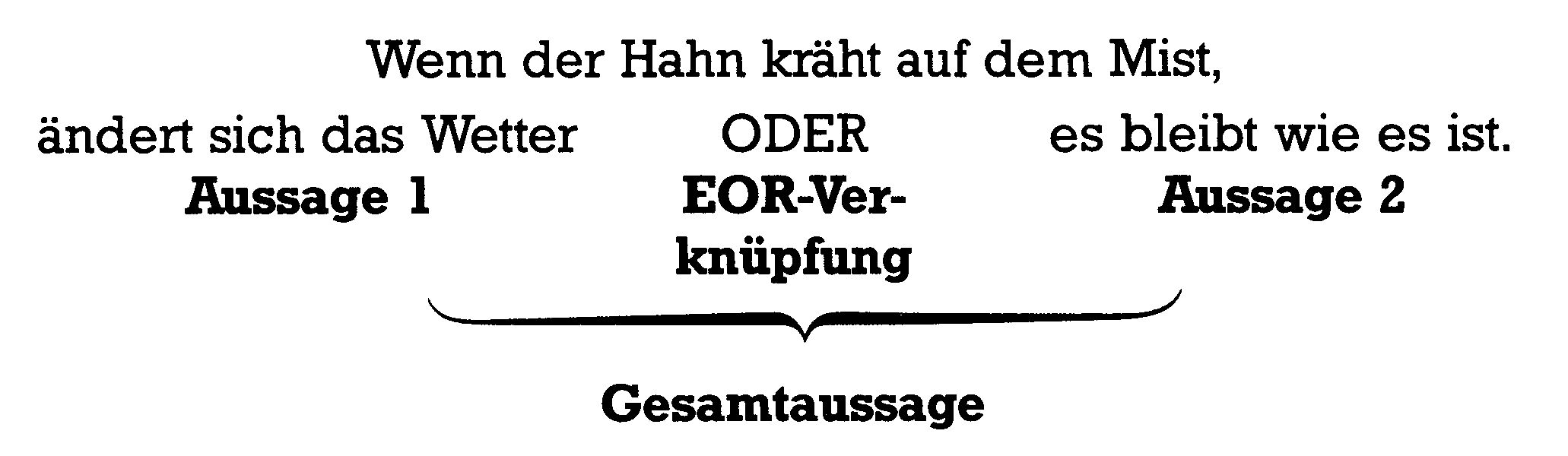
Immer dann, wenn nur eine der beiden Teilaussagen wahr ist, ist auch die Gesamtaussage richtig. Die Wahrheitstabelle zur EOR-Verknüpfung finden Sie als Tabelle 7. Sehen wir uns nun noch an, was die EOR-Operation mit Zahlen anrichtet.
| A1 | A2 | A1 EOR A2 |
| W | W | F |
| W | F | W |
| F | W | W |
| F | F | F |
Zahlen exklusiv »geODERt«
In unserem Hilfsprogramm ist auch diese Möglichkeit vorgesehen. Sie erkennen, wenn Sie die Option 4 einmal ausprobieren, daß die EOR-Operation bei zwei gleichen Bits immer 0, bei ungleichen immer 1 ergibt. Die Wahrheitstabelle sieht daher so aus, wie in Tabelle 8 gezeigt.
| A1 | A2 | A1 EOR A2 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Ein Fakt ist an der EOR-Operation interessant: Wendet man auf eine beliebige Zahl zweimal hintereinander dieselbe EOR-Maske an (muß ich nun sicher nicht mehr erklären, oder?), dann ist das Ergebnis wieder die Ausgangszahl. Probieren Sie es mal aus, zum Beispiel mit:
| 234 | ||
| 1. Mal | 56 | EOR |
| 210 | ||
| 210 | ||
| 2. Mal | 56 | EOR |
| 234 |
Damit haben wir die Voraussetzungen erfüllt, den WAIT-Befehl zu verstehen.
WAIT: Ein Aschenputtel in Basic
Wie es schon der Name sagt (wait = warten), hält WAIT ein Programm so lange an, bis in einer spezifizierten Speicherstelle ein bestimmtes Bit-Muster aufgetreten ist. Dieses Bit-Muster gibt man durch zwei Masken vor, von denen die erste (obligatorische) eine AND-, die zweite eine EOR-Maske ist. So sieht die Syntax des WAIT-Befehls aus:
WAIT Speicherstelle, AND-Maske, EOR-Maske
Der effektive Einsatz von WAIT erfordert eine recht gute Kenntnis der Speicherbelegung unseres Commodore 64, was vermutlich einer der Gründe für die seltene Benutzung dieses Befehls ist.
Wie eben schon kurz gesagt, kann WAIT mit einem oder mit zwei Argumenten betrieben werden. Sehen wir uns zunächst mal an, was mit nur einem Argument möglich ist.
Hier wird der in der adressierten Speicherstelle enthaltene Wert mit der AND-Maske verknüpft. Ergibt sich dabei ein Wert, der ungleich Null ist, dann fährt das Programm fort. Im anderen Fall wartet es, bis der Speicherinhalt dieser Anforderung entspricht (also bis irgendwann einmal die AND-Verknüpfung des Speicherinhaltes mit der AND-Maske keine Null mehr ergibt) oder aber bis man, des Wartens müde, das Programm durch RUN/STOP-RESTORE unterbricht. Sehen wir uns dazu ein praktisches Beispiel an. Vielfach werden Programme bis zu einem Tastendruck mittels:
100 GET A$:IFA$ = ""THEN 100
angehalten. Das hat den Nachteil, daß man dafür eine Basic-Zeile vergeben muß, was beispielsweise beim VC 20 in der Grundversion eine unverzeihliche Sünde sein kann. Statt dessen bedienen wir uns einer Speicherstelle in der Zeropage, die die Anzahl der gültigen Zeichen im Tastaturpuffer angibt: 198. Schreiben wir:
POKE 198,0:WAIT198,1
dann wartet das Programm, bis durch einen Tastendruck ein Zeichen im Tastaturpuffer aufgetreten ist. Diese Befehls-Sequenz kann nun auch mitten zwischen anderen Befehlen stehen. Was passiert dabei? Folgendes:
| Inhalt von 198 nach einem Tastendruck: | 0000 0001 |
| AND-Maske: | 0000 0001 |
| Ergebnis der AND-Operation: | 0000 0001 |
Das Ergebnis ist ungleich Null, das Programm läuft weiter.
Wenn wir WAIT198,2 eingeben, wartet das Programm auf zwei Tastendrucke. Was geschieht bei WAIT 198,3? Probieren Sie es aus: Schon nach dem ersten Tastendruck läuft das Programm weiter. Sehen wir uns mal an, weshalb. 3 sieht im Binärformat so aus: 0000 0011. Wenn nun nur ein Tastendruck in 198 registriert ist, ergibt die AND-Verknüpfung auch schon ein Ergebnis, das ungleich Null ist:
| 0000 0001 | Eine Taste | |
| 0000 0011 | Maske | AND |
| 0000 0001 |
Man kann also nur auf 1, 2, 4, 8 etc. Tastendrucke warten.
Ein anderes nützliches Beispiel ist die Speicherstelle 653, die die Kombinationstasten (SHIFT, Commodore und CTRL) überwacht. WAIT653,1 wartet auf die SHIFT-Taste, WAIT653,2 auf die Commodore-Taste und WAIT653,4 auf die CTRL-Taste.
Damit wollen wir für diesmal aufhören zu »logeln«. In der nächsten Folge geht es dann um den WAIT-Befehl mit zwei Argumenten. Außerdem werden wir feststellen, ob ein Computer auch Schlußfolgerungen ziehen kann.
(Heimo Ponnath/gk)