Logo
C 64
Grafik-Welt
9/85, S. 106-108

Streifzüge durch die Grafik-Welt (Teil 1)

Grafik ist für viele Computer-Freunde ein wahres Zauberwort und ein fast unerschöpfliches Thema. Wir stellen Ihnen ein Grafiksystem vor, mit dem Sie in Zukunft alle Programme des Kurses mit den verschiedensten Grafik-Hilfen verwenden können.

Zwar haben wir in all den bisherigen Folgen des Grafik-Kurses auch immer ein paar Programmbeispiele gezeigt, besonders in den letzten waren wir aber reichlich theoretisch. Und weil Sie ja nun sicherlich Hires-3 mal ausprobieren möchten, sollen diesmal einige Beispiele gezeigt werden. Außerdem muß unbedingt mal etwas gegen die Sprachverwirrung in Fragen der »Computergrafik« getan werden! Deshalb unternehmen wir den Versuch, dieses Feld etwas genauer zu beschreiben.

1. Was ist eigentlich Computergrafik?

Alle Welt spricht von Computergrafik, aber kaum jemand erklärt, was man darunter eigentlich zu verstehen hat. Sie werden sagen, daß das doch ganz einfach sei: Computergrafik ist Grafik, die mittels des Computers gemacht wird. Das betrifft dann beispielsweise Sprites oder Shapes, Filmgrafik wie in TRON, bewegten Hintergrund wie bei bestimmten Spielen, Konstruktionsverfahren mittels CAD, Auswertung von Satellitenaufnahmen durch Falschfarbenverfahren, Balkendiagramme aus kaufmännischen Anwendungen, Simulation von Dreikörperproblemen in der Physik, Untersuchung von dreidimensionalen Funktionen in der Mathematik, Identifizierung von Objekten per Computer, und so weiter. Ich hoffe, Sie haben bemerkt, daß wir da ein enorm breites Sammelsurium von Computergrafik haben. Es ist dringend nötig, irgendwelche Unterscheidungen zu treffen, Strukturen festzustellen. Zunächst einmal, »Computergrafik« sollte besser als grafische Datenverarbeitung bezeichnet werden und betrifft dann drei mögliche Kombinationen von Daten und Grafik:

  1. Zur Eingabe gelangen Daten, aus denen Bilder erzeugt werden. Das ist das, was wir künftig Grafik nennen werden. Dazu gehören dann beispielsweise Funktionenplots, Szenarios für Simulationen, etc.
  2. Bilder werden eingegeben und auch Bilder wieder erzeugt. Das ist die Aufgabe der Bildverarbeitung. Dazu gehören dann die Techniken, unterschiedliche Grauwerte mittels verschiedener Farben zu differenzieren oder mit einer Videokamera aufgenommene Bilder in irgendeiner Weise zu verfremden.
  3. Die Eingabe erfolgt als Bilder, die Ausgabe als Daten. Diesen Weg nennt man Bildanalyse und das ist ein aufstrebender Zweig beispielsweise der militärischen Satellitenerkundung. Dabei liegt die Aufgabenstellung darin, die Unzahl an Bildinformationen per Computer zu untersuchen auf bestimmte Objektklassen, zum Beispiel Schiffe oder ähnliches. Es ergeben sich sodann Daten, die weiterverarbeitet werden. Wie diese drei Gebiete zusammenhängen, zeigt Bild 1.
Bild 1. Das ist »Computergrafik«

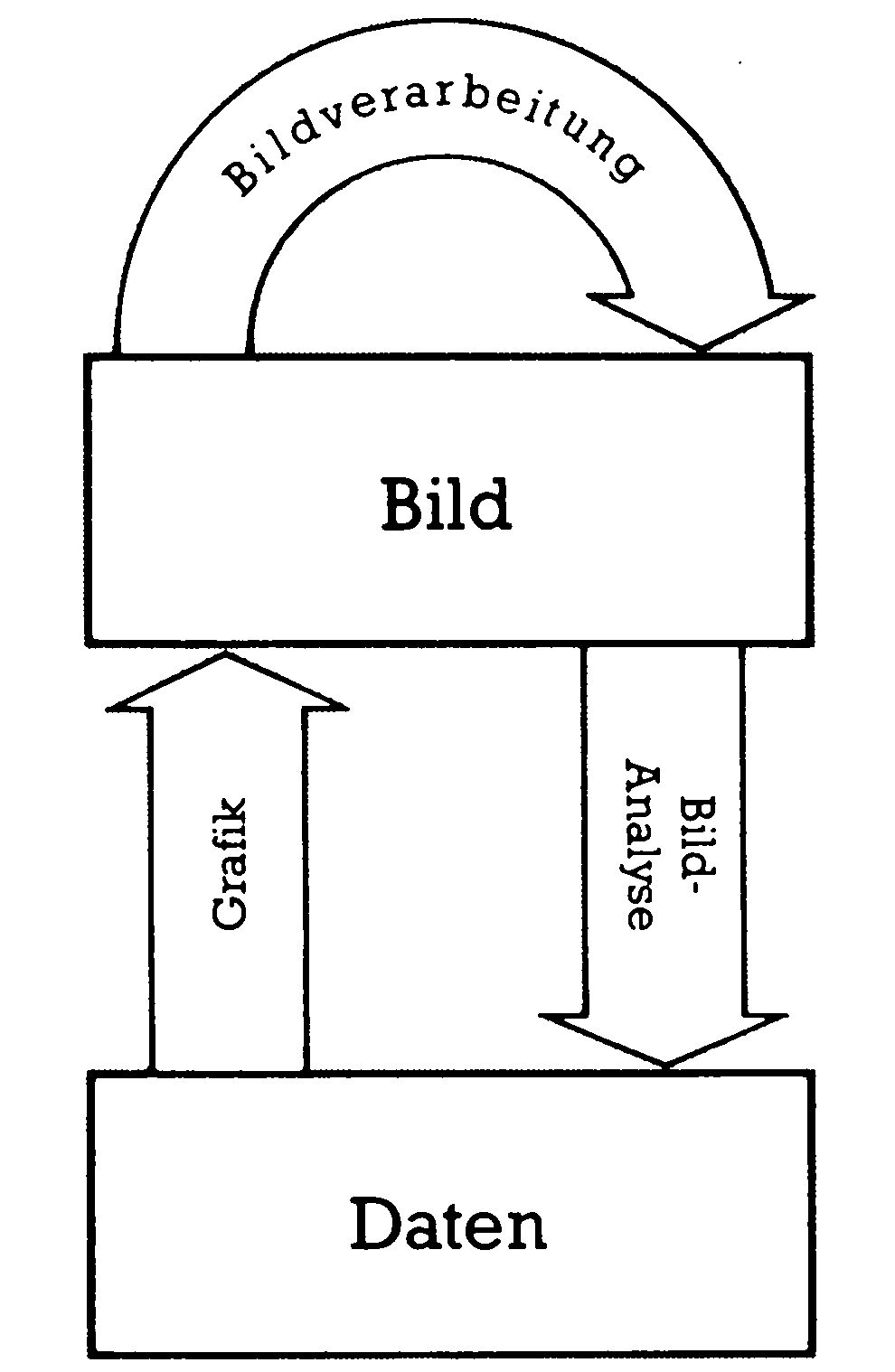
Es gibt viel Gemeinsames der drei Bereiche: Datenstrukturen, Speichern und Darstellen der Bilder erzeugen Aufgabenstellungen oder Lösungen, die identisch sein können. Ein Beispiel: In der Bildverarbeitung stellt sich häufig die Aufgabe, Konturen nachzuzeichnen. Andererseits erfordert die Grafik oft das Ausfüllen von umrandeten Flächen. Beide Problemstellungen sind entgegengesetzte Aspekte eines Problems und es läßt sich leicht verstehen, daß ein gemeinsames theoretisches Gerüst zur Lösung verwendet wird.

Nachdem wir diese grundsätzliche Unterteilung getroffen haben, können wir uns auf die Grafik selbst konzentrieren. Pavlidis [1] hat eine Unterscheidung von Bildern getroffen, die weniger mit dem Augenschein als vielmehr mit der Programmierung und Darstellungstechnik zu tun hat. Er teilt die Bilder in vier Klassen ein:

Klasse 1

Das sind Abbildungen mit einer vollen Grauskala oder Farbbilder. Ein gutes Beispiel bilden Fernsehaufnahmen. Die Darstellung erfolgt durch Integer-Werte, die als Bildelemente oder Pixels in Matrizen enthalten sind.

Klasse 2

Sogenannte »Bilevel-Bilder«, weil sie nur zwei Zustände kennen: Schwarz und Weiß. Ein Beispiel kann eine Textseite in einem Buch sein. Die Bildinformationen sind als Bits in einer Matrix enthalten.

Klasse 3

Hiermit sind Kurven und Linien, also kontinuierliche Punktfolgen erfaßt. Beispiele bilden Umrisse von Objekten oder Funktionsgraphen. Die Bildspeicherung kann auf verschiedene Weise erfolgen: Durch Erfassen der X-Y-Koordinaten oder durch Verkettungscodes etc.

Klasse 4

Gruppen diskreter Punkte, die zu weit auseinander liegen, um noch als Kurven beschrieben zu werden. Die Erfassung geschieht meist in Variablen-Feldern (Arrays).

Wie Sie unschwer erkennen werden, ist die Trennung der einzelnen Klassen nicht sehr scharf. Besonders die Grenzen zwischen Klasse 1 und Klasse 2 sowie zwischen Klasse 3 und Klasse 4 sind fließend. Bedingt durch technische Anforderungen, werden häufig Bilder einer bestimmten Klasse durch andere Klassen realisiert. Zum Verständnis sollen zwei Beispiele dienen:

Flächen höherer Ordnung sind eigentlich Klasse 1- oder 2-Abbildungen. Trotzdem werden sie oft als Klasse 3-Bilder, nämlich als eine Anzahl von Kurvenzügen dargestellt.

Hardwaremäßig ist der Commodore 64 auf Bilder der Klassen 1 und 2 zugeschnitten. Kurvenplots, die eigentlich Klasse 3-Bilder sind, müssen als Klasse 2-Abbildungen umschrieben werden. (Dazu kommen wir gleich noch)

Transformationen sind Übergänge zwischen verschiedenen Bezugssystemen. Ein Beispiel wäre die Transformation, die in Bild 2 anhand eines Überganges von einem Koordinatensystem zu einem anderen gezeigt wird.

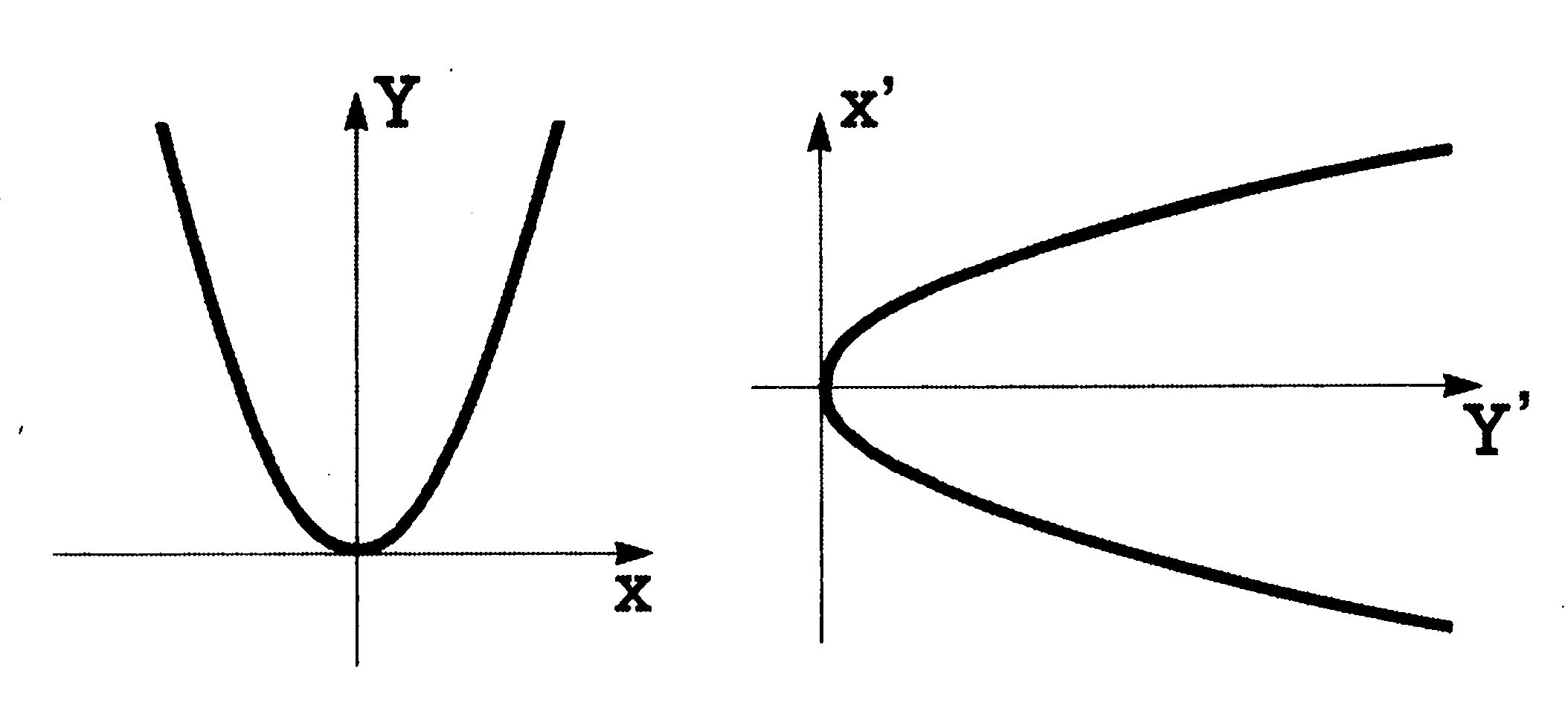
Bild 2. Beispiele für Transformationen

Auch zwischen den vier Klassen gibt es Möglichkeiten der Transformation, die in der grafischen Datenverarbeitung mit bestimmten Namen versehen sind:

Übergang zwischen den Klassen

Auch innerhalb der Klassen sind Transformationen von großer Bedeutung, sie werden uns noch häufig beschäftigen. Zunächst einmal gehören dazu Übergänge vom Räumlichen ins Flächenhafte: die sogenannten Projektionen. Der umgekehrte Weg wird übrigens Rekonstruktion genannt. Eng mit den Projektionen hängen die Probleme der Hinterschneidung zusammen, die wir im Grafik-Kurs, Folge 7 (64’er, Ausgabe 10/84) schon gestreift haben. Im englischen Sprachgebrauch unterscheidet man noch zwischen der »hidden line« und »hidden surface«- Problematik, was bedeutet »verborgene Linie« oder »verborgene Oberfläche«. Zu Transformationen innerhalb einer Klasse gehören auch Koordinatentransformationen, wie Drehung, Translation, Zerrung oder Stauchung von Systemen und natürlich die Übergänge zwischen verschiedenen Arten der Koordinatensysteme, wie kartesisch zu polar oder zylindrisch.

Bevor wir nun mit der Systematik der grafischen Datenverarbeitung weitermachen, brauchen wir noch einige Details über Bildeingabe und Bildwiedergabe.

2. Bildeingabe

Hauptsächlich bei der Bildverarbeitung und der Bilderkennung stellt sich das Problem der Bildeingabe. Wenn man allerdings den Grad der Interaktion bei der Grafikerstellung erhöht, sind auch dort Eingaben von Bildern denkbar. Zur Begriffsklärung: Interaktion nennt man das »Gespräch« zwischen Computer und Benutzer. So gibt es Programme, die auf einen Tastendruck ein fertiges Bild erstellen, ohne daß man — außer einem RUN/STOP — noch eine Eingriffsmöglichkeit hat. Andere erfragen ständig neue Eingaben, wie zum Beispiel die Joystickgrafik mittels des Programmes Hi-Eddi (Listing des Monats, 64’er, Ausgabe 1/85). Im ersten Fall ist der Grad der Interaktion gleich Null, im zweiten Fall ist er sehr hoch. Bei CAD-Anwendungen liegt ebenfalls ein hoher Interaktionsgrad vor und dort ist es bisweilen sinnvoll, ganze Bildteile nicht als Daten, sondern als Bilder einzugeben.

In jedem Fall stellt sich das Problem, ein analoges Bild in ein Feld diskreter Daten umzusetzen, es zu digitalisieren. Der Prozess des Digitalisierens besteht aus zwei Teilen, nämlich dem Segmentieren und dem Quantisieren der Abbildung. Segmentieren: Die gesamte Bildfläche muß in Bildpunkte (möglichst charakteristische) unterteilt werden. Man spricht hier von »Raumauflösung« des Bildes.

Quantisieren: Jedem so gewonnenen Bildpunkt wohnt eine Bildcharakteristik inne (zum Beispiel Grauwert), die nun als Zahl ausgedrückt wird. Man spricht von der »Grauwert- (oder auch Farbwert-) Auflösung.

Schwerwiegende Probleme gibt es eigentlich nicht beim Digitalisieren. Man könnte beispielsweise ohne weiteres eine Fernsehkamera einsetzen, die jedes Objekt in eine ganze Anzahl von Punktzeilen rastert — also eine hohe Raumauflösung liefert — und auch zwischen Weiß und Schwarz sehr viele Grauabstufungen erfaßt — also eine gute Grauwertauflösung erzeugt. Die Schwierigkeit liegt eher in der genügend schnellen Verarbeitung der dadurch erzeugten Informationsflut. Deshalb verwendet man im allgemeinen lieber spezielle Bilderfassungsgeräte, sogenannte Digitizer, die in ihrem Verfahren der jeweiligen Computergeschwindigkeit eher angepaßt sind. Mit Hilfe sogenannter »Scanner« (das heißt »Abtaster«) wird ein Bild in genau definierte Zeilen oder sonstige Punktfolgen zerlegt und dann quantisiert.

Ein anderes Verfahren sind die Tablett-Digitizer, wo beispielsweise die Wechselwirkung zwischen einer magnetisierten Oberfläche und einem elektrisch geladenen Stift ausgenutzt wird. Für die interaktive grafische Datenverarbeitung gewinnen diese Geräte mehr und mehr an Bedeutung.

3. Bildwiedergabe

Die Wiedergabe von Daten als Bild ist komplexer als die Bildeingabe. Hier muß nicht nur die Umsetzung digitaler in analoge Signale stattfinden, sondern auch noch eine Anpassung an die jeweiligen Hardware-Gegebenheiten. Bei diesen unterscheidet man von vornherein zwei: Hardcopy-Ausgabe und CRT-Ausgabe. (CRT = »cathode-ray-tube«, auf deutsch: Bildschirm). Eine Hardcopy erfordert lediglich die Anpassung der Daten an geräteabhängige Formate und die Einhaltung einer gewissen Reihenfolge der Datenübermittlung.

Die Bildschirmdarstellung verlangt das erstere auch. Die Besonderheit bei dieser Art der Bildwiedergabe ist aber, daß die gesamte Abbildung mindestens 30mal pro Sekunde an das Bildschirmgerät gesandt werden muß. Ein Bild entsteht ja durch die Wechselwirkung eines Kathodenstrahles mit einer phosphoreszierenden Schicht auf der Bildschirmplatte. Je nach Intensität des auftreffenden Strahles wird ein mehr oder weniger helles Aufleuchten eines Bildpunktes bewirkt. Das Nachleuchten dieser Schicht ist nur recht kurz, so daß der Bildinhalt häufiger aufgefrischt werden muß. Das menschliche Auge nimmt weniger als 25—30 Auffrischungen als Flackern wahr, daher also die Mindestzahl von 30 kompletten Bildübermittlungen pro Sekunde.

Für jeden Bildpunkt müssen mindestens drei Informationen an das Bildschirmgerät gesandt werden: Die X- und die Y-Koordinate, sowie die Intensität (also der Grauwert) des Strahles an der so spezifizierten Stelle. Bei Farbbildern sind es sogar fünf Informationen, denn anstelle des Grauwertes muß für jede Grundfarbe (drei davon gibt es) ein Wert übermittelt werden. Die Mischung dieser Farbinformationen führt dann zur jeweiligen Farbdarstellung. All dies nimmt uns beim Commodore 64 glücklicherweise der VIC-II-Chip in Zusammenarbeit mit den CIAs ab. Das ist zwar einerseits eine gewaltige Erleichterung für uns Benutzer, führt aber andererseits auch — wie wir gleich sehen werden — zu gewissen Einschränkungen.

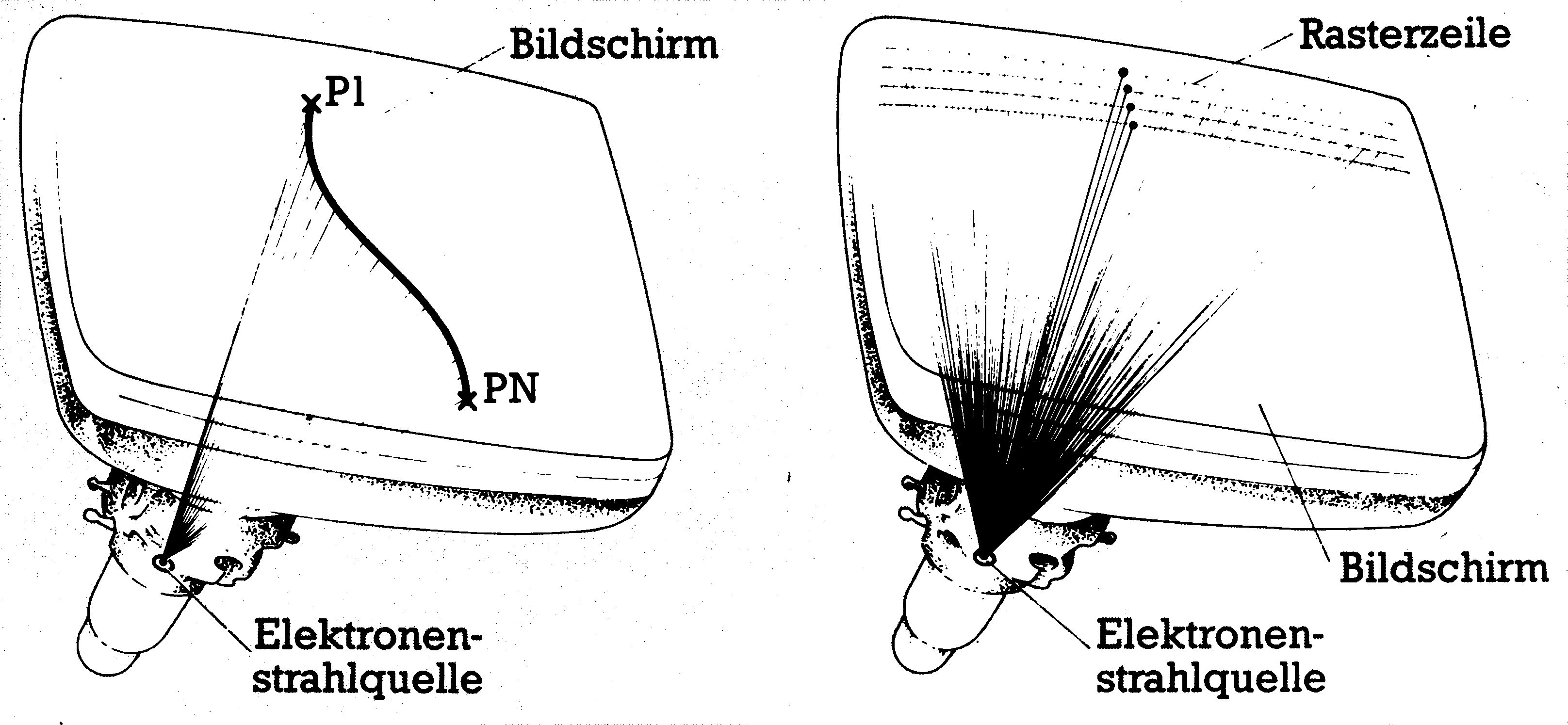
Man unterscheidet nämlich grundsätzlich zwei Verfahren der Bildwiedergabe per CRT-Gerät: Die Raster- und die Vektor-Methode. Sehen wir uns zunächst mal die Vektormethode an. Sie ist speziell für Bilder der Klassen 3 und 4 geeignet. Der Elektronenstrahl wird hier genau zum Punkt geführt, der durch die X- und Y-Koordinaten charakterisiert ist und an dieser Stelle dann einen Leuchtpunkt der gewünschten Intensität erzeugt. Alle anderen möglichen Bildschirmpositionen bleiben unberücksichtigt. Nehmen wir mal an, eine Abbildung setze sich zusammen aus der Punktfolge P1, P2, P3, …. Pn (siehe auch Bild 3).

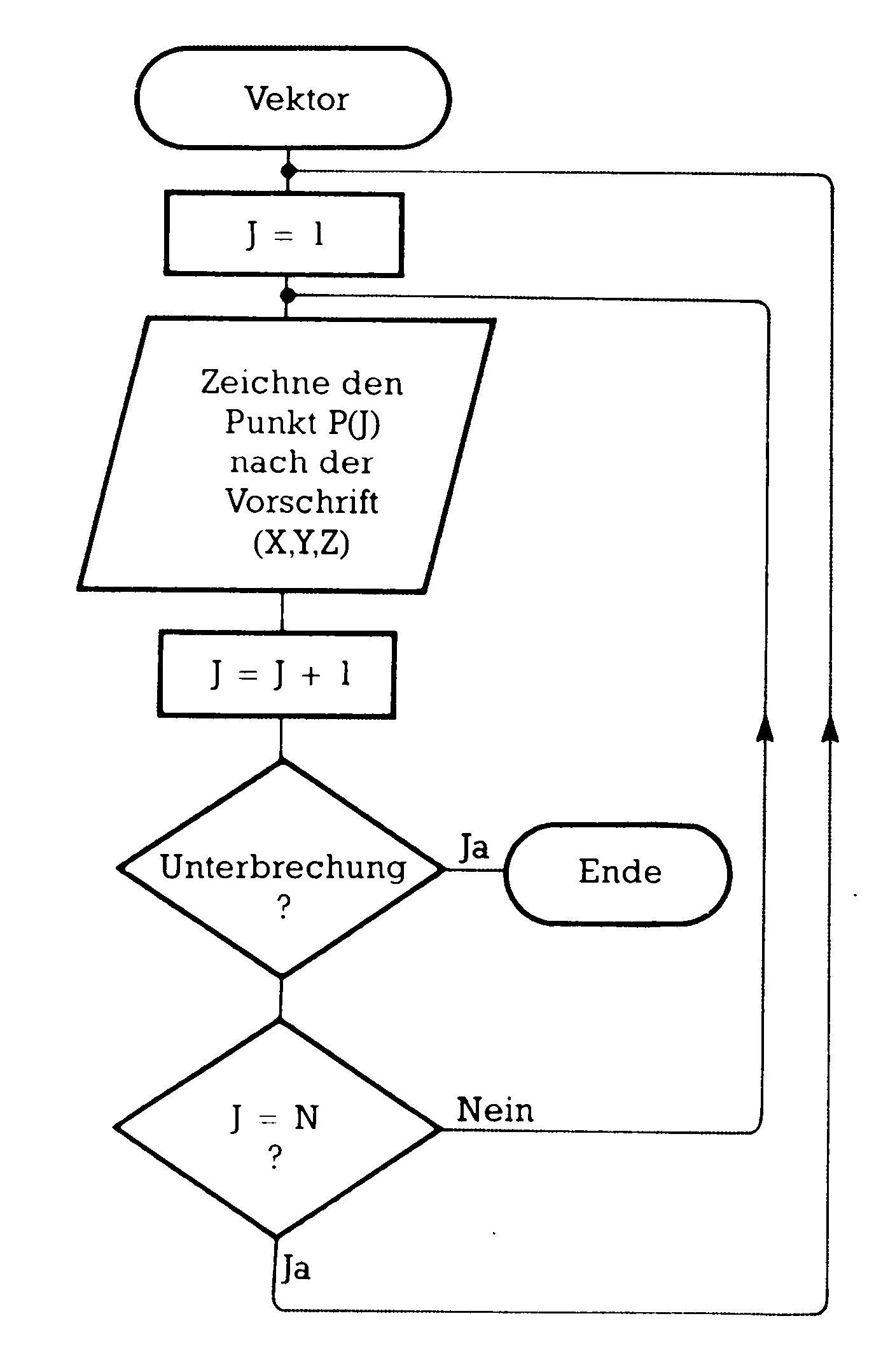
Bild 3. Bildschirmaufbau bei Vektorgrafik und Rastergrafik

Als Programm könnte man die Arbeit der Bildwiederholung dann etwa so schreiben:

Bild 4 zeigt einen Programmablaufplan dieser Routine. Was man gut erkennen kann: Der Elektronenstrahl durchläuft nur die Punktfolge. Will man einen Punkt entfernen oder ändern oder dazupacken, ist das ohne weitere Berücksichtigung aller anderen Punkte möglich. Die Bildwiederholung kann sehr schnell geschehen und ist abhängig von der Anzahl der zu bearbeitenden Punkte. Da sieht man dann auch gleich den Nachteil dieser Methode: Wenn die Abbildung sehr komplex wird, also beispielsweise ein Bild der Klasse 1 oder 2 auf diese Weise erzeugt werden soll, dann wird die Reihe der Punkte P(I) ziemlich lang und es kann in Grenzfällen zum Flackern des Bildes kommen. Der Vorzug dieses Verfahrens liegt darin, daß die Auflösung praktisch nur von den gerätetechnischen Details des Bildschirmgerätes abhängt. Übliche Auflösungen liegen bei etwa 4096x4096 Bildpunkten.

Bild 4. Flußdiagramm eines »Vektorgrafik-Programmes«

Was ist nun Rastergrafik? Jedem Ort auf dem Bildschirm entspricht hier ein Ort im Speicher des Computers. Besonders geeignet ist dieses Verfahren zur Darstellung von Bildern der Klassen 1 und 2. Aus der Speicheradresse folgt der Bildschirmort, aus dem Inhalt einer solchen Adresse der Grauwert, den der Kathodenstrahl an diesem Ort realisieren soll. Bei jeder Bildwiederholung wird der gesamte für diesen Zweck reservierte Speicher abgetastet und sein Inhalt an das Bildschirmgerät gesandt. Nehmen wir mal an, der Bildschirmspeicher sei 8000 Byte groß (N = 8000), dann könnte man hier ebenfalls ein Programm schreiben zur Bildwiederholung (siehe auch Bild 3).

Auch hier wieder ein Programm-Ablaufplan (Bild 5):

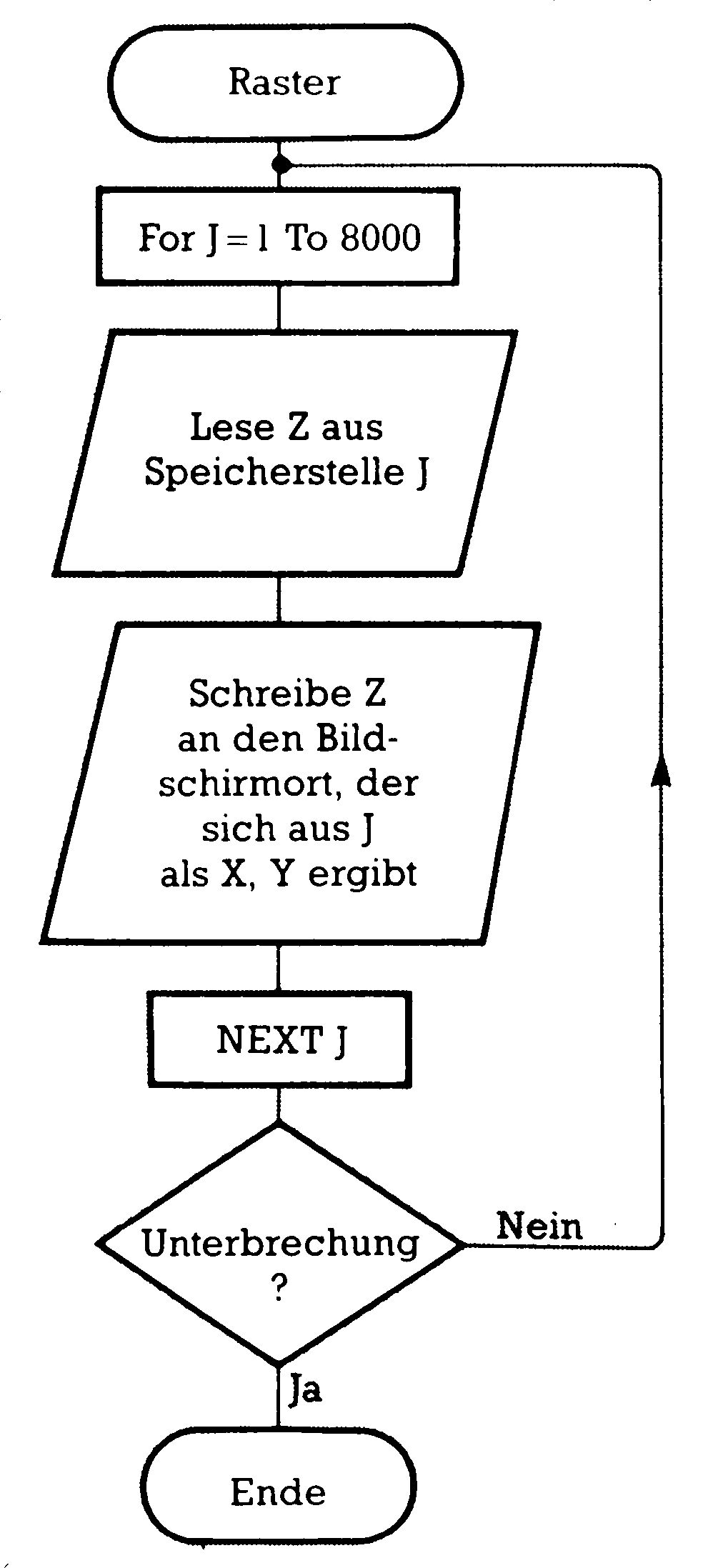
Bild 5. Bildschirmaufbau bei Rastergrafik

Es ist gleichgültig, ob nur ein einziger Punkt zu setzen ist oder alle: Jedesmal wird der gesamte Speicherinhalt übertragen, die Ausführungszeit ist also konstant und nur von der Auflösung — hier also der Speichergröße N — abhängig.

Der Umgang mit Rastergrafik ist komplizierter als der mit Vektorgrafik. Wenn sich beispielsweise zwei Abbildungsbereiche überlappen, darf man beim Rasterverfahren nicht einfach einen davon löschen, denn damit wirkt man auch auf die an derselben Stelle liegenden Teile des zweiten Bereiches ein. Die Vektorgrafik nimmt einfach die Punkte aus dem Auffrischungszyklus heraus, die zu löschen sind. Weil bei dem Rasterverfahren zwischen Bildschirm und Speicher ein 1:1-Verhältnis besteht, kommt man ziemlich schnell an die Grenzen der möglichen Auflösung. Schon eine Auflösung von 1024*1024 Pixels erfordert bei Klasse 2-Bildern (also mit einer Bit-Map) 128 KBytes Speicherraum. Nun werden Sie sagen, daß Speicherraum ja immer preiswerter zu haben ist und man deshalb ohne weiteres zu guten Auflösungen, die denen des Vektorverfahrens gleichkommen, gelangen könnte. Dabei wird aber übersehen, daß zum Beispiel diese ganzen 128 KByte innerhalb einer 30stel Sekunde durchgeblättert werden müssen. Nimmt man aber nur mal einen Lese- und Schreibvorgang — ohne auf die Feinheiten zu achten — wie zum Beispiel: LDA (Adresse 1),Y STA (Adresse 2),Y und sieht sich an, wieviel Zeit diese Sequenz braucht (nämlich etwa 11 Taktzyklen für ein Byte an Informationen), dann dauert das Lesen und Übertragen der ganzen 128 KByte immerhin schon 1 441 792 Taktzyklen und das muß auch noch mindestens 30mal in der Sekunde passieren! Außer einem großen Speicher ist somit auch ein sehr schneller Mikroprozessor vonnöten und genau da liegen die Grenzen dieses Verfahrens.

4. Standortbestimmungen

Nach all diesen Details können wir schonmal eine Standortbestimmung wagen: Unser Commodore 64 ist eingerichtet auf Rastergrafik. Er kann mit Hilfe des VIC-II-Chip den Inhalt einer 8000 Byte großen Bit-Map auf dem Bildschirm zeigen. Der 3. Wert, also der Grauwert Z, kommt aus einem weiteren 1000 Byte großen Speicher, wie Ihnen noch aus den ersten Folgen dieser Serie in Erinnerung sein dürfte. Der zu einer bestimmten Bildschirmposition gehörige Bitwert der Bit-Map sagt bei uns nur aus, ob das obere oder das untere Nibble des Grau- (oder Farb-) Codes aus dem 1000 Byte großen Speicher realisiert werden soll. Noch komplizierter ist der Multicolormodus, der uns den Übergang zu Klasse 1-Abbildungen ermöglicht.

Einige weitere Standortbestimmungen betreffen Hires-3 und unsere weiteren Grafik-Folgen. Wir werden uns nahezu ausschließlich der Grafik im engeren Sinn widmen, also der Wiedergabe von Daten als Bilder. Wegen der Auslegung von HiRes-3 und der besseren Auflösung beschränken wir uns auf Klasse 2 Abbildungen, wobei wir Klasse 3 und 4 nachbilden können bzw. auch Transformationen von Klasse 4 nach Klasse 3 und Klasse 2 durchführen werden. Transformationen innerhalb der Klassen werden in allen Formen auftreten (Projektionen, Rotationen etc.).

Zum Thema Interaktionsgrad: Wenn man eine Skala definieren würde, die von 100 Prozent Interaktion (zum Beispiel Erstellen einer Grafik per Lichtgriffel oder Grafik-Tablett) bis 0 Prozent (Einladen einer gespeicherten Grafik vom Massenspeicher) reichte, dann könnte man zum Beispiel Hi-Eddi zwischen 98 und 60 Prozent einordnen. Hires-3 bietet als Befehlsvorrat — je nach Einsatz im Programm — nahezu die gesamte Skala. Allerdings müßte man den Schwerpunkt der Interaktionsfähigkeit unterhalb von Hi-Eddi definieren, denn die Eingabemöglichkeiten per Joystick oder Lichtgriffel sind nicht besonders unterstützt, müssen also gesondert programmiert werden.

5. Systematik-Kauderwelsch

Kommen wir nun wieder zum Versuch zurück, grafische Datenverarbeitung zu strukturieren. Sinnvolle Unterteilungen der Grafik im engeren Sinn (Daten werden zu Bildern) hat kein Autor zu treffen versucht. Zu neu und in rasanter Entwicklung scheint dieses Gebiet zu sein.

Ich möchte deshalb nur auf zwei unvollständige Strukturen eingehen. Zum einen unterteilt man gerne nach dem Kriterium der Anwendung:

  1. Business-Grafik

    Dazu zählen zum Beispiel die allseits bekannten Balken-, Torten- und Liniendiagramme

  2. CAD = »Computer aided design«

    Darunter versteht man das Konstruieren mit Computerhilfe.

  3. Ein Sammelsurium weiterer Anwendungsbereiche wie:
    • Mathematische: Untersuchung von Funktionen, Lösungsmengen etc.
    • Statistische etc.: Operations Research, Meßwertverteilung, etc.
    • Künstlerische: Filmdesign, …
    • etc.

Aus der engen Verknüpfung von Grafik mit der Mathematik rührt eine andere Unterteilung her, die die Algorithmen und ihre Herkunft aus den mathematischen Teilgebieten als Kriterien hat:

  1. 2-dimensionale Grafik (2D)

    Analytische Geometrie der Ebene, ebene Transformationen, Approximationen, Schraffuren, etc.

  2. 3-dimensionale Grafik (3D)

    Analytische Geometrie des Raumes, räumliche Transformationen, Projektionen, hidden-line-Problem, etc.

Sie sehen sicher selbst, daß es äußerst schwierig scheint, hier in dieses Kauderwelsch eine gewisse Ordnung zu bringen. Wir werden in den weiteren Grafik-Folgen außer einigen grundlegenden programmtechnischen Details (wie zum Beispiel das »smooth scrolling«) Beispiele aus fast allen Gebieten erarbeiten.

Fortsetzung folgt

(Heimo Ponnath/gk)

Literatur:
[1] Theo Pavlidis: Algorithms for Graphics and Image Processing, Berlin-Heidelberg 1982: Springer-Verlag, ISBN 3-540-11338-X

PDF Diesen Artikel als PDF herunterladen
Mastodon Diesen Artikel auf Mastodon teilen
← Vorheriger ArtikelNächster Artikel →