Reise durch die Wunderwelt der Grafik (Teil 3)
In dieser Folge werden wir die ersten Schritte in das Reich der hochauflösenden Grafik wagen. Doch zunächst soll die Grafik etwas farbiger werden. Das heißt, wir erzeugen mehrfarbige Zeichen und variieren die Hintergrundfarbe.
Bevor wir die dritte Etappe auf dem Weg zur hochauflösenden Grafik beginnen, soll noch eine kurze Rückschau auf den in der letzten Folge bewältigten Weg gehalten werden: Wir können jetzt mit dem Binär- und dem Hexadezimalsystem umgehen und haben gelernt, wie man Zahlen darin ausdrückt. Wir haben gesehen, wie der Computer sich Adressen merkt und konnten mit diesem Wissen RAM-Bereiche schützen. Wir haben wichtige Zeiger in unserem Computer kennengelernt. Das Setzen oder Löschen von beliebigen Bits in einem Byte beherrschen wir ebenso wie die Definition und Benutzung eigener Zeichen. Wenn Sie seit der letzten Folge viel ausprobiert und so Übung gewonnen haben, dann kennen Sie Ihren Computer schon ganz gut.
Heute werden wir zunächst etwas mehr Farbe ins Spiel bringen, indem wir mehrfarbige Zeichen oder Zeichen mit einem anderen Hintergrund benutzen. Dann betreten wir das Gemach von Dornröschen (der hochauflösenden Grafik) und küssen es wach — im übertragenen Sinne natürlich. Nach dieser Ankündigung sind die ersten schon aufgebrochen. Also gehen wir auch los.
Erinnern Sie sich bitte an Bild 11 aus der letzten oder an Bild 8 aus der ersten Folge. Egal, ob es sich um Zeichen aus dem Zeichen-ROM oder um selbstdefinierte Zeichen handelt, eines haben sie gemeinsam: Überall dort, wo sich im Bit-Muster des Zeichens eine 1 befindet, also ein Bit gesetzt ist, taucht bei der Darstellung auf dem Bildschirm ein Punkt in der Zeichenfarbe auf, die im Bildschirmfarbspeicher angegeben ist. Diese Farbe haben wir entweder im Direktmodus durch Drücken der »CTRL«- oder »COMMODORE«-Taste in Kombination mit einer Zifferntaste festgelegt oder durch ein »POKE 646, Zeichenfarbe« oder auch durch POKEn eines Farbcodes in die entsprechende Stelle des Bildschirmfarbspeichers.
Überall dort, wo im Bitmuster des Zeichens eine 0 ist, taucht bei der Darstellung auf dem Bildschirm nichts auf, das heißt dort erscheint die Farbe des Bildschirmhintergrundes. Jedes Bit aus dem Bit-Muster wird also im Normalbetrieb und auch bei selbstdefinierten Zeichen einzeln interpretiert. Es gibt nun auch andere Möglichkeiten der Interpretation des Bit-Musters, und eine davon wird im Mehrfarbenmodus angewendet. Hier sind die Bits des Zeichens zu Paaren zusammengefaßt (Bild 1).
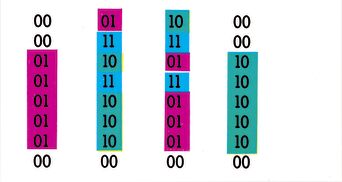
Das ist der Buchstabe »A« mit paarweise zusammengefaßten Bits. Es ergeben sich vier verschiedene Möglichkeiten der Bit-Kombination: 00, 01, 10, 11
Erinnern Sie sich an die Binärzahlen, dann erkennen Sie, daß diese vier Möglichkeiten den Zahlen 0, 1, 2, 3 entsprechen. Sie wirken wie Zeiger, die in verschiedene Register des VIC-II-Chip deuten (Tabelle 1; siehe auch Registerübersicht in der ersten Folge).
| Bit-Paar | Register # | Bit-Paar zeigt auf: | |
| Adresse | Bedeutung | ||
| 00 | 33 | 53281 | Hintergrundfarbe Nr. 0 |
| 01 | 34 | 53282 | Hintergrundfarbe Nr. 1 |
| 10 | 35 | 53283 | Hintergrundfarbe Nr. 2 |
11 bringt die Farbe, die in Bit 0 bis 2 des Bildschirmfarbspeichers vorhanden ist
Dort also, wo ein Bitpaar 00 steht, wird es in der Farbe des Bildschirmhintergrundes angezeigt, wie bisher im Normalmodus mit einem Bit 0 geschehen. In Adresse 53281 haben wir bisher ja immer schon die Bildschirmfarbe festgelegt. Hinzu kommen die Register 34 und 35 des VIC-II-Chips entsprechend den Adressen 53282 und 53283. Hier können wir nun weitere Farben eingeben, die an den Stellen auf dem Bildschirm gezeigt werden, an denen die dazugehörige Bit-Kombination (01 oder 10) steht. Erlaubt sind alle Farben (0 bis 15).
Nun sind es noch zwei Voraussetzungen, die uns vom Mehrfarben-Zeichen trennen: Dem Computer muß mitgeteilt werden, daß er das Bit-Muster in Paaren statt einzeln interpretieren soll. Das geschieht dadurch, daß man im Register 22 (Adresse 53270) das Bit 4 auf 1 setzt. Falls Sie sich nicht mehr so genau erinnern, wie wir sowas in der letzten Folge gemacht haben — hier ist es nochmal gezeigt (Bild 2).

Es muß also eingegeben werden:
POKE 53270,PEEK(53270) OR 16
Dieses Byte 53270 im VIC-II-Chip ist ein Beispiel dafür, wie sorgfältig man auf das richtige Setzen oder Löschen von Bits achten sollte. Wenn Sie sich die Registerübersicht in der 1. Folge und dort besonders dieses Byte ansehen, stellen Sie fest, daß fast jedes Bit eine andere Funktion zu erfüllen hat.
Sollten Sie die obige Basic-Zeile im Direktmodus eingegeben haben, dann verwandeln Sie alle Buchstaben auf dem Bildschirm in mehrfarbige Zeichen. Auf einem Schwarzweiß-Gerät sind sie dann kaum mehr zu erkennen. Hier stellt man auch den Unterschied zwischen einem Farbfernseher und einem Farbmonitor fest. Der letztere trennt die unterschiedlichen Farben deutlich voneinander, während auf dem Fernsehschirm häufig Farbmischungen auftreten. Deswegen sollte die Farbgebung in die Register 34 und 35 individuell ausfallen: Probieren, probieren …
Das Ausschalten des Mehrfarb-Zeichen-Modus geschieht durch Löschen des Bit 4 in 53270 mit
POKE 53270, PEEK(53270) AND 239.
Falls Sie vorhin beim Anschalten des Mehrfarb-Modus nicht die normale Zeichenfarbe (Code 14), sondern eine zwischen 0 und 7 vorliegen hatten, dann haben Sie keine Veränderung bemerkt.
Und damit sind wir bei der zweiten Voraussetzung: Es kommt nämlich auch noch auf den Inhalt jeder Bildschirmfarbspeicherstelle an (55296 bis 56295). Erst wenn für eine solche Zelle das Bit 3 gesetzt ist (= 1), findet man Zeichen im dazugehörigen Bildschirmplatz in der Mehrfarbdarstellung. Sehen wir uns dazu noch einige Farbcodes an:
1 = bin. 0001 7 = bin. 0111 Bit 3 ist gelöscht 8 = bin. 1000 15 = bin. 1111 Bit 3 ist gesetzt
Der Farbcode bewirkt also zweierlei:
a) Er gibt an, ob ein Zeichen im Mehrfarbmodus dargestellt wird, und
b) er verleiht den Bit-Paaren »11« die Farbe.
Zur Demonstration können Sie ja mal folgendes Programm eingeben:
10 PRINT CHR$(147) 20 POKE 53281,6:POKE 53282,1:POKE 53283,0:REM LADEN DER 3 FARBREGISTER 30 POKE 53270,PEEK(53270)OR 16:REM ANSCHALTEN DES MEHRFARBEN-MODUS 40 POKE 646,0:REM ZEICHENFARBE AUF 0(BLK) 50 PRINT CHR$(17)"JETZT IST DER MEHRFARBENMODUS":PRINT "EINGESCHALTET" 60 PRINT CHR$(17)"IN DIE BILDSCHIRMFARBZEILEN IST ABER DIE";:PRINT"0 EINGEGEBEN" 70 PRINT CHR$(17)"DESWEGEN IST DIE ZEICHENDARSTELLUNG";:PRINT"NORMAL" 80 POKE 646,14:REM ZEICHENFARBE AUF 14(HBLU) 90 PRINTCHR$(17)"DER FARBCODE IST JETZT 14" 100 PRINT CHR$(17)"DER MEHRFARBEN-MODUS IST SICHTBAR" 110 END 120 POKE 53270,PEEK(53270)AND239:REM AUSSCHALTEN DES MEHRFARBEN-MODUS 130 END
Wenn dieses Programm mit Zeile 110 beendet ist, befinden Sie sich weiterhin im Mehrfarbenmodus und können nach Herzenslust durch POKE 646, »Zeichenfarbe«, oder mit »CTRL«-beziehungsweise »COMMODORE«-Taste und einer Zifferntaste die Zeichenfarbe ändern und den Effekt beobachten. Übrigens ist der Cursor unterhalb der READY-Meldung noch da — was Sie durch eine Änderung der Zeichenfarbe sofort feststellen können. Sollten Sie genug von diesem Modus haben, dann geben Sie ein CONT »RETURN« und das Programm schaltet wieder den Normalmodus ein.
Sollten Sie zufällig mal durch
PRINT PEEK(53281),PEEK(53282), PEEK(53283)
in die Hintergrundfarbregister sehen, dann werden Sie dort nicht — wie im Programm veranlaßt — die Ziffern 6,1,0 sehen, sondern 246,241,240. Das liegt daran, daß die Bits 4 bis 7 dieser Register für die Farbgebung nicht benutzt werden und vom Betriebssystem auf 1 gehalten werden. Die Binärzahl 1111 0000 entspricht dem Dezimalwert 240. Deswegen muß man zur Farbcodezahl diese 240 addieren, um den Speicherinhalt zu erhalten.
Wieder eine andere Art der Interpretation findet man beim Modus für erweiterte (oder veränderte) Hintergrundfarben. Damit kann man zum Beispiel ein grünes Zeichen mit rotem Hintergrund auf einem gelben Bildschirm darstellen. Hier wird der Bildschirmcode des Zeichens auf eine vom Normalmodus unterschiedliche Weise gelesen. Bit 7 und Bit 6 der Bildschirmcodezahl geben nämlich jetzt einen Zeiger auf Farbregister ab. Das geschieht in der Weise, wie in der Tabelle 2 gezeigt wird.
Beispiel »A«
| Zeichen | Codebereich | Code dezimal | Code, binär 76543210 |
Bit 6/7 | Hintergrundfarbregister | |
| Nr. | Adresse | |||||
| Normale Zeichen | 0-63 | 1 | 00000001 | 00 | 33 + 0 | 53281 |
| <SHIFT>-Zeichen | 64-127 | 65 | 01000001 | 0 1 | 33 + 1 | 53282 |
| Reversed Zeichen | 128-191 | 129 | 10000001 | 1 0 | 33 + 2 | 53283 |
| Reversed <SHIFT>-Zeichen | 192-255 | 193 | 11000001 | 1 1 | 33 + 3 | 53284 |
Es zeigt sich, daß nur 64 Zeichen dargestellt werden können — also keine Grafikzeichen. Verwendet man das normale A (Bildschirmcode 1), dann zeigen die Bits 7 und 6 auf das normale Hintergrundregister 53281. Verwendet man das geshiftete A (Bildschirmcode 65), verändert sich die Hintergrundfarbe des A (nicht das Zeichen selber) auf den Farbcode, der in 53282 steht. Ähnlich verläuft es mit dem reversen A (Bildschirmcode 129) und dem reversen geshifteten A (Bildschirmcode 193). In die Register 53281 bis 53284 können alle Farbcodes eingegeben werden.
Damit der Computer die Codes in dieser besonderen Weise liest, muß ihm das angezeigt werden, indem man im Byte 53265 das Bit 6 auf 1 setzt. Das sollten Sie schon können:
POKE 53265,PEEK(53265)OR 64
Das Abschalten dieses Modus geschieht durch Löschen des gleichen Bits:
POKE 53265,PEEK(53265)AND 191
Die Zeichenfarbe bleibt von der ganzen Umstellung unberührt. Man kann sie auf die nun schon bekannte Weise jederzeit ändern.
Warum kann man eigentlich in diesem Modus nur 64 Zeichen darstellen? Die Antwort darauf liegt darin, daß nur die Bits 0 und 5 für den Zeichencode zur Verfügung stehen, also
von 00 0000 ≙»@«
bis 11 1111 ≙»?«
mit Hintergrundfarbe aus 53281
Jede weitere Erhöhung beeinflußt die Bits 7 und 6, wird aber in den unteren 6 Bits nicht mehr wahrgenommen. Dort beginnt einfach die Zählung wieder ab 0:
(1)00 0000 = 64,
das bedeutet Zeichen 0 (@) mit Hintergrundfarbe aus 53282.
Ganz nett wäre es ja eigentlich, wenn man sowohl den Modus mit erweiterten Hintergrundfarben als auch dem Mehrfarbzeichenmodus miteinander kombinieren könnte. Jeder Versuch, das zu tun, endet mit einem schwarzen Bildschirm ohnejegliches Zeichen. An diese Möglichkeit haben die Schöpfer des VIC-II-Chip offenbar nicht gedacht.
Betrachten Sie jetzt doch einmal das nachfolgende Demonstrationsprogramm. Vor der Eingabe schalten Sie bitte durch gleichzeitiges Drücken der »COMMODORE«- und »SHIFT«-Tasten den Kleinschriftmodus ein.
5 print chr$(147) 10 poke53281,6:poke53282,0:poke53283,7:poke53284,10:rem laden der farbregister 20 poke53265,peek(53265)or64:rem anschalten des modus 30 print chr$(17)"der modus ist eingeschaltet aber der" 31 print"zeichencode ist kleiner als 64" 40 printchr$(17)"JETZT WIRD MIT GESHIFTETEN ZEICHEN":print"GEDRUCKT" 50 printchr$(17)chr$(18)"der druck mit reversed zeichen hat die" 60 printchr$(18)"hintergrundfarbe von register 53283" 70 printchr$(144)chr$(17)chr$(18)"REVERSED UND GESHIFTETE ZEICHEN" 80 printchr$(154):end 90 poke53265,peek(53265)and191 100 end
Ebenso wie beim vorigen Programm können Sie nach dem ersten END in Zeile 80 noch mit den verschiedenen Kombinationen von Zeichenfarbe und Zeichencode herumexperimentieren. Wenn Sie genug davon haben, erreicht ein CONT »RETURN« die Rückkehr in den Normalzustand.
Auch dieser Modus ist mit selbstdefinierten Zeichen ebenso verwendbar wie mit den ROM-Zeichen.
Wir betreten Dornröschens Schloß: Das Bit-Mapping-Prinzip
Es ist soweit! Wir stehen an der Schwelle zur hochauflösenden Grafik. Wenn wir bisher mit Zeichen aller Art auf dem Bildschirm gearbeitet haben, waren diese immer durch acht Bytes definiert: entweder durch das Zeichen-ROM oder durch einen von uns erstellten alternativen Zeichensatz im RAM. Jeder Aufruf eines Zeichencodes füllte einen Bildschirmspeicherplatz, zum Beispiel 1024 mit diesem Zeichen, also mit 8 Byte. Zugriff auf einzelne Byte hatten wir nur beim Selbstdefinieren, aber dieser Zugriff legte dann eben in der Anwendung auch wieder 8 Byte auf einmal fest. Wenn es nun eine Möglichkeit gäbe, ständig Zugriff auf einzelne Bytes zu haben und die Punktmuster jedes Bytes verändern zu können, dann hätten wir ganz andere Aussichten (Bild 3).
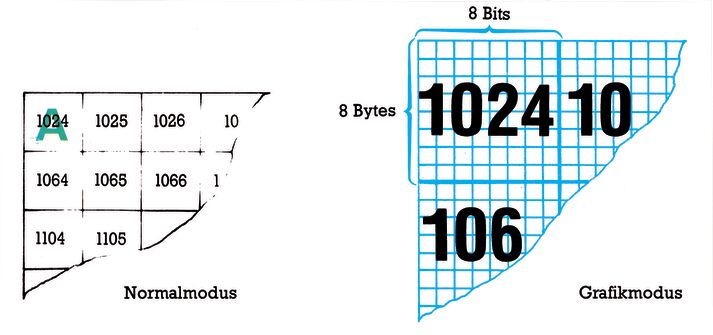
Überlegen wir mal: Statt 1000 Byte (40 x 25) hätten wir dann 8000 Byte (40 x 25 x 8) zu je 8 Bit, also insgesamt 64000 Bildpunkte, die ansprechbar wären! Genau das geschieht beim sogenannten Bit-Mapping. Der Computer legt sich gewissermaßen eine Landkarte dieser 8000 Byte an und bildet ihren Inhalt auf dem Bildschirm ab. Auf dem Bildschirm können wir mit dieser Karte nun (siehe Bild 3) in der Senkrechten (y) 25 x 8 = 200 Positionen und in der Waagerechten (x) 40 x 8 = 320 Positionen ansprechen. Immer dann, wenn ein Bit in der Bit-Map gesetzt (= 1) ist, erzeugt das automatisch das Aufleuchten eines der 64000 Bildpunkte auf dem Bildschirm. Ist ein Bit gelöscht (= 0), dann ist der Bildpunkt leer (siehe Bild 4).
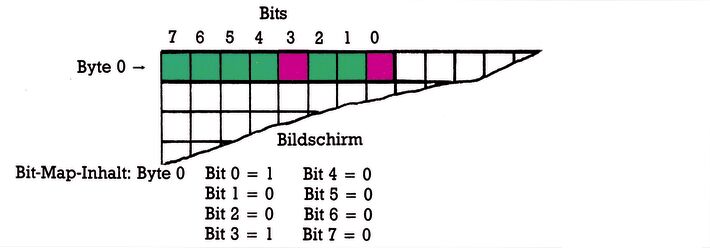
Dornröschen erwacht
Das Anschalten dieses Bit-Map-Modus ist der Kuß, den wir Dornröschen geben. Seien Sie nicht vorzeitig enttäuscht. Dornröschen hat 1000 Jahre geschlafen und wir müssen mit viel Geduld ihre Fähigkeiten nach und nach entwickeln helfen. Wenn Dornröschen jetzt erwacht, ist es hilflos wie ein neugeborenes Kind. Nach dieser Warnung also gehen wir so vor: Im VIC-II-Chip Register 53265 setzen wir Bit 5 auf 1, indem wir den Befehl
POKE 53265,PEEK(53265)OR 32
eingeben. Danach sieht der Bildschirm allerdings recht merkwürdig aus. Das ist auch kein Wunder, denn wie gesagt wird jetzt der Inhalt der Bit-Map dargestellt, und wir haben dem Computer noch nicht mitgeteilt, wo die Bit-Map zu finden ist. Das geschieht durch Setzen des Bit 3 des VIC-II-Registers mit der Adresse 53272 auf den Wert 0 oder 1. Dabei gelten die Zusammenhänge nach Tabelle 3.
| Bit 3 von 53272 | Ort der Bit-Map (Adressenbereich) |
| 0 | 0 - 7999 |
| 1 | 8192 - 16191 |
Der normale Inhalt von Byte 53272 ist 21 (das kennen wir noch aus der letzten Folge). Binär ausgedrückt ist das: 0001 0101
Bit 3 ist also 0. Alles, was in diesem Bit-Map-Speicherbereich von 0 (Zeropage!) bis 7999 (mitten im Basic-RAM) existiert, wurde beim Anschalten des Bit-Map-Modus abgebildet. Und weil die Zeropage laufend vom Betriebssystem für seine ständigen Arbeiten verwendet wird, sind im oberen Bereich unseres seltsamen Bildes auch flimmernde Stellen zu sehen — wo also laufend Bits gesetzt und gelöscht werden. Sehen Sie sich Ihren Bildschirm mit diesem merkwürdigen Abbild noch etwas genauer an. Etwa von der Mitte an sehen Sie Zeichen abgebildet. Dort liegt die Speicherzelle 4096, von der an das Geisterbild der Zeichen (siehe Folge 1) liegt. Wir sehen also Gespenster!
Nun sollten Sie mit »RUN/STOP« und »RESTORE« wieder den Normalzustand herstellen. Dann schalten Sie mit folgenden Programmen den Hochauflösungsmodus und die spezielle Bit-Map ab 8192 an:
10 PRINT CHR$(147):POKE53265, PEEK(53265)OR 32 20 POKE 53272,PEEK(53272)OR 8
Der letzte Befehl besorgt das Setzen des Bit 3 auf 1. Außerdem fügen wir vorsorglich noch die Rückkehr in den Normalmodus an:
110 POKE 53265,PEEK(53265)AND 223
Löschen des Bit 5 in 53265,
120 POKE 53272,PEEK(53272)AND 247
Löschen des Bit 3 in 53272.
Dazu bauen wir noch eine GET-Abfrage ein:
100 GET A$:IF A$ =”” THEN 100
Starten Sie jetzt mit RUN. Die Bit-Map ab 8192 wird auf dem Bildschirm gezeigt. Das ist leerer Speicher, so wie wir ihn in Form von Zahlen (Blöcken von 0 und 255) schon in der 1. Folge kennengelernt haben.
Die ersten Schritte
Sie erinnern sich vielleicht auch daran, daß manchmal, wenn auch selten, andere Zahlen eingestreut waren. Deswegen sieht man hier auch nicht immer ganz schwarze oder ganz helle Blöcke, sondern häufig welche mit Einsprengseln. Überall dort, wo ein Byte der Bitmap den Wert 255 hat, steht ja binär 1111 1111, das heißt 8 Bildpunkte auf dem Bildschirm sind angeschaltet. Wir sehen schon, wir müssen den Speicher noch löschen, also überall 0 hinschreiben:
30 B=8192:FOR I=0 TO 7999:POKE I + B,0:NEXTI
Wenn Sie diese Programmzeile noch einfügen und dann mit RUN starten, können Sie dem Computer bei der Arbeit zusehen.
Jetzt kommt Farbe ins Bild
Vermutlich sind Sie jetzt enttäuscht. Ein leerer schwarzer Bildschirm ist nicht gerade eindrucksvoll. Deswegen wollen wir nun noch zwei Dinge lernen: Wie kommt Farbe ins Bild und wie bekomme ich Punkte auf den Bildschirm?
Wenn Sie vor der Zeile 100 im Programm einen Stop-Befehl einfügen , tauchen nach der Abarbeitung der ersten Zeilen plötzlich farbige Quadrate auf dem Bildschirm auf. Die Antwort auf die Frage nach der Herkunft dieser Quadrate birgt für uns zugleich die Möglichkeit der Farbgebung. Geben Sie nun ein: CONT »RETURN«. Auch das erscheint als Folge farbiger Quadrate. Jetzt wartet der Computer auf einen Tastendruck, der auf dem Bildschirm folgendes erscheinen läßt:
BREAK IN 40 READY CONT READY □
Der Mehrfarbenmodus wird entschleiert
Genau an derselben Stelle waren im HIRES-Modus die farbigen Quadrate zu sehen. Die Farbe wird also anscheinend vom Inhalt der Bildschirmspeicherzellen gesteuert. Das B von BREAK hat einen Bildschirmcode von 2. Zwei ist auch der Farbcode für Rot. Falls Sie einen Farbmonitor Ihr eigen nennen, sehen Sie im Hochauflösungsmodus an der Stelle des B ein rotes Quadrat. Des Rätsels Lösung sieht so aus: Die Farbe des Hochauflösungsbildes wird von 8x8-Bit-Feldern gesteuert, die den Bildschirmspeicherzellen entsprechen. Die Steuerung ist also vom Inhalt des Bildschirmspeichers abhängig, nicht vom Inhalt des Farbspeichers. Schreiben wir zum Beispiel in Zelle 1024 eine 1, dann erhalten wir im Hochauflösungsmodus ein weißes Feld in der linken oberen Bildschirmecke. Nun wollen wir in diesen Bereich auch noch eine kleine Linie zeichnen: Löschen Sie bitte zunächst mal den STOP-Befehl und fügen Sie ein:
40 POKE 1024,1:POKE 8193,255
Nach dem Starten erhalten wir — wie erwartet — das weiße Feld links oben und darin einen schwarzen Strich. Um offen zu sein — ganz so erwartet war’s ja nicht. Denn woher hätten wir wissen können, daß der Strich schwarz ist? Sehen wir uns den Inhalt der Speicherzelle 1024 genauer an. Im binären System geschrieben steht dort jetzt:
0000 0001 MSN LSN = 0 = 1 N = Nibble (4 Bit)
Das legt die Vermutung nahe, daß die Hintergrundfarbe durch das LSN (hier 1 = weiß) und die Punktfarbe durch das MSN (hier 0 = schwarz) gesteuert wird. Probieren wir es einfach mal aus. Wir tauschen das ganze mal um und schreiben in 1024 den folgenden Wert:
0001 0000 MSN LSN = 1 = 0 (dezimal 16)
Also ändern wir in der Zeile 40 den ersten POKE-Befehl um in POKE 1024,16. Es klappt! Nach dem Starten (wie immer in diesem Programm nach einigem geduldigen Warten) erscheint ein weißer Strich auf schwarzem Grund. Nun können wir dieses triste Schwarz gezielt entfernen und von vornherein bestimmen, welche Farbe unsere Punkte bekommen sollen und welche der Hintergrund, indem wir in die Bildschirmzellen den Dezimalwert unserer Binärzahl eingeben. Damit Sie nicht jedesmal umrechnen müssen, hier eine nützliche Formel:
Farbkennziffer (F) = Zeichenfarbe (ZF) x 16 + Hintergrundfarbe (HF)
Zum Ausprobieren ändern wir unser Programm um:
5 INPUT"ZF,HF=";ZF,HF
In Zeile 40 schreiben wir jetzt neu:
40 F = ZF*16 + HF:FOR I = 1024 TO 2023:POKE I,F:NEXT I 50 POKE 8193,255
Wenn Sie beispielsweise nach dem Starten für die Zeichenfarbe 14 und für die Hintergrundfarbe 6 wählen, können Sie mit etwas Geduld wieder dem Computer bei der Arbeit zusehen und dann einen hellblauen Strich auf blauem Grund finden.
Dornröschen lernt zeichnen: Punkte setzen im Hochauflösungs-Modus
Wir sind es jetzt leid, immer einen fast leeren Bildschirm anzusehen. Ob er nun schwarz oder blau ist: Wir wollen nun auch mal etwas darauf sehen! Die Schwierigkeit liegt gar nicht darin, daß wir nicht wüßten, wie wir Punkte auf den Bildschirm kriegen. Wir müssen ja nur ein Byte im Bereich von 8192 bis 16191 mit ein paar gesetzten Bits versehen, zum Beispiel durch POKE 12000,1, und schon sehen wir einen Punkt. Das Problem liegt vielmehr darin, daß wir einen Weg finden, gezielt Punkte an bestimmte Orte des Bildschirms zu setzen. Dazu müssen wir den Aufbau der Bit-Map kennen und und ihren Zusammenhang mit dem Bildschirm. Das Prinzip ist in Bild 5 gezeigt.
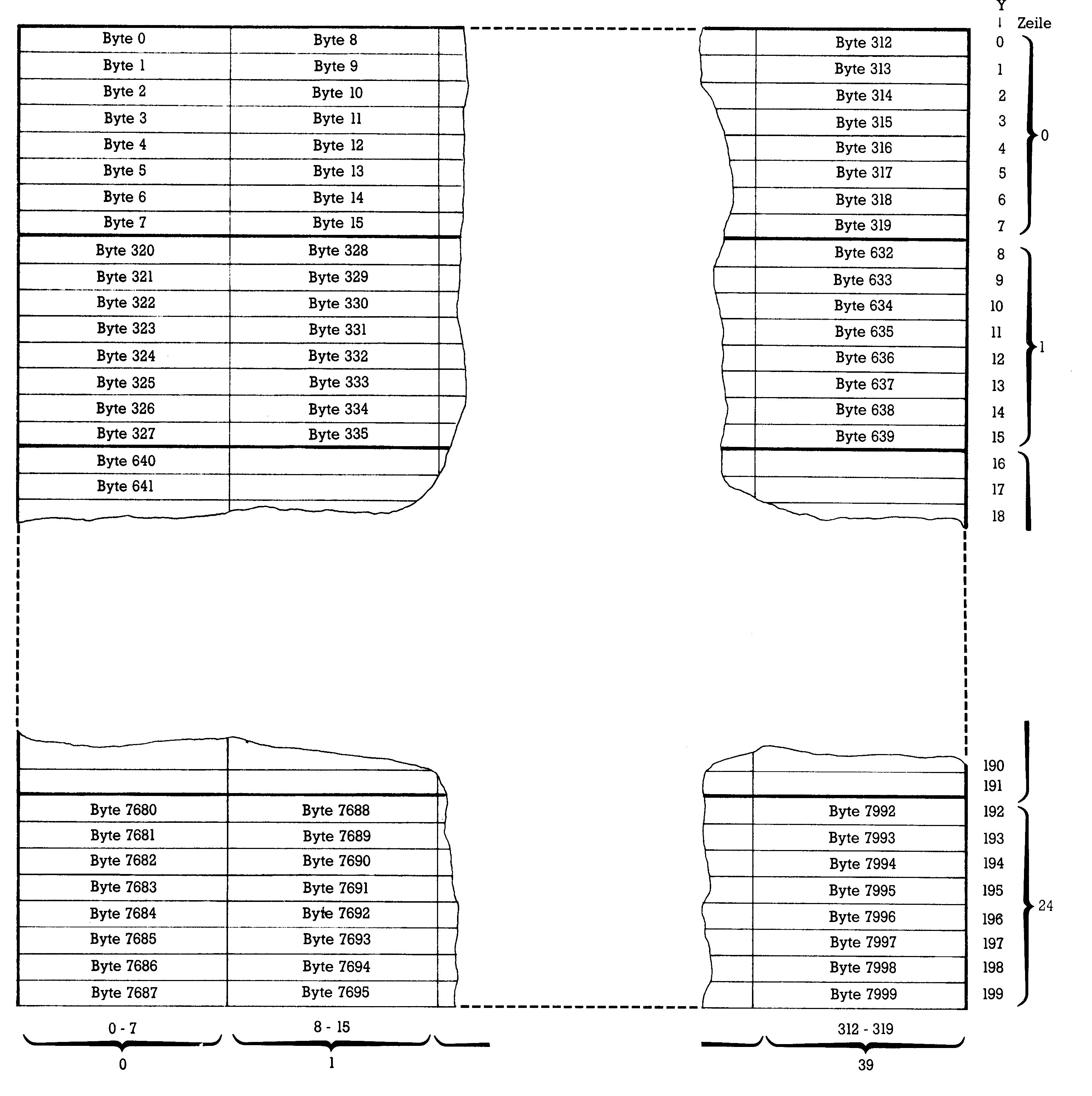
Die Speicherzellen der Bit-Map sind also angeordnet wie ein vollgeschriebener Bildschirm. Dort hatte ja jeder Buchstabe seine 8 Byte im Punktemuster. Aus der Anordnung ergibt sich außerdem, daß wir in der Y-Richtung 200 mögliche Positionen (0 bis 199) und in der X-Richtung 320 (0 bis 319) finden. Wir haben somit Bildschirmkoordinaten (Bild 6) und können Punkte definieren, zum Beispiel im Bild 6 den Punkt P mit den Koordinaten X = 110 und Y=100.
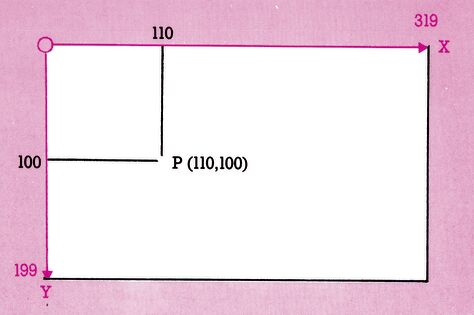
Wir wissen nur noch nicht, in welchem Byte wir welches Bit setzen müssen, um diesen Punkt zu sehen. Betrachten wir dazu Bild 5 genauer. Die 25 Bildschirmzeilen und die 40 Spalten sind noch erhalten. Jeder solche Bildschirmplatz besteht aus acht Byte mit je acht Bit. Stellen wir zunächst einmal fest, um welche Zeile es sich handelt:
Z=INT(Y/8)
Beispiel: Z=INT(100/8)=12
(Zeile 12)
Dann ermitteln wir die Spalte, in der unser Punkt liegt:
S=INT(X/8)
Beispiel: S=INT(110/8)=13
(Spalte 13)
In unserem Beispiel muß der Punkt in Zeile 12 an Spaltenplatz 13 stehen. Weil in jeder Zeile 320 Byte (8x40) und an jedem Platz 8 Byte vorhanden sind, fängt unser Bildschirmfeld bei Byte Nr.
Z*320 + S*8 = 12*320 + 13*8 = 3944 an (siehe Bild 7).
Nun müssen wir feststellen, um welches Byte in diesem Feld es sich handelt. Wir haben vorhin beim Feststellen der Zeile einfach gleich INT(Y/8) berechnet. Wenn wir nun nur Y/8 berechnen, kommen wir in unserem Beispiel auf Y/8 = 100/8 = 12.5. Ziehen wir davon INT(Y/8) ab: Y/8-INT(Y/8 = 12.5-12 = 0.5 und multiplizieren das Ergebnis mit 8:
80*(Y/8-INT(Y/8))=8*0.5=4
Genau das ist unser gesuchtes Byte: Nr. 4 von oben. Das sieht komplizierter aus, als es ist. Aus alledem ergibt sich jetzt, in welchem Byte der Bit-Map ein Bit zu setzen ist:
BYTE=Z*320 + S*8 + 8*(Y/8-INT(Y/ 8))
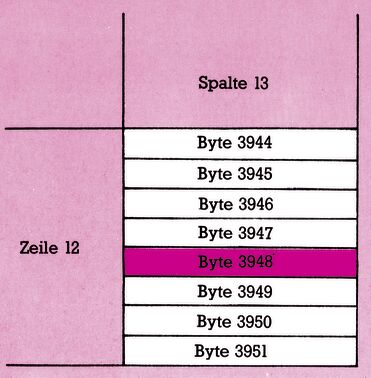
In unserem Beispiel ist es dann also das Byte 3948 der Bit-Map. Nun müssen wir noch herauskriegen, welches Bit in diesem Byte zu setzen ist (siehe Bild 8).

Auch hier haben wir vorhin bei der Berechnung der Spalte einfach gerechnet INT(X/8). Jetzt rechnen wir:
X-8*INT(X/8)=110-8*INT(110/8)
Das ergibt 6. Wenn wir das von 7 abziehen (Nummer des höchstwertigen Bit), erhalten wir:
BIT = 7-(X-8*INT(X/8))
Die Zauberformeln
In unserem Beispiel ist BIT = 1. Es muß also Bit 1 gesetzt werden. Damit haben wir jetzt folgende Formeln zur Verfügung:
BYTE=INT(Y/8)*320 + INT(X/8)*8 + 8*(Y/8-INT(Y/8))
und
BIT=7-(X-8*INT(X/8))
Den ersten Ausdruck für Byte kann man noch etwas vereinfachen:
BYTE = 8*(39*INT(Y/8) + INT(X/8) + Y/8)
Die genaue Speicherzelle ergibt sich durch Addieren der Bit-Map-Startadresse (8192) zu BYTE. Um also einen Punkt zu setzen, gibt man das Kommando:
POKE 8192 + BYTE,PEEK(8192 + BYTE) OR (2↑BIT)
Wir ergänzen jetzt unser Programm. Die Zeile 50 wird neu:
50 BY= 8*(39*INT(Y/8) + INT(X/8) + Y/8):BI = 7-(X-8*INT(X/8))
Dann folgt:
60 POKE B + BY,PEEK(B + BY) OR (2↑BI)
Außerdem müssen wir natürlich Punktkoordinaten eingeben:
6 INPUT"X,Y=";X,Y
Dabei ist darauf zu achten, daß X zwischen 0 und 319, Y zwischen 0 und 199 liegt. Starten Sie mit RUN, geben Sie die Koordinaten ein und nach einiger Weile wird Ihr Punkt auf dem Bildschirm zu sehen sein.
Auf eines sollten Sie noch achten, wenn Sie die Bit-Map bei 8192 beginnen lassen (in der nächsten Folge werden wir andere Möglichkeiten kennenlernen): Schützen Sie die Bit-Map vor dem Überschreiben durch Basic! Der verbliebene Speicherplatz für Basic-Text, Variable, Arrays, Strings ist so knapp, daß Sie ganz schnell die Bit-Map überschreiben. Deswegen sollten Sie (siehe Folge 2) eingeben:
POKE 51,255:POKE 52,31:POKE 55,255:POKE 56,31
Es ist geschafft: Die erste Grafik
Alles, was wir bis jetzt über die Hochauflösungsgrafik gelernt haben, soll hier nochmal als kleines Demonstrationsprogramm zusammengefaßt werden. Also NEW eingeben und dann:
10 POKE51,255:POKE52,31:POKE55,255:POKE56,31
20 ZF=0:HF=6:F=16*ZF+HF
30 DEFFNA(X)=50*SIN(X/30)+100
40 PRINTCHR$(147)
50 POKE53265,PEEK(53265)OR32
60 POKE53272,PEEK(53272)OR8
70 B=8192:FORI=0TO7999:POKEB+I,0:NEXTI
80 FORI=1024TO2023:POKEI,F:NEXTI
90 FORX=0TO319:Y=FNA(X)
100 BY=(XAND504)+40*(YAND248)+(YAND7):BI=7-(XAND7)
110 POKEB+BY,PEEK(B+BY)OR(2{$EE}{CBM-U}{YEL}BI):NEXTX
120 GETA$:IFA$=""THEN120
130 POKE53272,PEEK(53272)AND(255-8)
140 POKE53265,PEEK(53265)AND(255-32)
150 PRINTCHR$(147)
Dieses Programm setzt 320 Punkte nach der Form einer Sinus-Funktion. Zur Erläuterung sei noch bemerkt, daß in Zeile 100 eine etwas elegantere Lösung der Berechnung von BYTE und BIT angeführt ist. Sie können aber genauso gut die bisher verwendete benutzen. In Zeile 150 wird der Bildschirm nochmal gelöscht, denn bei der Eingabe der Farben haben wir ja die Bildschirmzellen mit einem Zeichencode belegt, der im Normalmodus immer unter dem Cursor sichtbar wäre.
Dornröschen ist also erwacht und hat die ersten zaghaften Schritte getan. Alles geht noch etwas langsam vor sich. Besonders das Löschen der Bit-Map (Programmzeile 70) erfordert geduldiges Abwarten — jedenfalls solange wir in Basic arbeiten. Für heute haben wir genug getan. Die nächste Folge wird ebenfalls der hochauflösenden Grafik gewidmet sein. Wir hauchen ihr weiterhin Leben ein.
(Heimo Ponnath)