Reise durch die Wunderwelt der Grafik
Sie lernen in diesem Kurs nicht nur etwas über die Grafik. Ausführlich erläutert werden auch die beiden wichtigsten Zahlensysteme für den Computer, das Binär- und das Hexadezimalsystem. Wir ermöglichen Ihnen Änderungen an der Speicherorganisation und bringen Ihnen die logischen Verknüpfungen naher. Und das alles, um schließlich eigene Zeichen erstellen zu können.
Die zweite Etappe unseres Weges durch das Bytegewirr zu unserem Dornröschen (der hochauflösenden Grafik) wird gleich gestartet. Wir sollten uns nochmal in Erinnerung rufen, was wir bisher gesehen haben. Da war zunächst mal ein Überblick über die gesamte Speicherorganisation unseres Computers. Genauer haben wir uns dann die Ein- und Ausgabebausteine angesehen, um schließlich einen Plan der VIC-II-Chip-Register zu finden. Wir haben das Rätsel teilweise gelöst, wie ein bestimmtes Zeichen an einen bestimmten Ort des Bildschirmes gelangt und woher unser Computer überhaupt weiß, wie beispielsweise das A aussehen soll. Dabei sind wir bereits allerlei Merkwürdigkeiten begegnet: Wir gehen durch Alices Wunderland! Nun, der Wunder sind's noch nicht genug gewesen, denn auch auf dieser Etappe werden wir allerlei Eigenartigkeiten sehen: Wir treffen die Zweifingerlinge und die Sechzehnfingerlinge. Wir werden lernen, wie wir unseren Computer hinters Licht führen können. Schließlich werden wir uns wie Frankenstein — aber besser als er — an neue Kreationen heranwagen. Die Pause ist beendet, wir brechen auf.
Im Grunde genommen haben sie uns schon fast die ganze 1. Folge über ungesehen begleitet: Die Zweifingerlinge. Um sie für uns sichtbar zu machen, bedarf es eigentlich nur einiger Gedankenübungen. Beobachten Sie mal kleine Kinder beim Zählen oder Rechnen: Das läuft Finger für Finger.
Wir haben zehn davon (im allgemeinen) und haben deswegen wohl auch neun Ziffern und die Null:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Um eine Zahl auszudrücken, die größer als 9 ist, zum Beispiel 9 + 1, setzen wir einfach zwei von diesen Ziffern zusammen und fangen wir wieder bei der kleinsten Ziffer 1 an und hängen eine Null dran: 10. Auf diese Weise können wir jeder Anzahl von Dingen eine Zahl zuordnen. Was wäre, wenn wir nur zwei Finger hätten? Wir hätten dann — wie die im Computer herumwimmelnden Zweifingerlinge — nur zwei Ziffern: 1 und 0.
Die Begegnung mit den Zweifingerlingen: Das Binärsystem
Um nun eine Zahl auszudrücken, die größer als unsere größte Ziffer (1) ist, würden wir auch so verfahren wie die Zehnfingerwesen. Also fangen wir wieder bei der kleinsten Ziffer an (die hier auch gleichzeitig die größte und überhaupt die einzige ist), also der 1 und hängen eine Null dran: 10. Wir zählen also jetzt
1, 10, 11, 100, 101, 110, 111, 1000, 1001 und so weiter.
Die Zehnfingerlingzahlen dafür sind: 1, 2, 3, 4, 5, 6, 7, 8, 9 und so weiter.
Die Zweifingerlinge würden also zu meinem guten alten R4 sagen: »Dieser R100 hat 100 Zylinder und 100010 PS«. Leider — oder von der Steuer her Gottseidank — hat sich dadurch aber an der Tatsache nichts geändert, daß er genauso schwach den Berg hinaufklettert wie vorher, nur das Zahlensystem, das ist jetzt Binär. Sehen wir uns das nochmal genauer an. Wissen Sie noch, was in der Mathematik Potenzen sind? Falls nicht, 103sup> heißt 10mal 10mal 10, also die Zehn dreimal mit sich selbst multipliziert. 100sup> ist allerdings 1. Wenn wir nun eine normale Dezimalzahl (eine Zahl der Zehnfingerlinge) vor uns haben, zum Beispiel 255, dann kann man dafür auch schreiben:
255=2*102+3*101+5*100=2*100+5*10+5*1
Rechnen Sie nach: Es stimmt! Genauso ist nun auch eine Binärzahl aufgebaut:
1001=1*23+0*22+0*21+1*20
Deswegen ist es auch relativ einfach, die Zahlen der Zweifingerlinge in unser Zehnfinger-System umzurechnen:
1001=1*23+0*22+0*21+1*20=1*8+0*4+0*2+1*1=9
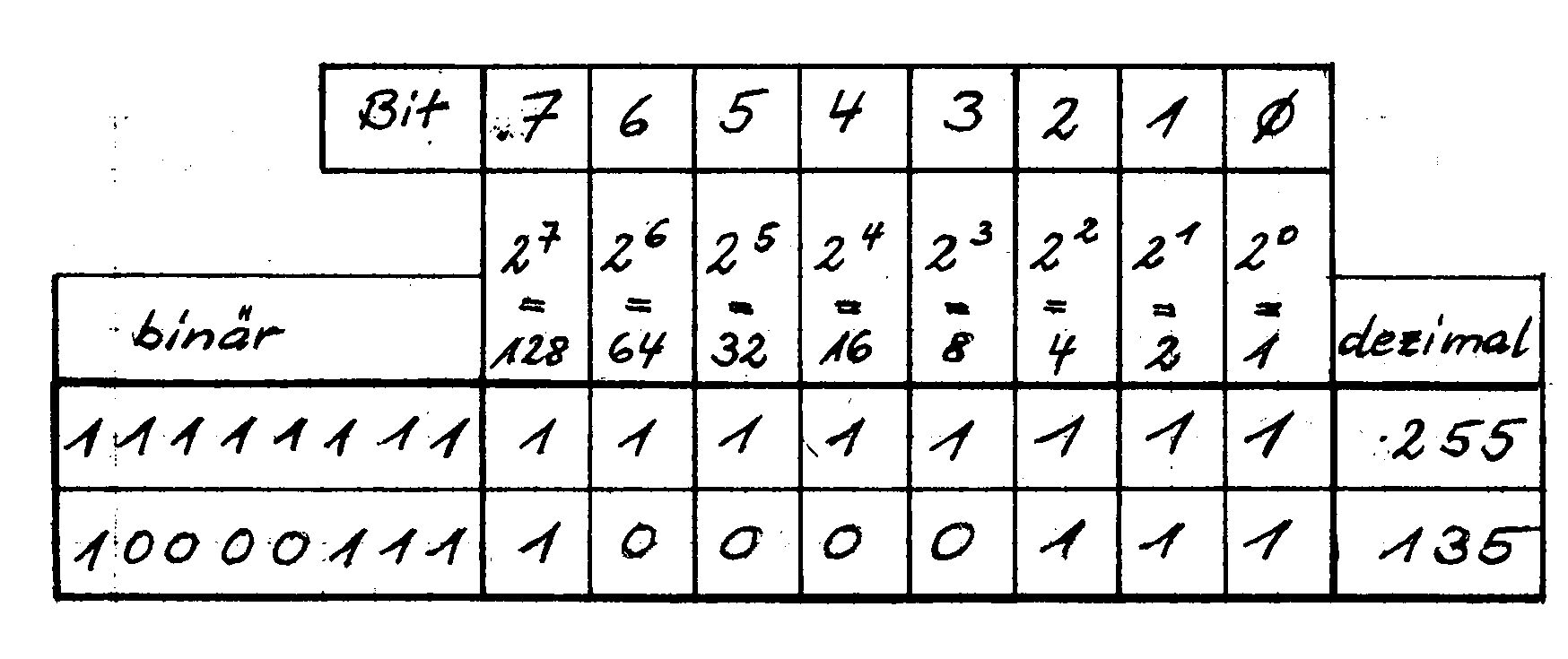
Die bequemste Methode ist es, ein Schema wie in Bild 1 zu benutzen. Andersherum kann man auch ganz einfach unsere Zahlen in die der Zweifingerlinge umrechnen, nämlich wie in Bild 2 gezeigt.
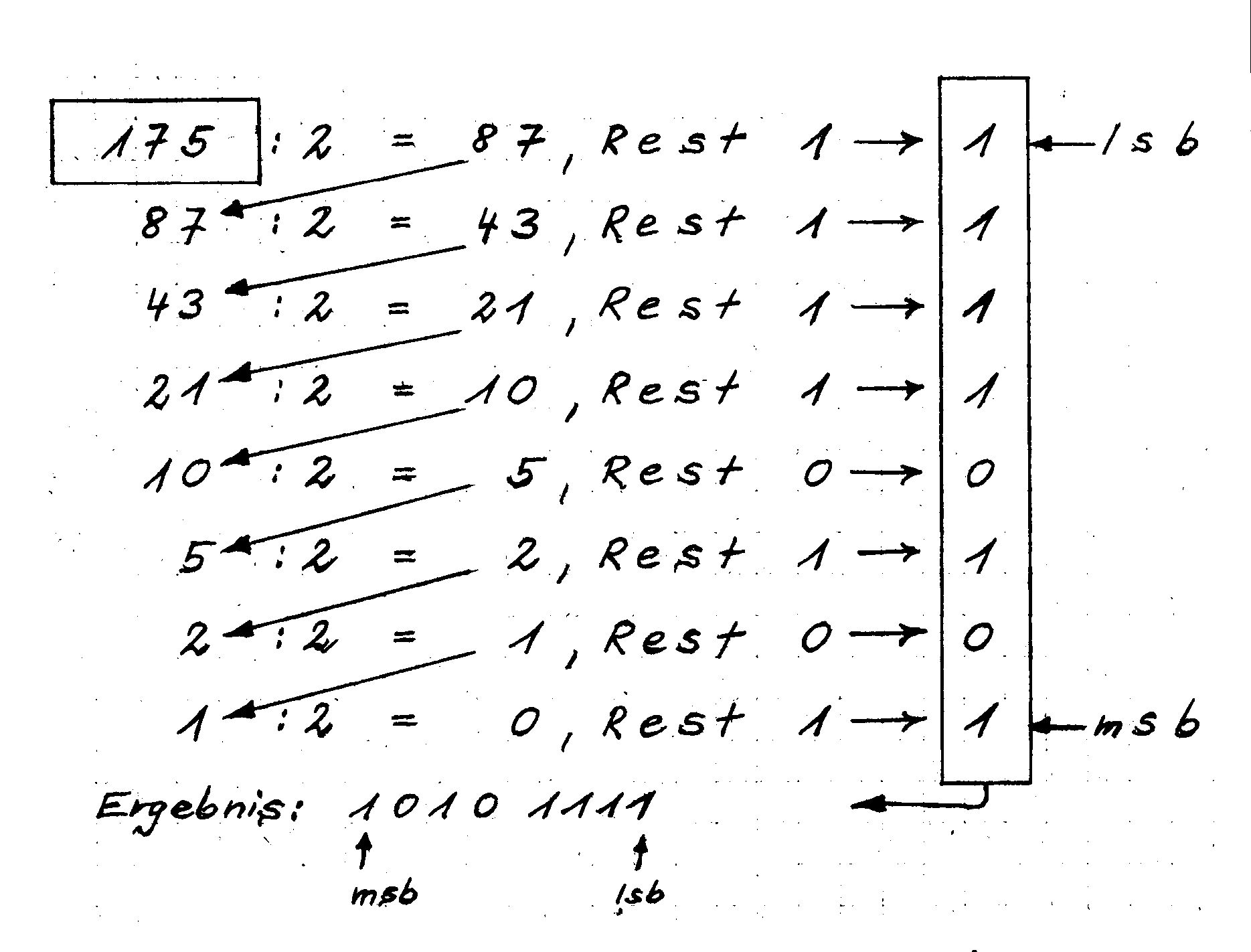
Dabei bedeutet lsb »least significant bit» und msb »most significant bit», also zu deutsch etwa »bedeutsamstes Bit« und »am wenigsten bedeutsames Bit«. Das ist leicht zu verstehen: Es macht keinen so großen Unterschied, ob mir jemand 1001 Mark oder 1002 Mark schenkt. Der Unterschied berührt mich aber schon ganz anders bei 1001 Mark oder 2001 Mark. Für ökonomisch Denkende sei noch bemerkt, daß das Programm SpeiLu (in erweiterter Form hier angefügt) ein schönes Unterprogramm (Zeilen 20000 bis 20030) enthält, welches beliebige Dezimalzahlen in Binärzahlen umrechnet.
Vielleicht haben Sie Lust, zur Übung noch ein bißchen zu rechnen (aber bitte nicht mit dem Unterprogramm):
a) Umrechnung dez→ binär 25,16,47,128
b) Umrechnung binär→ dez 10001,1110,11110000
Die Lösungen finden Sie am Ende dieser Folge.
Wir haben jetzt die Zweifingerlinge ausgiebig kennengelernt und werden mit ihrer Hilfe später einige Hürden nehmen können. Jetzt aber zu den Sechzehnfingerlingen.
Die Entartung der Sechzehnfingerlinge: Das Hexadezimalsystem
Diese Sechzehnfingerlinge begleiten uns auch ständig und zwar als Sechzehnfingerlinge getarnt. Doch bevor wir sie enttarnen, müssen wir etwas mehr über sie wissen. Die Zählweise der Sechzehnfingerlinge mutet uns, die wir nur zehn Finger haben (also auch nur 9 Ziffern und die Null) etwas merkwürdig an, denn was nimmt man — für Ziffern größer als 9 — ohne eine zweistellige Zahl zu benutzen? Wir bemühen das Alphabet:
0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F
Als Zehnfingerlinge würden wir dafür schreiben:
0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
Sobald es um eine Anzahl größer als F (dez. = 15) geht, zum Beispiel F+1, dann kommt auch hier die zweite Stelle dazu: F+1=10 (dezimal wäre das: 15+1=16). Ebenso wie die Dezimalzahlen sind auch die Hexadezimalzahlen auf Potenzen aufgebaut:
$831=8*162+3*161+1*160=8*256+3*16+ 1*1=2097
Dabei steht das Dollarzeichen dafür, daß es sich um eine Hexadezimalzahl handelt, was allgemein üblich ist. Die Umrechnung von Hex-Zahlen in Dezimalzahlen und umgekehrt ist etwas beschwerlicher als die von Binärzahlen. Man behilft sich am besten mit der Tabelle 1. Damit geht die Umrechnung einer Hex-Zahl in eine Dezimalzahl relativ einfach (siehe Bild 3).
| $ | dez. | $ | dez. | $ | dez. | $ | dez. |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 4096 | 1 | 256 | 1 | 16 | 1 | 1 |
| 2 | 8192 | 2 | 512 | 2 | 32 | 2 | 2 |
| 3 | 12288 | 3 | 768 | 3 | 48 | 3 | 3 |
| 4 | 16384 | 4 | 1024 | 4 | 64 | 4 | 4 |
| 5 | 20480 | 5 | 1280 | 5 | 80 | 5 | 5 |
| 6 | 24576 | 6 | 1536 | 6 | 96 | 6 | 6 |
| 7 | 28672 | 7 | 1792 | 7 | 112 | 7 | 7 |
| 8 | 32768 | 8 | 2048 | 8 | 128 | 8 | 8 |
| 9 | 36864 | 9 | 2304 | 9 | 144 | 9 | 9 |
| A | 40960 | A | 2560 | A | 160 | A | 10 |
| B | 45056 | B | 2816 | B | 176 | B | 11 |
| C | 49152 | C | 3072 | C | 192 | C | 12 |
| D | 53248 | D | 3328 | D | 208 | D | 13 |
| E | 57344 | E | 3584 | E | 224 | E | 14 |
| F | 61440 | F | 3840 | F | 240 | F | 15 |
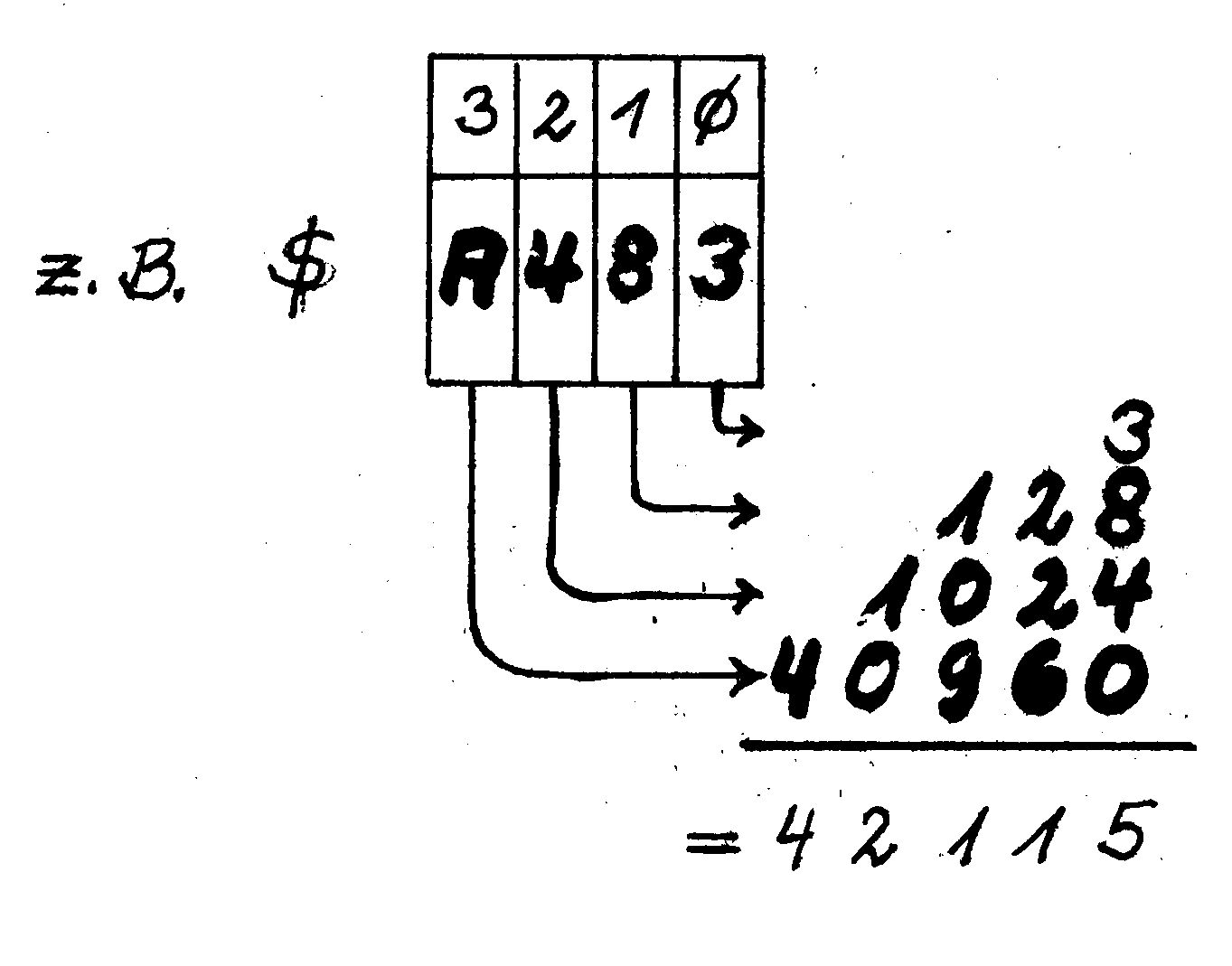
Man sucht sich aus der Tabelle in der Spalte, die dem Stellenwert der Hex-Ziffer entspricht, die dazu gehörige Dezimalzahl. Das führt man für alle Hex-Stellen durch und addiert dann die so gefundenen Dezimalwerte wie im Beispiel gezeigt wird.
Auch die Umwandlung einer Dezimalzahl in die Hex-Zahl ist jetzt nicht mehr so tragisch. Nehmen wir die Dezimalzahl 40959 (siehe Bild 4). Wir suchen aus der Tabelle die größte Dezimalzahl heraus, die gerade noch kleiner als unsere Zahl ist: 36864. Ihr entspricht eine $9 an der 3. Stelle der zu findenden Hexzahl. Wir ziehen dann diese Zahl 36864 von unseren 40959 ab. Es bleiben 4095. Wieder suchen wir jetzt eine Stelle tiefer (also in Spalte 2) die größte Dezimalzahl heraus. Jetzt ist das 3840. Erneut folgt eine Subtraktion und so weiter wie im Beispiel im Bild 4 gezeigt wurde.
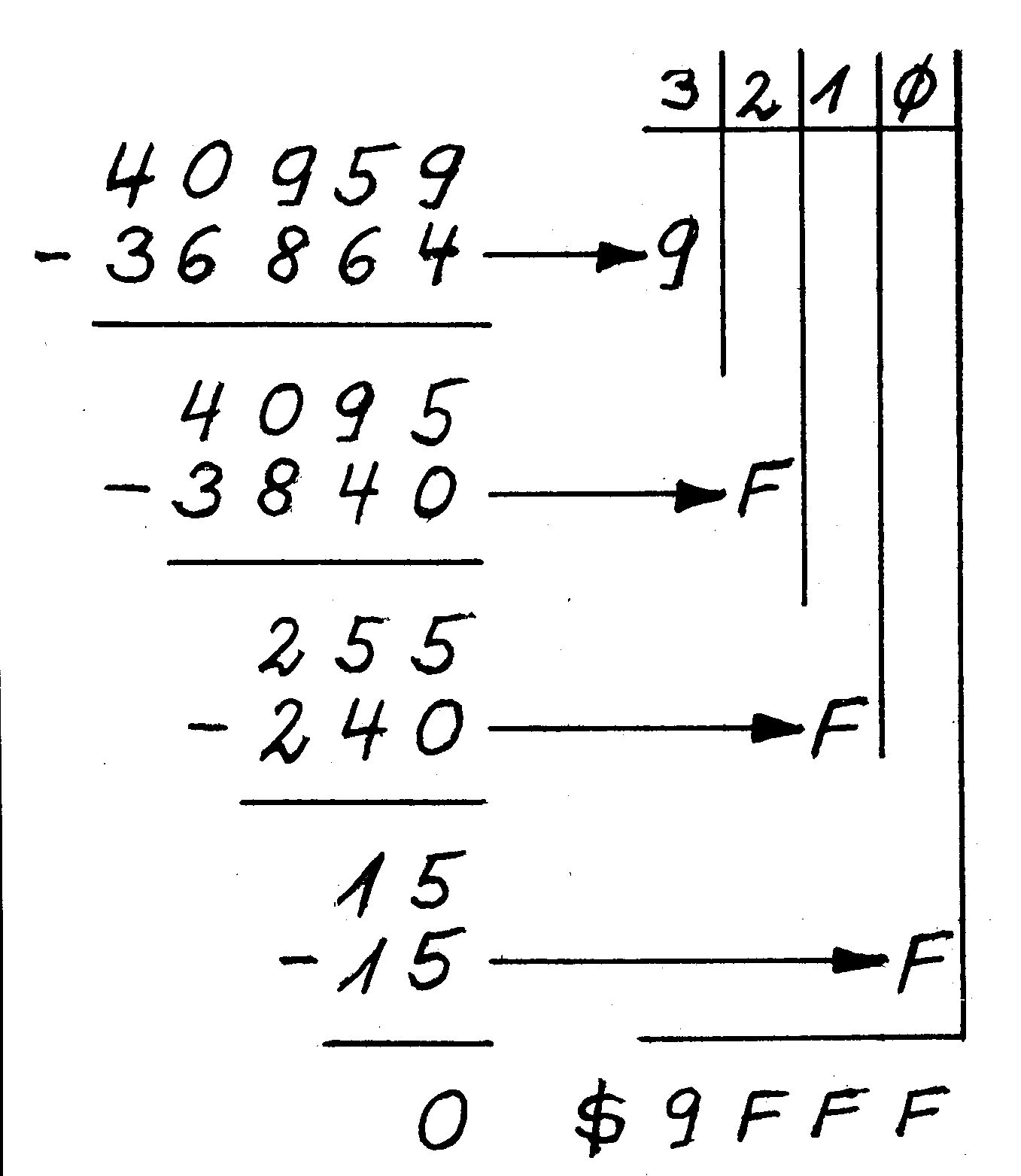
Ich bewundere Ihren Mut, daß Sie mit mir auf dieser Etappe soweit mitgegangen sind. Wir stecken jetzt anscheinend total fest im Dornendickicht. Aber nur noch eine letzte Anstrengung und wir kommen zu einer kleinen Lichtung, auf der wir uns etwas ausruhen können. Dazu werden wir nun die Sechzehnfingerlinge enttarnen.
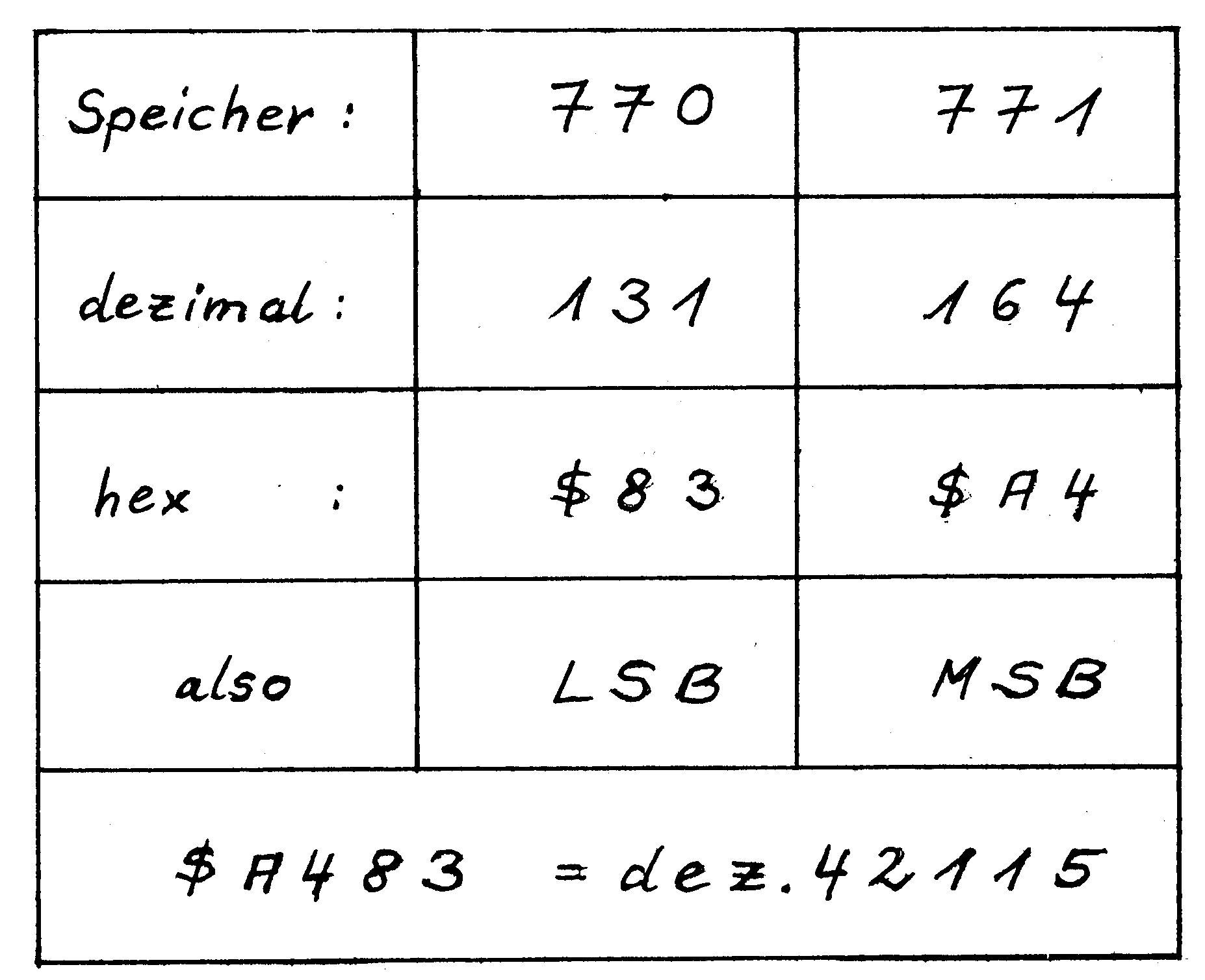
Sehen wir uns dazu die Zahl $FFFF an, die größte mit vier Stellen darstellbare Hex-Zahl. Wenn Sie per Tabelle umrechnen, werden Sie feststellen, daß wir 65535 vor uns haben. Erinnern Sie sich an die Folge 1, wo diese Zahl die Obergrenze unseres gesamten Speichers war? Dann erinnern Sie sich sicherlich auch noch daran, daß in einer Speicher-Hausnummer (Byte) acht Zimmer (Bits) sind, die entweder leer oder voll sein konnten (0 und 1). In Bild 1 ist die Bit-Numerierung zu sehen und wie voll man so eine Hausnummer machen kann. Wie man aber auch dabei erkennt, ist die größte Zahl, die in einem Byte Platz findet 1111 1111 oder dezimal 255 oder — rechnen Sie nach — $FF im Hex-System. Nun kann man sich ja vorstellen, daß zum Beispiel das Betriebssystem häufig im Verlauf der Benutzung irgendwelche Hausnummern angeben muß, zum Beispiel wo eine Routine zu finden ist, ein Text und so weiter. Aber auch das Betriebssystem ist darauf festgelegt, daß in jeder Hausnummer nur 8 Bits vorhanden sind! Wie kann es dann aber zum Beispiel sagen, daß die Basic-Warmstartadressen bei 42115 liegt, wenn es nur bis 255 zählen kann? Ganz einfach: Es gibt sozusagen Wohngemeinschaften, die zwei Hausnummern bewohnen und wenn alle Bits von 2 Bytes voll sind, dann haben wir: 1111 1111 1111 1111 = dezimal 65535. Wenn alle leer sind, haben wir 0. Mit 2-Byte-Adressen kann also der ganze Bereich erfaßt werden. In Bild 3 haben wir berechnet, daß der Adresse 42115 die Hex-Zahl $A483 entspricht. Jetzt zerteilen wir diese Hex-Zahl auf zwei Bytes, von denen das eine MSB (most significant Byte = bedeutsamstes Byte) und das andere LSB (least significant Byte = am wenigsten bedeutsames Byte), genannt wird, wie vorhin msb und lsb bei den Bits.
MSB← →A4 LSB← →83
Beide sind kleiner als $F und können deswegen im Speicher untergebracht werden. Das Betriebssystem notiert sie sich in den Hausnummern 770 und 771 auf page 3. Sehen wir doch einfach mal nach! Geben Sie ein:
PRINT PEEK (770), PEEK (771) »RETURN«
Wir erhalten: 131 164
Lassen Sie sich nicht verwirren! Rechnen wir diese Angaben mal um in Hex-Zahlen (Bild 5). Wir finden also die im Bild 5 dargestellten Werte.
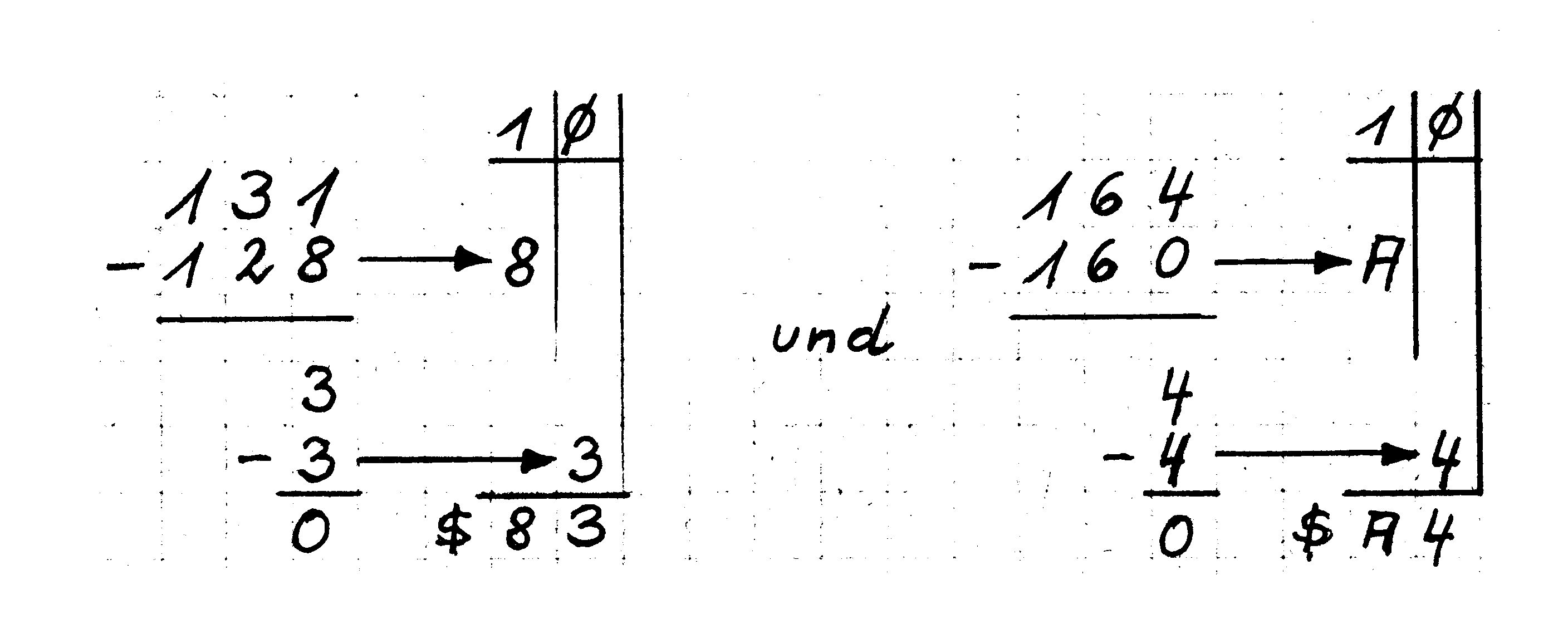
Das sieht alles komplizierter aus als es ist. Mit etwas Übung, die wir uns jetzt zulegen wollen, werden Sie feststellen, daß Sie allerhand damit anfangen können. Die Sechzehnfingerlinge sind also als Dezimalzahlen getarnt gewesen (Bild 6). Auch hier zur Übung einige Aufgaben:
c) Umrechnung hex → dez $92, $D728, $A001
d) Umrechnung dez → hex 65534, 2048, 21235
e) Tun Sie so, als müßten Sie diese letzte Zahl in die Speicherzellen 770 und 771 eingeben. Welche POKEs sind nötig?
So, jetzt wo wir die Hex-Zahlen erkennen können, werden wir uns ihrer kräftig bedienen.
Wir führen den C 64 hinters Licht: Eigene Änderungen an der Speicherorganisation
Jetzt können wir geistig etwas ausspannen. Falls Sie Ihren Computer schon in Betrieb haben, speichern Sie darauf befindliche Programme ab, schalten Sie aus und wieder ein. Wir wollen den Computer im Ursprungszustand etwas untersuchen und dann einige Änderungen vornehmen. Auf der Zeropage gibt es einige nützliche Hausnummern, die wir uns ansehen wollen. Tippen Sie doch mal ein:
PRINT PEEK (43), PEEK (44) »RETURN«
Wir erhalten 1 8
Die Umrechnung mit der Tabelle ergibt $ 801 = dez. 2049. Sehen wir in das Handbuch, Anhang Q auf Seite 160. Dort ist zu lesen, hier sei die Startadresse vom Basic-Text gespeichert. Jetzt machen wir uns das etwas komfortabler. Wir geben im Direktmodus (also ohne Programmzeilennummer) ein:
A = 45:PRINTPEEK(A), PEEK(A + 1), PEEK(A) + PEEK(A + 1)*256 »RETURN«
Wir erhalten: 3 8 2051
Dies ist die Adresse, von der an Variable gespeichert werden. Gleichzeitig erfährt man so, wo ein Basic-Programm aufhört, denn die einfachen Variablen werden direkt hinter dem Basic-Programmtext gespeichert. Jetzt fahren wir den Cursor hoch auf die 45 in der zuletzt eingegebenen Zeile und ändern sie um auf 47, dann »RETURN«. Es erscheint
10 8 2058
Ab 2058 beginnen jetzt die indizierten Variablen. Normalerweise fangen sie im Leerzustand auch bei 2051 an. Wir haben aber eine Variable A definiert und die verschiebt die indizierten Variablen um 7 Bytes. Als Nebeneffekt sehen wir so, daß eine Variable in 7 Bytes gelagert wird. Zur Kontrolle geben wir nochmal ein:
CLR:PRINT PEEK(47), PEEK(48) »RETURN«
und erhalten 3 8 na also!
Diese Untersuchung können Sie noch weiterführen, wenn Sie wollen. Sie erhalten so die Werte in Tabelle 2.
Bevor wir jetzt an die erste Änderung gehen, sehen wir mal nach, wieviel freies Basic-RAM wir zur Verfügung haben:
PRINT FRE(0) + 65536 »RETURN«
Es sollte auch bei Ihnen erscheinen: 38909.
Rechnen Sie entsprechend Bild 7 nach.
Nun wollen wir unserem Computer einreden, sein Basic-Speicher sei schon bei 12288 statt bei 40960 zu Ende. Zunächst müssen wir umrechnen. Wir sehen in die Tabelle 2 und rechnen entsprechend Bild 8 wie gehabt. Also ist das MSB = $30 und das LSB = $00. Jetzt rechnen wir wieder ins Dezimalsystem um:
3*16 = 48 0*16 = 0 0* 1 = 0 und 0* 1 = 0 --------- --------- MSB = 48 LSB = 0
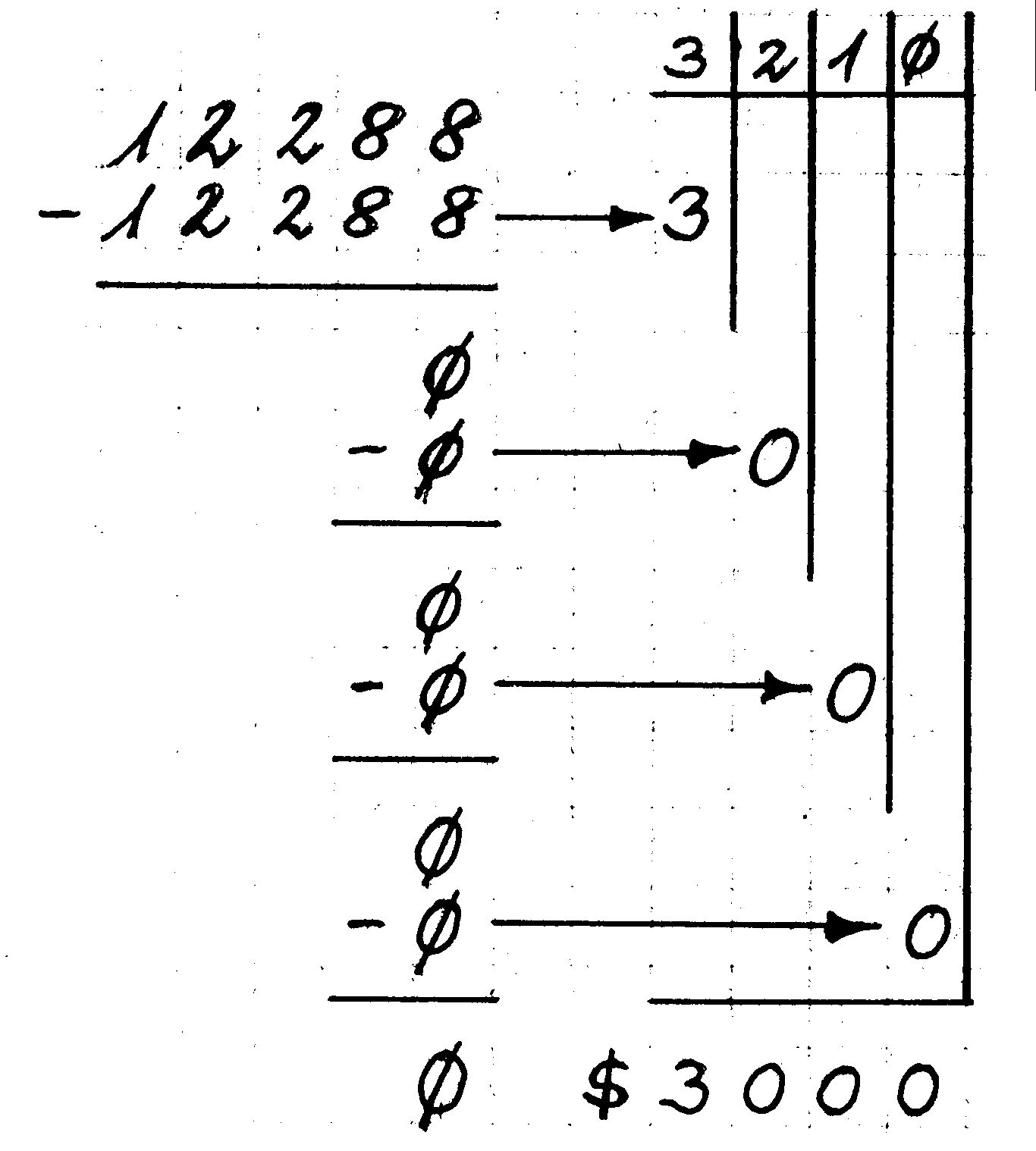
Die höchste Basic-Adresse ist (siehe Tabelle 2) in MEMSIZ gespeichert und deshalb geben wir ein: POKE 55,0:POKE 56, 48 »RETURN« Nun sehen wir nach mit
PRINT FRE(0) und erhalten 10237.
| Adresse | Normaler Inhalt im Leerzustand | |||||
|---|---|---|---|---|---|---|
| Commodore Name (Label) | LSB | MSB | LSB | MSB | Dezimal | Bedeutung |
| TXTTAB | 43 | 44 | 1 | 8 | 2049 | Anfang Basic-Text |
| VARTAB | 45 | 46 | 3 | 8 | 2051 | Variablenstart |
| ARYTAB | 47 | 48 | 3 | 8 | 2051 | Arraystart |
| STREND | 49 | 50 | 3 | 8 | 2051 | Arrayende + 1 |
| FRETOP | 51 | 52 | 0 | 160 | 40960 | Stringstart |
| MEMZIZ | 55 | 56 | 0 | 160 | 40960 | höchste Basic-Adresse |
| MEMSTR | 641 | 642 | 0 | 8 | 2048 | RAM-Start für Betriebssystem |
| MEMSIZ | 643 | 644 | 0 | 160 | 40960 | RAM-Ende für Betriebssystem |
Es ist also geglückt. Der noch freie RAM-Bereich oberhalb von 12288 wird für Basic vom Computer nicht mehr wahrgenommen. Das nennt man »schützen« eines Speicherbereiches vor dem Überschreiben durch Basic. Gleichzeitig sollte man, falls im Basic-Programm auch Strings verwendet werden, auch noch FRETOP berücksichtigen mit:
POKE 51, 0:POKE 52, 48 »RETURN«
Der nun verfügbare Bereich ist in Bild 9 zu erkennen. In SpeiLu wird dieser Schutz in Zeile 10 vollzogen. Jedesmal, wenn man einen Teil des Basic-Speichers für andere Dinge verwenden will als für Basic, muß man diesen Teil in der gezeigten Weise schützen.
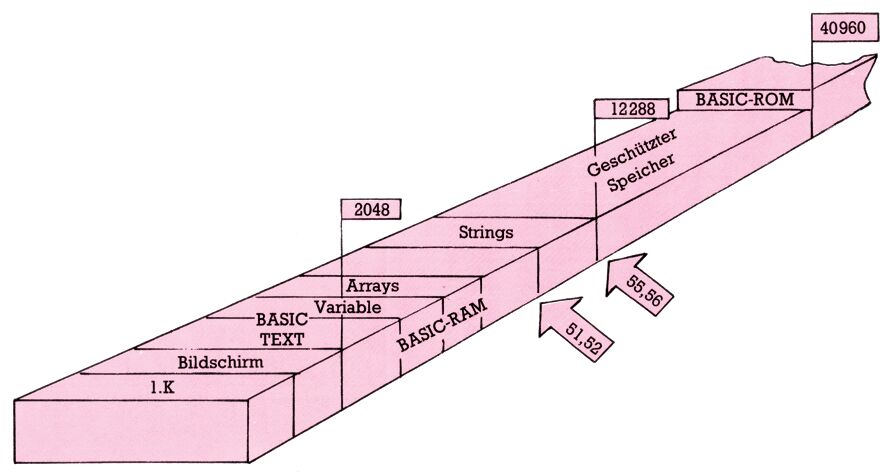
Sie werden vielleicht sagen, daß Sie soooo lange Basic-Programme kaum verwenden und nie in Regionen über 20000 oder 25000 geraten werden. Leider ist das ein Irrtum. Denn die Speicherung von Strings geschieht ab Adresse 40960 abwärts (siehe Bild 7). Ein »sicherer« Bereich im Basic-Speicher (ohne ihn schützen zu müssen) könnte höchstens irgendwo ungewiß mitten drin sein, wo weder von unten das Basic-Programm mit seinen Variablen noch von oben die Strings anstoßen würden. Darauf würde ich mich aber lieber nicht verlassen. Schützen ist besser. Wir werden im Verlauf der weiteren Folgen noch eine Reihe weiterer Möglichkeiten benutzen um die Speicherorganisation umzukrempeln.
Und oder? Oder und? Die Befehle AND, OR
Jetzt haben wir beinahe alles Handwerkszeug beieinander, um unabhängig von irgendwelchen Fertigprogrammen uns selbst neue Zeichen zu definieren und auch zu bestimmen, woher der Computer sie dann holen soll. Nur eine Tatsache stört noch. Wir wissen jetzt zwar, wie wir in unserem C 64 ganze Bytes ändern können indem wir Adressen POKE-fertig umrechnen und dann einPOKEn. Was tun wir aber, wenn — was uns häufig beschäftigen wird — nicht das ganze Byte, sondern nur ein halbes (ein sogenannter Nibble) oder gar nur ein einziges Bit verändert werden soll? Natürlich gibt es dann fast immer die Möglichkeit, durch ein PEEK nachzusehen, was im Byte drin ist, das dann ins Binärsystem umzurechnen, dann die Binärzahl nach unserem Wunsch zu ändern, sie wieder ins Dezimalsystem umzurechnen und dann schließlich einzuPOKEn.
Sehr umständlich! Basic sei Dank gibt es da zwei Befehle, die uns den Aufwand verringern helfen: AND und OR. Es handelt sich um sogenannte logische Operatoren, die zwei Dinge oder Aussagen miteinander verbinden und daraus ein Ergebnis produzieren. Zunächst mal zu AND. Wir kennen das von Basic her zum Beispiel in der IF...THEN..Verzweigung:
5 IF A = 2 AND B = 200 THEN 10
Nur dann, wenn A = 2 und B = 200 ist, erfolgt ein Sprungnach Zeile 10, das heißt, wenn beide miteinander verknüpften Bedingungen erfüllt sind, ist das Ergebnis der Verzweigung erzielt. Bei binären Zahlen ist das einfacher:
1 AND 1 = 1. Wenn also beide Ziffern 1 sind, ist das Ergebnis 1. Man faßt das gerne in einer Tabelle zusammen (Tabelle 3).
| AND | 1 | 0 |
|---|---|---|
| 1 | 1 | 0 |
| 0 | 0 | 0 |
Wie wendet man das an? Nehmen wir an, ein Byte sähe binär so aus: 1111 1011. Wir möchten es verändern, so daß es zu 0000 1011 wird. Dann setzen wir die AND-Operation ein:
1111 1011 unser Byte
0000 1111 eine sogenannte Maske
AND ---------
0000 1111 unser Ergebnis
Das heißt, alle Bits, die mit einer 1 AND-verknüpft worden sind, bleiben unverändert. Alle Bits, die dagegen mit einer 0 AND-verknüpft wurden, sind jetzt 0. Anstelle der ganzen Rechnerei muß also jetzt nur die Maske umgerechnet werden: 0000 1111 = 15 dezimal. Nehmen wir an, unser Byte wäre die Adresse 770, dann sähe die Änderung jetzt so aus:
POKE 770, PEEK (770) AND 15
Halt! Geben Sie das aber nicht wirklich ein, denn damit verändern Sie den Basic-Warmstart-Vektor und den brauchen wir noch. Sollten Sie's schon getan haben, dann erfreuen Sie sich noch ein wenig des Effektes und ziehen Sie dann die Notbremse: Computer aus- und wieder anschalten.
Nun zu OR. Auch das kennen wir vom Basic her, zum Beispiel:
5 IF A = 2 QR B = 200 THEN 10
Wenn also A = 2 ist oder wenn B = 200 ist oder wenn beide Bedingungen erfüllt sind, erfolgt der Sprung nach 10. Ebenso wie für AND kann man auch hier die Verhältnisse am besten mit einer Tabelle übersehen (Tabelle 4).
| OR | 1 | 0 |
|---|---|---|
| 1 | 1 | 1 |
| 0 | 1 | 0 |
Die Anwendung sieht dann so aus (wir nehmen unser Ergebnis von vorhin 0000 1011):
0000 1011
1111 0000 eine Maske
OR ---------
1111 1011 das neue Ergebnis.
Überall dort also, wo mindestens eine 1 steht, ergibt sich im Endausdruck auch eine 1.
Während man mit AND gezielt Bits löschen kann, vermag man mit OR gezielt Bits zu setzen. Beide Operationen können natürlich auch miteinander kombiniert werden. Es gilt die alte Jungprogrammiererregel: Probieren, probieren,...
Ein Beispiel stelle ich Ihnen nochmal genau vor, das wir gleich verwenden werden. Erinnern Sie sich, daß wir in der letzten Folge das Byte 53272 etwas genauer angesehen haben. Die unteren 4 Bits (genau genommen ohne Bit 0) geben an, wo die Punktmuster für die Zeichen abrufbereit stehen. Durch PEEK (53272) fanden wir den Dezimalwert 21. Das entspricht dem Binärwert 0001 0101.
Wobei der eingerahmte Teil also für den Ort der Zeichen zuständig ist. In der Tabelle 5 sehen Sie, welche Kombinationen auf welche Speicherorte als Startadressen unserer Zeichenmuster deuten.
| Zahlenwert | Bitmuster des Bits 0-3 | Startadresse Zeichenspeicher | ||
|---|---|---|---|---|
| (Bit 0 = 0) | Byte 5372 | dez. | hex | |
| 0 | XXXX000X | 0 | $0000 | |
| 2 | XXXX001X | 2048 | $0800 | |
| 4 | XXXX010X | 4096 | $1000 | Einschaltzustand |
| 6 | XXXX011X | 6144 | $1800 | |
| 8 | XXXX100X | 8192 | $2000 | |
| 10 | XXXX101X | 10240 | $2800 | |
| 12 | XXXX110X | 12288 | $3000 | |
| 14 | XXXX111X | 14336 | $3800 | |
Wenn wir nun also einen anderen Ort eingeben wollen, dürfen wir nur die Bits 1 bis 3 verändern. Lassen Sie uns die Zeichen nicht mehr von 4096 an, sondern von 6144 an gespeichert haben! Zunächst einmal müssen die Bits 4 bis 7 vor jeder Änderung geschützt sein und die Bits 0 bis 3 gelöscht werden:
dez. 21 0001 0101 das ist unser PEEK (53272) dez. 240 1111 0000 eine Maske, die AND-verknüpft wird dez. 16 0001 0000 das ist: PEEK (53272) AND 240
Jetzt können wir gezielt Bits setzen. Wir brauchen die Kombination 011X. Wenn wir für X einfach 0 annehmen (das geht, weil Bit 0 hier nicht beachtet wird) dann ergibt das einen Dezimalwert von 6 (siehe Tabelle 5).
dez. 16 0001 0000 unser Zwischenwert dez. 6 0000 0110 Maske wird OR verknüpft dez. 22 0001 0110 unser Endwert
Alles in allem geben wir ein:
POKE 53272, (PEEK (53272) AND 240) OR 6
Das können Sie gefahrlos eingeben und sich am Ergebnis freuen. Wenn Sie danach übrigens mal mit PEEK (53272) abfragen, werden Sie nicht 22, sondern 23 erhalten, was an Bit 0 liegt, das wir so nicht beeinflussen können.
Frankensteins freundliches Monster: Eigene Zeichen
Wieso kann man eigentlich eigene Zeichen definieren, wo es sich doch um ein Zeichen-ROM handelt, woraus der C 64 seine Zeichen bezieht? Zum Umbauen der Zeichen muß man doch in die Punktmatrix hineinschreiben und das geht nur ins RAM. Na, dann kopieren wir doch einfach das Zeichen-ROM in den RAM-Bereich. Dort können wir dann nach Herzenslust herumPOKEn. Dazu muß man allerdings wissen, daß drei Dinge zu beachten sind:
a) Sobald wir dem Computer gesagt haben, wo er seine Zeichen herholen soll, kennt er alle die Zeichen nicht mehr, die nicht mit kopiert worden sind. Man muß sich also vorher überlegen, welche Zeichen man braucht und erst dann kopieren (siehe dazu in Folge 1 die Tabelle 2).
b) In Folge 1 ist erwähnt worden, daß der Computer gebaut ist, daß er ständige Wechsel durchführt zwischen den Etagen unseres Speichers. Außerdem verrichtet er noch eine Reihe anderer Tätigkeiten nach einem schnell vor sich gehenden System von lauter Unterbrechungen. Beim Kopiervorgang sollte keine Unterbrechung stattfinden, weil sich der Computer solange auf das Zeichen-ROM konzentrieren soll. Man muß also das sogenannte Interrupt-System während des Kopierens abschalten.
c) Wir kopieren unsere Zeichen ins RAM, müssen den dafür verwendeten Speicherraum also vor dem Überschreiben durch ein Basic-Programm schützen.
Es empfiehlt sich folgende Vorgehensweise:
A. Schützen des RAMs. Dazu wollen wir den Bereich verwenden, der auch in SpeiLu eine Rolle spielt
10 POKE 52, 48: POKE 56, 48
Für das folgende sollten Sie sich das Unterprogramm ab Zeile 40000 von SpeiLu ansehen.
B. Abschalten des Interrupt. Das macht einen Besuch beim CIA# 1, Hausnummer 56 334 nötig. Mit einer AND-Operation knipsen wir die Unterbrechung ab:
20 POKE 56 334, PEEK (56 334) AND 254
C. Nachdem der Computer nicht mehr per Interrupt die Etagen abläuft, muß er behutsam zum Zeichen-ROM geführt werden:
30 POKE 1, PEEK (1) AND 251
Behutsam deswegen, weil wir Byte 1 aus der ersten Folge noch in unguter Erinnerung haben. Wir werden es später besser kennenlernen.
D. Nun steht dem Kopieren nichts mehr im Wege. Wir kopieren alles:
40 FOR I = 0 TO 4 095:POKE 12 288 + I, PEEK (53248 + I): NEXT
Das dauert allerdings eine Weile.
E. Nun muß das Interrupt-System wieder in den Ausgangszustand zurückversetzt werden:
50 POKE 1, PEEK(1)OR 4
60 POKE 56 334, PEEK(56 334)OR 1
F. Jetzt teilen wir dem Computer mit, daß er in Zukunft seine Zeichen ab 12 288 und nicht mehr im Zeichen-ROM findet:
70 POKE 53 272, (PEEK(53 272) AND 240) OR 12
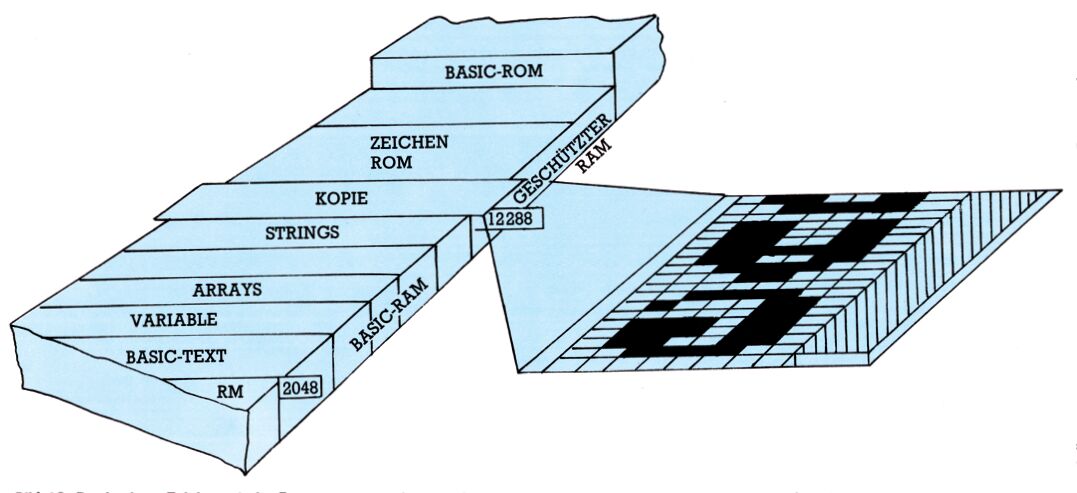
Nach dem RUN merken Sie — wenn alles richtig war — noch keinen Unterschied, außer, daß wir uns eine Menge Speicherplatz weggeschnitten haben. Aber nun wollen wir ans Zeichenumbauen gehen. Nehmen wir mal an, daß wir den Buchstaben A zu langweilig finden. Wir werden ihm ein neues Image verleihen. Wenn Sie sich an die Folge 1 erinnern, dann ist der Buchstabe A nach dem Klammeraffen@ der zweite Buchstabe. Sein erstes Byte ist an achter Stelle des Zeichen-ROMs, also ab 53 256, zu finden. Nachdem wir jetzt kopiert haben, finden wir ihn ab 12296 (siehe Bild 10), und jetzt verstehen wir auch das Bild 8 in Folge 1 als gesetzte und gelöschte Bits anzusehen (Bild 11).
| Byte | binär | dezimal |
| 12296 | 00011000 | 24 |
| 12297 | 00111100 | 60 |
| 12298 | 01100110 | 102 |
| 12299 | 01111110 | 126 |
| 12300 | 01100110 | 102 |
| 12301 | 01100110 | 102 |
| 12302 | 01100110 | 102 |
| 12303 | 00000000 | 0 |
Wir zeichnen uns ein 8 x 8-Raster und konstruieren darin unser neues »A« (Bild 12).
| Byte | binär | dezimal |
| 12296 | 01100110 | 102 |
| 12297 | 00000000 | 0 |
| 12298 | 00011000 | 24 |
| 12299 | 00011000 | 24 |
| 12300 | 10000001 | 129 |
| 12301 | 01100110 | 102 |
| 12302 | 00111100 | 60 |
| 12303 | 00000000 | 0 |
Dann berechnen wir die Dezimalwerte der Bytes und geben schließlich ein:
80 POKE12296, 102:POKE12297,0: POKE12298, 24:POKE12299,24: POKE12300, 129
90 POKE12301, 102:POKE12302,60: POKE12303, 0
Wenn Sie dieses Porgramm mit RUN starten, dann lächelt Sie künftig das A freundlicher an als bisher. Natürlich läßt sich das alles auch viel eleganter lösen. Besonders die Zeilen 80 und 90 können durch eine kleine Schleife, die DATA-Zeilen liest und in den Speicher POKEd, ersetzt werden. Die Adressen können durch Multiplikation des Commodore-Codes mit 8 berechnet werden:
Startadresse des Zeichens mit Code C=12288+8*C
Außerdem finden Sie im Anschluß das erweiterte Programm SpeiLu, das es auf einfache Weise gestattet, Zeichen zu ändern. Nach dem Ändern der Zeichen kann auch der normale Zeichensatz wieder benutzt werden — wenn nötig — durch Eingabe des ursprünglichen Wertes 21 in Hausnummer 53272. Falls Sie SpeiLu benutzt haben, gibt es zwei Möglichkeiten, den alten Zustand wieder herzustellen:
1) Computer aus- und wieder anschalten oder
2) POKE 53272, 21:POKE52,160: POKE56, 160 (Warum, das wissen Sie ja jetzt aus dieser Folge)
Schließlich noch eine Bemerkung: Obwohl manche Basic-Befehle nach der Änderung etwas vergnügter aussehen als vorher, funktioniert zum Beispiel T?B(5) genausogut wie TAB(5). Testen Sie mal: TAB(10)"ABRAKADABRA".
Wenn Sie auf Kleinschreibung oder REVERSE umschalten, sieht alles wieder normal aus.
Damit sei’s für heute genug. Es war eine schwere Etappe. Sie haben sich tapfer durch das Dornengestrüpp geschlagen! Sie werden es nicht bemerkt haben aber wir sind Dornröschen schon ziemlich nahe gekommen. Bis zum nächsten Aufbruch können Sie sich die Zeit damit vertreiben, einen eigenen Zeichensatz herzustellen.
(Heimo Ponnath)140 print:print" (3) aendern eines zeichens" 145 print:print" (4) programm-ende" 170 a=val(a$):ifa<0ora>4then160 180 onagosub1000,2000,3000,4000 3000 printchr$(147);chr$(18);tab(1);"aendern von zeichen" 3010 print:print" es koennen zeichen geaendert werden" 3020 print"indem der 'bildschirm-code' des zeichens"; 3030 print" eingegeben wird. ( 0 - 511)":ifts=0thengosub40000 3035 print:print" aendern sie die binaerzahl mit" 3037 print"'0' oder '1' entsprechend. dann <return>" 3040 print:input"code : ";a:ifa<0ora>511thenreturn 3050 printchr$(147):forad=12288+8*ato1228+8*a+7 3060 de=peek(ad):gosub10000:gosub20000:gosub30000:nextad 3070 printchr$(19):ad=ad-9 3080 forq=1to8:printtab(19);:inputa$:ad=ad+1:gosub50000:gosub10000:gosub20000 3090 printchr$(145);" " 3100 printchr$(145);chr$(145):gosub30000:pokead,de:nextq 3110 geta$:ifa$=""then3110 3120 return 4000 end 50000 de=0:fori=1to8:ifmid$(a$,i,1)="1"thende=de+2^(8-i): 50010 nexti:return
Hier noch die Lösungen der Aufgaben:
a) 11001, 10000, 101111, 10000000
b) 17, 14, 240
c) 146, 55080, 40961
d) $FFFE, $800, $52F3
e) POKE 770, 243:POKE 771, 82
