Kudiplo 64
Mit »Kudiplo« lassen sich problemlos mathematische Kurven grafisch darstellen. Egal, ob auf Bildschirm, Plotter oder Matrixdrucker. Gleichzeitig kann man sich vom Computer die Kurvendiskussion geben lassen.
Vielleicht werden Sie fragen, wozu denn die Untersuchung von Funktionen überhaupt nützlich sein kann. Nun, derartige Untersuchungen haben zunächst einen theoretischen Nutzen, weil sie mathematische Zusammenhänge so schön verdeutlichen. Und darum sind sie auch unverzichtbarer Bestandteil des schulischen Mathematikunterrichtes.
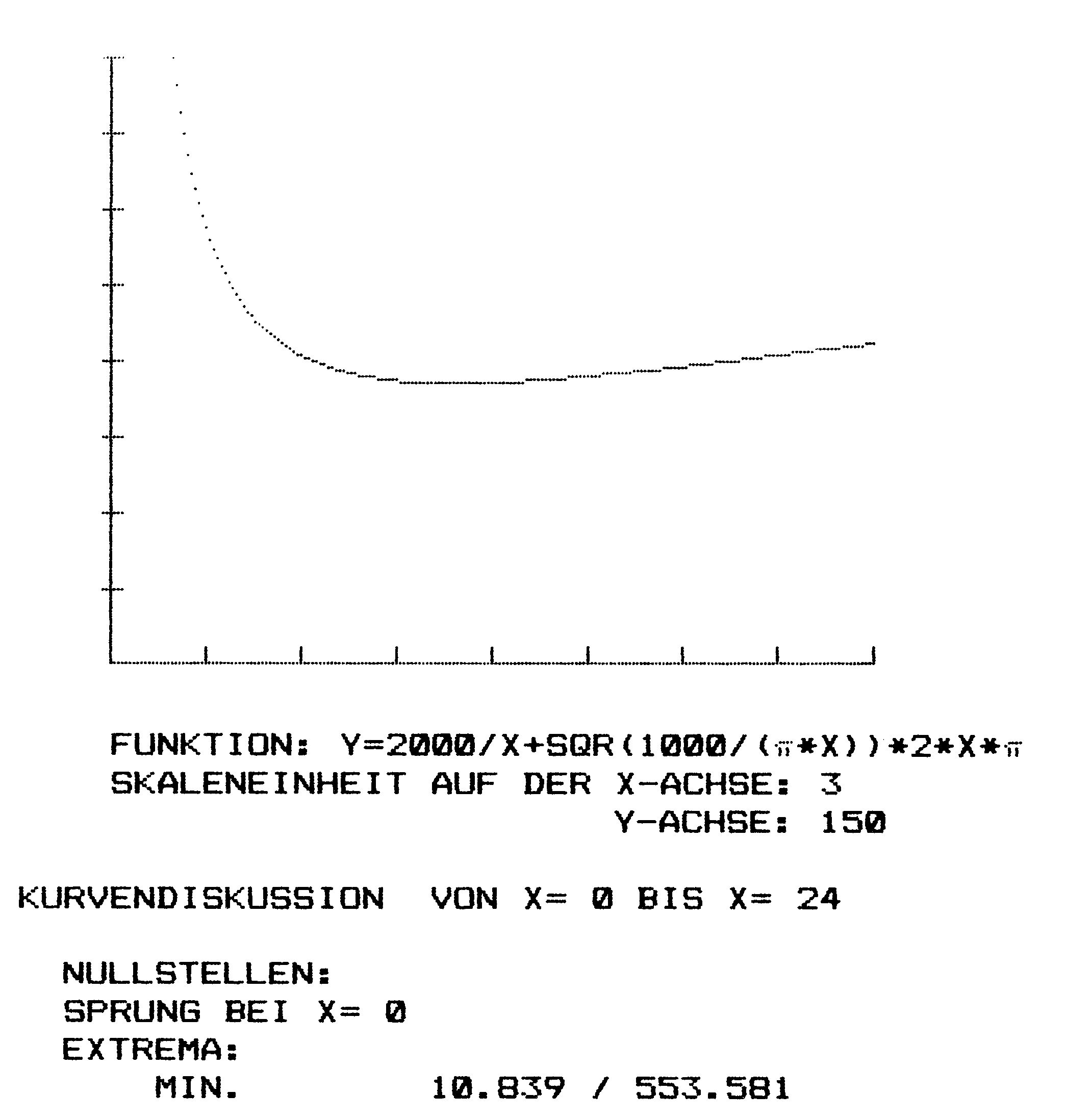
Außerdem gibt es durchaus auch Anwendungen mit unmittelbar praktischem Nutzen. Stellen Sie sich beispielsweise vor, Sie sollten eine Konservendose entwickeln, die bei zylindrischer Form und bei einem Volumen von 1000 cm3 mit möglichst wenig Material hergestellt werden kann, also eine möglichst kleine Oberfläche hat. Ein solches Problem läßt sich durch rechnerisches Probieren nur sehr mühsam lösen. Mit »Kudiplo 64« dagegen, ist die Sache ganz einfach. Aus den Formeln für das Volumen des Zylinders (V= r*r*pi*h) und für die Oberfläche (F=2*(pi*r*r + r*pi*h)) folgt für ein Volumen von 1000 cm3 ein bestimmter Zusammenhang zwischen Zylinderoberfläche und Höhe. Dieser Zusammenhang läßt sich grafisch mit »Kudiplo 64« darstellen (Bild 1, Seite 57) wobei die Höhe des Zylinders auf der waagrechten X-Achse und die in Abhängigkeit hiervon sich ergebende Oberfläche auf der senkrechten Y-Achse eingetragen ist. Am Verlauf der Kurve erkennt man ein Minimum im Bereich der X-Werte 9 und 11. Die Kurvendiskussion ermittelt die Lage des Minimums exakt beim X-Wert 10,839. Wenn Sie jetzt eine Konservendose aus dem heimischen Vorratsschrank überprüfen, werden Sie bei einer l-Liter-Dose ein Höhenmaß von recht genau 10,8 cm feststellen.
Für derart nützliche Untersuchungen stellt »Kudiplo 64« zwei Verfahren zur Verfügung. Nämlich die zeichnerische Darstellung des Kurvenverlaufes einerseits, und die Kurvendiskussion andererseits. Der Benutzer kann dabei wählen, ob die Ausgabe nur auf dem Bildschirm oder auf einem Plotter oder aber per Hardcopy auch auf einem Matrix-Drucker erfolgen soll. Auf diese Weise kann das Programm bei jeder Ausbaustufe des heimischen Rechengenies genutzt werden.
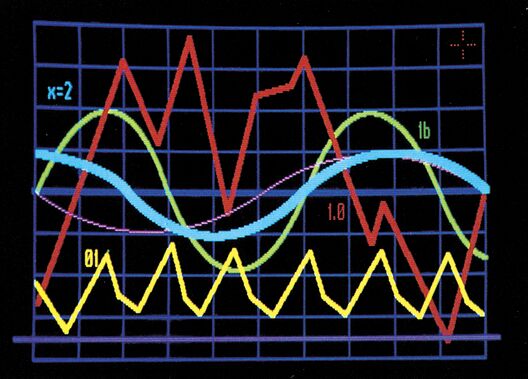
(J. Curdt/og)Das universelle Programm für komfortable Kurvendiskussionen. »Kudiplo 64« erstellt mit geringstem Aufwand auch die entsprechenden Graphen, selbst an kritischen Stellen.
Die eigentliche Stärke eines Computers liegt im Rechnen. »Kudiplo 64« nutzt diese optimal. Im Gegensatz zu anderen Programmen steigt es nicht aus, wenn Definitionslücken auftreten. Da aber eine einfache Funktion wie zum Beispiel y=1/x bei x=0 kritisch wird, kann diese gerade im interessantesten Bereich mit kaum einem Programm untersucht oder gezeichnet werden. »Kudiplo 64« ermöglicht dies durch eine Routine zur Fehlerbehandlung, die in einen vor Basic geschützten Bereich geschrieben wird. Vor möglicherweise fehlerträchtigen Berechnungen wird diese Routine mit GOSUB 2340 ein- und danach mit GOSUB 2350 wieder ausgeschaltet.
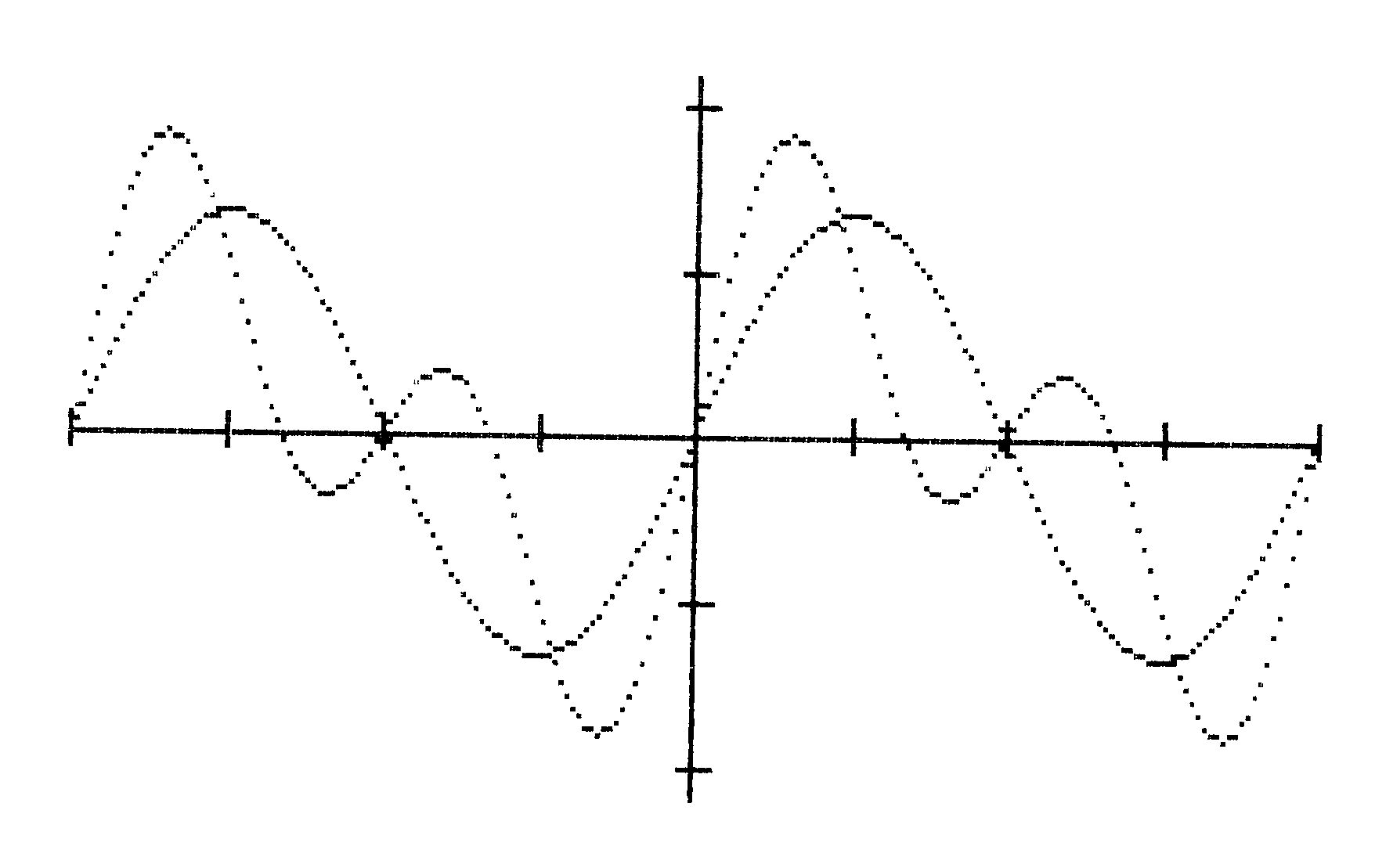
Besonders hilfreich bei der Untersuchung von Funktionen ist auch die Möglichkeit, die Parameter der Darstellung frei wählen zu können. Für die Ausdehnung der X- und der Y-Achse können dabei unterschiedliche Maßstäbe gewählt werden. So wird es möglich, sich zunächst durch die Wahl eines großen Darstellungsbereiches einen groben Überblick über den Kurvenverlauf zu verschaffen und danach die interessantesten Bereiche sozusagen herauszuvergrößern (Bild 2). Zusätzlich kann die Darstellung in Richtung nur einer Achse vergrößert werden. Automatisch wird dabei vom Programm die Lage der Achsen so errechnet, daß ihr Schnittpunkt — sofern möglich — im Nullpunkt liegt. Liegt der Nullpunkt einer Achse außerhalb des dargestellten Bereiches, so wird die Achse an den Rand gezeichnet. Die dazu erforderlichen Berechnungen werden gleich bei der Parameter-Eingabe durchgeführt (ab Zeile 640). Dabei werden nicht plausible Eingaben ignoriert. Solange die Lage des Achsenkreuzes nicht durch Eingabe neuer Parameter verändert worden ist, können in eine Funktionsdarstellung beliebig viele weitere Funktionen eingezeichnet werden (Bild 3). Man kann also beispielsweise eine Funktion durch die Vergrößerung oder Verkleinerung eines Faktors variieren und dann die daraus resultierenden Veränderungen im Kurvenverlauf im Vergleich zwischen mehreren Kurven feststellen.
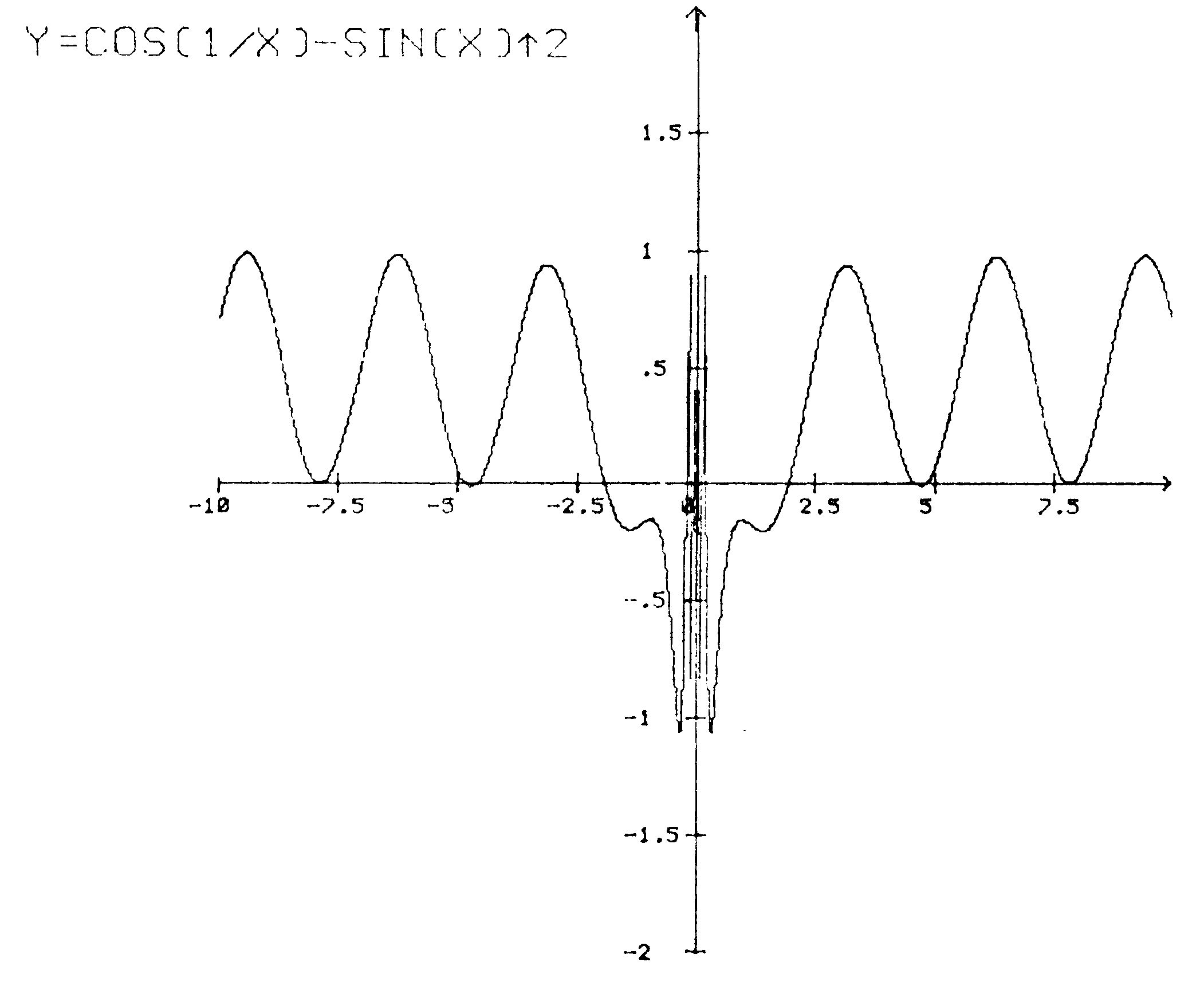
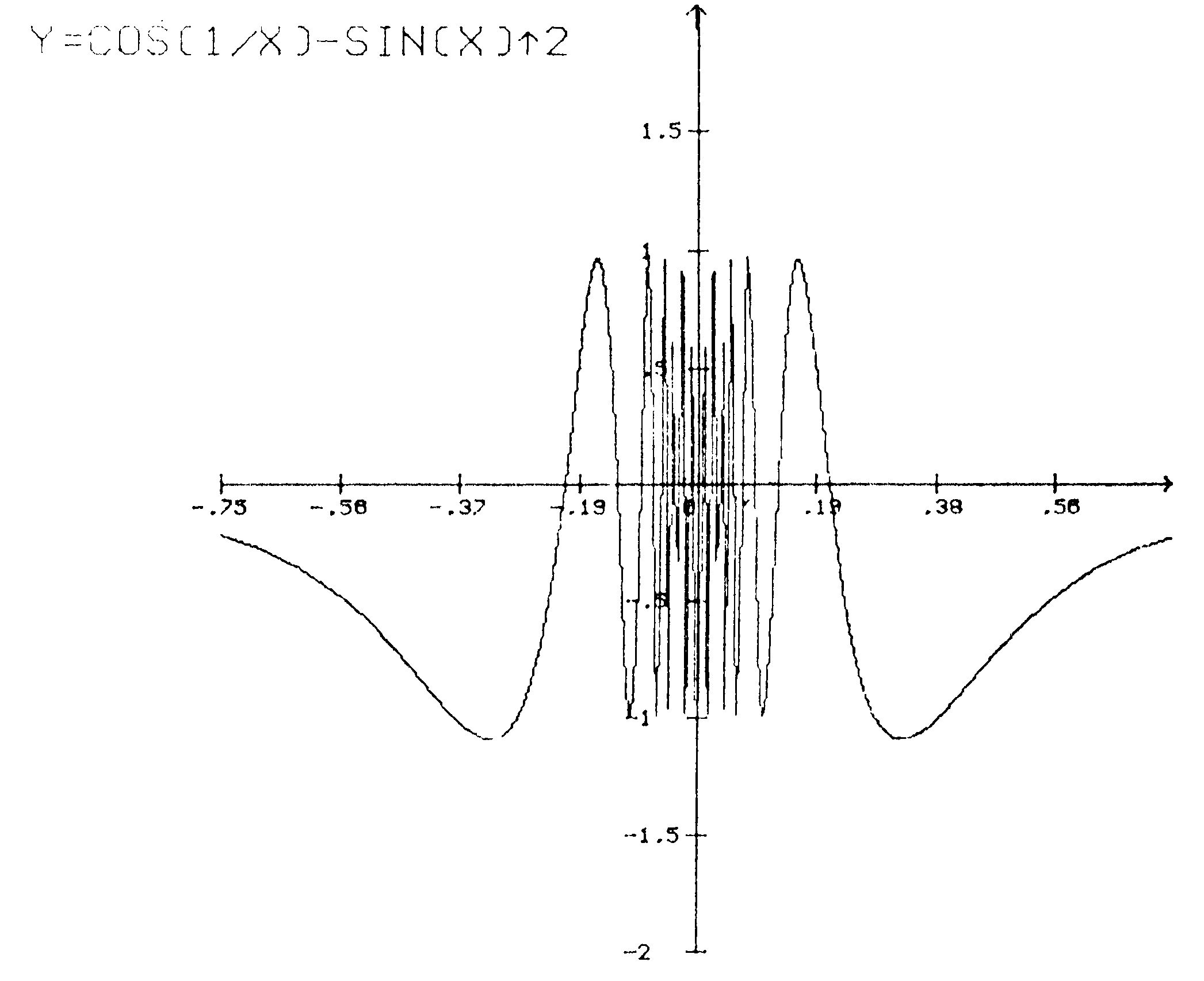
Mathematischen Komfort bietet auch die von »Kudiplo 64« zur Verfügung gestellte Kurvendiskussion. Sie wird jeweils für den gewählten Darstellungsbereich auf der X-Achse ausgegeben und gibt für diesen Bereich zunächst alle Nullstellen an und auch die an der Nullstelle vorhandene Steigung (F'). Zugleich wird die Lage von Sprüngen ermittelt. In einem weiteren Rechengang gibt der Computer die Extremwerte der Funktion mit ihren X/Y-Koordinaten aus, also die Minima, Maxima und Sättel. Fehler können in diesen Routinen dadurch auftreten, daß wegen des gewählten Maßstabs der Darstellung die Kurvensteigung extrem gering ist und darum vom Programm nicht erkannt wird, weil im Interesse größerer Rechengeschwindigkeit nicht mit der vollen Genauigkeit gerechnet wird.
Das Programmlisting ist mit REM-Anmerkungen kommentiert und darum wohl auch ohne ausführliche Beschreibung des Programmlaufes nachvollziehbar. Zu den Zeilen 240, 250, 280 und 290 sowie den Zeilen 1390 und 2260 ist allerdings darauf hinzuweisen, daß der Inhalt dieser Zeilen vom Programm selbst bei Eingabe einer neuen Funktion verändert wird (das bewirkt die Routine in den Zeilen 530 bis 600 mit der bekannten Tastaturpuffer-Methode).
Die genannten Zeilennummern dürfen darum beim Abtippen nicht verändert werden!
Nun zum Abtippen: Beginnen Sie bitte mit dem kleinen Ladeprogramm (Listing 1) und speichern Sie es auf Diskette oder Kassette ab. Es ist erforderlich, um im Basic-Speicher Platz für die Bit-Map freizuhalten. Dazu wird der Zeiger für den Basic-Start hochgelegt auf $4204. Außerdem lädt und startet das Ladeprogramm das Hauptprogramm automatisch nach. Damit das auch bei Benutzung der Datasette funktioniert, muß gegebenenfalls in Zeile 60 die »8« durch eine »1« ersetzt werden.
Anschließend kann das Hauptprogramm (Listing 2) abgetippt werden. Aber bitte nicht starten, sondern zuerst speichern, sonst wird Ihre Fleißarbeit womöglich blitzschnell von der Grafik überschrieben. Sollten Ihnen trotz Checksummer Bedenken kommen, ob Sie die DATA-Zeilen richtig übernommen haben, so erhalten Sie die Prüfsumme, indem Sie provisorisch eingeben: »10 READ A: S=S+A: GOTO 10«. Wenn Sie das Programm nun starten, wird es sich nach kurzer Zeit mit der Fehlermeldung OUT OF DATA ERROR IN 10 beschweren. Im Direktmodus geben Sie nun ein: »PRINT S ⟨RETURN⟩«. Nun müßte als Prüfsumme der Wert 32709 ausgegeben werden. Danach können Sie die Zeile 10 wieder löschen.
In der abgedruckten Form enthält das Programm noch nicht die Hardcopy-Routine für die Arbeit mit einem Matrix-Drucker. Wenn Sie einen solchen Drucker als Ausgabegerät vorsehen wollen, dann müssen Sie das Programm insoweit an Ihre Hardware anpassen. Am besten und präzisesten arbeitet das Programm allerdings zusammen mit dem Plotter 1520. Wenn Sie nur dieses Gerät für die Ausgabe benutzen oder wenn Sie auf eine Hardcopy-Ausgabe verzichten wollen, dann müssen Sie die Zeile 395 weglassen und Sie können dann auch auf die Zeilen 1000, 1120 und 2500 bis 2640 verzichten.
Wenn Sie hingegen den Grafik-Bildschirm als Hardcopy auf einem Matrixdrucker ausgeben wollen, ist folgendes zu beachten: Nachdem in letzter Zeit in der 64’er Maschinenprogramme zur Ausgabe von Hardcopies auf allen gängigen Druckern veröffentlicht worden sind, haben auch Sie möglicherweise bereits ein Programm, mit dem es möglich ist, eine HiRes-Grafik auf Ihrem Drucker auszugeben. Wichtig bei der Auswahl des zu benutzenden Hardcopy-Programmes ist, daß es nicht im Speicherbereich von $C000 bis $C11F (49152 bis 49439) liegt. Dieser Bereich ist bereits von dem Maschinenprogramm zum Erstellen der Bildschirmgrafik und Fehlerroutine belegt.
Für den Fall, daß Ihnen eine solche Hardcopy-Routine nicht zur Verfügung steht, können Sie eines der abgedruckten Hardcopy-Module (Listings 3 bis 5) mit dem MSE abtippen und auf Ihrer »Kudiplo«-Diskette oder auf Kassette speichern. Auf Kassette bitte so, daß das Modul gleich hinter dem Hauptprogramm folgt. Welches Modul Sie auswählen, richtet sich nach dem bei Ihnen verfügbaren Drucker. Das Epson-Modul ist eingerichtet für Epson-Drucker und kompatible Drucker, die über eine Centronics-Schnittstelle mit Geräteadresse 4 betrieben werden.
Hardcopy für alle Drucker
Den Namen des von Ihnen gewählten Hardcopy-Moduls fügen Sie bitte in der Zeile 395 ein, damit diese Routine vom Hauptprogramm nachgeladen wird. Zusätzlich muß in Zeile 2540 der Befehl für den Einsprung in die Hardcopy-Routine eingefügt werden. Im abgedruckten Listing des Hauptprogramms sind diese beiden Zeilen auf das Modul »HC Epson 49440« zugeschnitten. Wenn Sie dieses Modul verwenden wollen, können Sie diese Zeilen unverändert übernehmen.
Sollte das Modul »HC Epson 49440« bei Ihnen nicht funktionieren, so könnte es an dem von Ihnen verwendeten Interface liegen. In diesem Fall haben Sie die Möglichkeit, sich das benötigte Hardcopy-Modul nach Ihren Bedürfnissen selbst herzustellen. Dazu benötigen Sie das in dieser Zeitschrift, Ausgabe 8/1984, Seite 83 abgedruckte Programm von Frank Lonczewski. Zu beachten ist dann nur noch, daß für die Zusammenarbeit mit »Kudiplo« die Hardcopy-Routine in den Speicherbereich ab 49440 (=$C120) geschrieben werden und daß die Startadresse des Grafikbildschirms mit 8192 (=$2000) angegeben werden muß.
Oder wollen Sie mit einem MPS-Drucker arbeiten? In diesem Fall hilft eins der anderen Module. Als Aufruf des Moduls ist dann für das Modul »MP-802-49440« in Zeile 2540 einzusetzen: »SYS 49440,2,0« und für das Modul »MP 801-49525« der Einsprungsbefehl OPEN4,4: SYS49525,4: Close4.
Nähere Einzelheiten für die Arbeit mit dieser Hardcopy-Routine finden Sie in Ausgabe 10/1984, Seite 82. Je nach der Art des von Ihnen verwendeten Druckers und Interfaces muß möglicherweise auch die Geräteadresse in dem OPEN-Befehl in Zeile 2560 geändert werden.
Nachdem Sie das Hauptprogramm auf Diskette oder Kassette gespeichert haben, kann das Vergnügen beginnen. Das Vorprogramm wird geladen und gestartet. Nach kurzer Zeit meldet sich »Kudiplo 64« mit dem Eingabe-Menü und damit hat Ihr Forsch- und Spielsinn ein neues Betätigungsfeld, auf dem Sie sicher viel Interessantes entdecken werden.
(J. Curdt/og)10 rem ladeprogramm kudiplo
20 rem legt basic start auf $4204=16900
30 co=53280:pokeco,11:pokeco+1,11
40 print"{clr}{gry1}fori=0to2:poke16898+i,0:next{down}{down}"
50 print"poke43,4:poke44,66:new{down}{down}"
60 print"load"chr$(34)"kudiplo 64"chr$(34)",8{down}{down}{down}{down}"
70 print"run"
80 printtab(45)"{blk}kudiplo 64 wird geladen{gry1}"
90 poke631,19:fori=632to636:pokei,13
100 next:poke198,6:end
100 rem***********kudiplo**************
110 rem funktion diskutieren + plotten
120 rem mit c-64 und plotter vc-1520
130 rem
140 rem juergen curdt
150 rem kessemeierweg 5
160 rem 493 detmold
170 rem
180 rem********************************
190 poke53280,11:poke53281,11:af=11
200 :
210 rem parameter und variable lesen
220 :
230 ein=49152:of=49410:an=49234:cl=49182:fb=49203
240 f$="sin(x)+ sin(x*2)"
250 deffnf(x)=sin(x)+ sin(x*2)
260 deffnf1(x)=(fnf(x+1e-4)-fnf(x-1e-4))/2e-4
270 deffnf2(x)=(fnf1(x+1e-4)-fnf1(x-1e-4))/2e-4
280 xu=-4:xo= 4:yu=-4:yo= 4:oy= 0
290 xn= 280:yn= 0
300 xe=(xo-xu)/16:ye=(yo-yu)/16:xw=xu
310 print"{clr}{blk}"tab(81)"funktionen plotten und diskutieren mit"
320 print" c 64 und printer-plotter vc-1520 oder bildschirmausgabe
330 fori=0to39:print"{CBM-O}";:next:print
335 :
340 rem eingabe der funktion
345 :
350 printspc(120)"als funktion wird dargestellt:"
360 x=5:y=15:gosub2370:print"{wht}y=";f$
370 printtab(160):ifpeek(49152)+peek(49153)=62then400
380 printtab(5)"{wht}ein wenig geduld bitte !"
390 gosub5000:syscl
395 load"hc epson*",8,1
400 print"{up}{blk}soll die funktion veraendert werden ?":printtab(57)"j/n"
410 gete$:ife$="n"then590
420 ife$<>"j"then410
430 print"{clr}{blk}"tab(80)"bitte die funktion eingeben oder aendern"
440 fori=0to39:print"{SHIFT-*}";:next:print
450 print"wenn die funktion im divisor den{$a0}faktor x enthaelt, sollte der ganze ";
460 print"divisor in klammern gesetzt werden.":print
470 fori=0to39:print"{CBM-O}";:next:print
480 x=5:y=16:gosub2370:print"{wht}y= "f$;
490 printtab(243)"eingabe in ueblicher basic-syntax
500 x=7:gosub2370:inputf$
510 print"{clr}"tab(240)tab(250)"{blk}moment bitte !"
520 print"{home}{gry1}240f$="chr$(34)f$chr$(34)"
530 print"250deffnf(x)="f$"
540 print"280 xu="xu"{left}:xo="xo"{left}:yu="yu"{left}:yo="yo"{left}:oy="oy
550 print"1390y="f$":goto1410"
560 print"2260y="f$":goto2280"
570 print"290 xn="xn"{left}:yn="yn:print"sv="sv"{left}:bs="bs"{left}:af="af"{left}:goto220{down}{down}"
580 poke631,19:fori=632to640:pokei,13:next:poke198,9:end
590 print"{clr}{blk}"tab(120)"die parameter fuer die darstellung:"
600 printtab(120)"unterster x-wert: {wht}"xu
610 printtab(80)"{blk}oberster x-wert: {wht}"xo
620 printtab(120)"{blk}unterster y-wert: {wht}"yu
630 printtab(80)"{blk}oberster y-wert: {wht}"yo
640 printtab(120)"{blk}sollen die parameter veraendert werden ?":printtab(17)"j/n"
650 gete$:ife$="n"then820
660 ife$<>"j"then650
670 print"{wht}";:syscl:bs=0:sv=0
680 x=16:y=7:gosub2370:inputxu
690 x=16:y=10:gosub2370:inputxo
700 xe=(xo-xu)/16:ifxe<=0then680
710 ifsgn(xu)=sgn(xo)thenxn=80:goto730
720 xn=abs(xu)*25/xe+80
730 x=16:y=14:gosub2370:inputyu
740 x=16:y=17:gosub2370:inputyo
750 ye=(yo-yu)/16:ifye=<0then730
760 rem achsenschnittpunkt berechnen
770 ifsgn(yu)<>sgn(yo)then800
780 ifyo<=0thenyn=200:oy=abs(yo*25/ye)+200:goto810
790 ifyu>=0thenyn=-200:oy=-200-yu*25/ye:goto810
800 yn=abs(yu)*25/ye-200:oy=yn
810 goto590
815 :
820 rem hauptmenue
825 :
830 print"{clr}{blk}";:fori=0to39:print"C";:next
840 print"{wht} y="f$:print" im bereich von x="xu" bis x="xo
850 print" skaleneinheit auf dem bildschirm:
860 print" x-achse "xe*2,"y-achse "ye*2
870 print"{blk}";:fori=0to39:print"C";:next
880 print"{blk}die ausgabe erfolgt auf dem ";
890 ifaf=10thenprint"{rvon} plotter {rvof}":goto910
900 print"{rvon}bildschirm {rvof}"
910 print"{wht}w{blk}echsel des ausgabegeraetes {wht}w{blk}"
920 fori=0to39:print"C";:next
930 printtab(51)"{wht}welche aufgabe ?
940 printtab(40)"{wht}z{lgrn}eichnen der funktion"tab(38)"{wht}z"
950 printtab(40)"k{lgrn}urvendiskussion ausgeben"tab(38)"{wht}k"
960 printtab(40)"p{lgrn}arameter aendern"tab(38)"{wht}p"
970 printtab(40)"f{lgrn}unktion aendern"tab(38)"{wht}f"
980 printtab(40)"u{lgrn}mschalten auf grafikbildschirm"tab(38)"{wht}u"
990 printtab(40)"l{lgrn}oeschen des grafikbildschirms"tab(38)"{wht}l"
1000 printtab(40)"h{lgrn}ardcopy des grafikbildschirms"tab(38)"{wht}h"
1010 poke198,0:sys62255
1020 geta$:ifa$<>"w"then1050
1030 ifaf<>11thenaf=11:goto820
1040 ifaf<>10thenaf=10:goto820
1050 ifa$<>"z"then1080
1060 ifaf=10then1160
1070 sysein+3:sysfb,27:goto2020
1080 ifa$="f"then310
1090 ifa$="l"thensyscl:bs=0:goto1020
1100 ifa$="k"thenprint"{clr}":gosub1480:goto820
1110 ifa$="u"thensysein+3:sysfb,27:goto2320
1120 ifa$="h"thensysein+3:sysfb,27:gosub2520:sysof:goto820
1130 ifa$<>"p"then1020
1140 print"{clr}";
1150 syscl:goto590
1155 :
1160 rem kreuz plotten
1165 :
1170 open1,6,1:open2,6,2:open3,6,3:open10,6
1180 ifsvthen1330
1190 print#3,0:print#2,1
1200 print#10:print#1,"m";0;-440:print#1,"m";0;-200:print#10
1210 print#1,"m";80;yn:fori=0to14step2
1220 print#1,"i":print#1,"r";0;4:print#1,"j";0;-4
1230 print#1,"r";-12;-14
1240 print#10,int((xe*i+xu)*100+.5)/100;
1250 print#1,"m";80+i*25;yn:print#1,"d";80+(i+2)*25;yn
1260 next:print#1,"m";75+i*25;yn-4:print#10,">";
1270 print#1,"m";xn;-200
1280 fori=0to14step2:print#1,"i":print#1,"r";4;0
1290 print#1,"j";-4;0:print#1,"r";-30;-4
1300 j=yu+int(ye*100*i+.5)/100:ifj<>0thenprint#10,j;
1310 print#1,"m";xn;i*25-200:print#1,"d";xn;(i+2)*25-200
1320 next:print#1,"m";xn-5;i*25-209:print#3,1:print#10,"^";
1325 :
1330 rem kurve plotten
1335 :
1340 print"{clr}{blk}"tab(250)"etwas geduld bitte":print#2,sv+3
1350 e$="m":xw=xu:ifxu=0thenxw=1e-6
1360 gosub2340
1370 j=(xo-xu)/400:fori=0to400
1380 x=j*i+xw
1390 y=sin(x)+ sin(x*2):goto1410
1400 e$="m":goto1440
1410 y=y/ye*25+oy
1420 ify>210ory<-210thene$="m":goto1440
1430 print#1,e$;i+80;y:e$="d"
1440 next:gosub2350
1450 print#1,"m";0;180-sv*20:print#3,1:print#10,"y="f$;
1460 print#1,"m";0;-250
1470 sv=sv+1:sys62255:goto820
1480 rem kurvendiskussion ausgeben
1490 open1,6,1:open2,6,2:open3,6,3:open10,6:open11,3
1500 ifaf=10thenprint#1,"m";0;180-sv*25:print#3,0
1510 print"{clr}funktion:":printtab(6)"y="f$
1520 print#af
1530 print#af,"kurvendiskussion von x="xu"bis x="xo:print#af
1540 print#af," nullstellen:"
1550 s1=xe/5:gosub2340
1560 a=fnf(xu-1e-4)
1570 forx=xu+s1toxosteps1
1580 f=fnf(x)
1590 ifsgn(f)=sgn(a)then1720
1600 s=x-s1:z=x:c=x-s1/2
1610 fc=fnf(c)
1620 fz=fnf(z)
1630 ifsgn(fc)<>sgn(fz)thens=c:goto1650
1640 z=c
1650 c=(s+z)/2
1660 ifabs(z-s)>1e-6then1610
1670 fd=fnf1(c)
1680 ifabs(fc)<1e-4then1710
1690 ifabs(fd)>1e3thenprint#af," sprung bei x="int(c*1e4+.5)/1e4:goto1720
1700 goto1610
1710 print#af,tab(6)int(c*1e4+.5)/1e4;"/0","f'=";int((fd)*1e4+.5)/1e4
1720 a=f
1730 nextx
1740 print#af," extrema:":xw=xu
1750 a=fnf1(xw)
1760 forx=xu+s1toxosteps1
1770 f=fnf1(x)
1780 ifsgn(f)=sgn(a)then1940
1790 s=x-s1:z=x:c=x-s1/2
1800 fc=fnf1(c)
1810 fz=fnf1(z)
1820 ifsgn(fc)<>sgn(fz)thens=c:goto1840
1830 z=c
1840 c=(s+z)/2
1850 ifabs(z-s)>1e-5then1800
1860 ifabs(fc)<1e-2then1880
1870 goto1950
1880 fd=fnf2(c)
1890 ifabs(fd)<1e-5thenprint#af," sattel";:goto1920
1900 iffd>0thenprint#af," min.";:goto1920
1910 iffd<0thenprint#af," max.";
1920 fa=fnf(c):goto1930
1930 print#af,tab(7)int(c*1e4+.5)/1e4"/"int(fa*1e4+.5)/1e4:goto1950
1940 ifabs(f)<1e-6thenc=x:goto1890
1950 a=f:nextx:gosub2350:poke198,0:ifaf<>10then2000
1960 print#1,"m";0;-275
1970 printtab(15)"{rvon} fertig {rvof}{down}"
1980 print" in das gleiche achsenkreuz kann keine"
1990 print" weitere funktion geplottet werden !":wait198,1:goto820
2000 printtab(10)"{rvon}ende der ausgabe{rvof}":sys62255:wait198,1:return
2010 :
2020 rem ausgabe auf bildschirm
2030 :
2040 rem y-achse-zeichnen bs
2050 yk=(200-yn)*.5:ifyk<0thenyk=0
2060 ifyk>199thenyk=199
2070 ifbsthen2230
2080 bs=1:xk=(xn-80)*.5+60
2090 fory=0to199:sysan,xk,y:next
2100 un=xk-2
2120 fori=0to7
2130 forj=untoun+5:sysan,j,i*25:nextj,i
2140 un=yk-3:ifun<0thenun=0
2150 ifun+5>199thenun=194
2160 forx=60to259:sysan,x,yk:next
2170 fori=0to8:forj=untoun+5
2180 sysan,i*25+60,j
2190 nextj,i
2200 :
2210 rem kurve zeichnen bs
2220 :
2230 gosub2340:xw=xu:ifxw=0thenxw=1e-6
2240 j=(xo-xu)/200:yk=100-oy/2
2250 fori=1to200:x=j*i+xw
2260 y=sin(x)+ sin(x*2):goto2280
2270 goto2310
2280 y=yk-y/ye*12.5
2290 ify<0ory>199then2310
2300 sysan,i+60,y
2310 next:gosub2350
2320 poke198,0:wait198,1:sysof:goto820
2330 rem up fehlerroutine ein- aus
2340 poke768,23:poke769,193:return
2350 poke768,139:poke769,227:return
2360 rem up cursor positionieren
2370 poke211,x:poke214,y:sys58732:return
2380 :
2500 rem up hardcopy drucken
2510 :
2520 sys62255
2530 rem einsprung in das mp hardcopy:
2540 sys49440,8192,3
2550 sys62255:sysof
2555 rem hardcopy beschriften:
2560 open1,4:print#1:print#1
2565 print#1," funktion: y="f$
2570 print#1," skaleneinheit auf der x-achse:"xe*2
2580 print#1," y-achse:"ye*2
2590 print"{clr}"tab(240)" soll die kurvendiskussion ausgedruckt
2600 printtab(55)"werden ?":printtab(57)"j/n"
2610 geta$:ifa$="n"then2640
2620 ifa$<>"j"then2610
2630 af=1:gosub1510:af=11
2640 sys62255:return
5000 :
5010 rem erstellen des mp. feingrafik
5020 :
5030 fori=49152to49429
5040 readx:pokei,x:next
5050 data32,30,192,173,17,208,141,17,193,173,24,208,141,18,193,169,59,141,17
5060 data208,169,24,141,24,208,162,16,76,57,192,160,0,162,32,132,253,134,254
5070 data152,234,145,253,200,208,251,230,254,202,208,246,96,32,253,174,32,158
5080 data183,160,0,169,4,132,253,133,254,138,162,4,145,253,200,208,251,230,254
5090 data202,208,246,96,169,128,44,169,0,133,151,32,253,174,32,235,183,224,200
5100 data176,238,165,21,201,1,144,8,208,230,165,20,201,64,176,224,138,74,74
5110 data74,10,168,185,200,192,141,20,193,185,201,192,141,21,193,138,41,7,24
5120 data109,20,193,141,20,193,165,20,41,248,141,19,193,24,169,0,109,20,193
5130 data133,253,169,32,109,21,193,133,254,24,165,253,109,19,193,133,253,165
5140 data254,101,21,133,254,165,20,41,7,73,7,170,189,250,192,160,0,36,151,16
5150 data5,73,255,49,253,44,17,253,145,253,96,0,0,64,1,128,2,192,3,0,5,64,6
5160 data128,7,192,8,0,10,64,11,128,12,192,13,0,15,64,16,128,17,192,18,0,20
5170 data64,21,128,22,192,23,0,25,64,26,128,27,192,28,0,30,1,2,4,8,16,32,64
5180 data128,173,17,193,141,17,208,173,18,193,141,24,208,76,68,229,0,0,0,0,0
5190 rem erstellen fehlerroutine
5200 fori=49431to49439:readx:pokei,x:next
5210 data138,48,3,76,59,169,76,116,164
5220 return
5230 rem ende
PROGRAMM : MP 801 -49525- C174 C2BF ----------------------------------- C174 : 00 20 FD AE 20 9E B7 20 F0 C17C : C9 FF A2 1D 8E 74 C1 A9 78 C184 : 00 85 FB 85 FF A9 08 20 A4 C18C : D2 FF 20 E9 C1 A9 00 A0 4E C194 : C3 85 B0 84 B1 A9 0D 20 B3 C19C : D2 FF A9 28 85 15 A9 80 86 C1A4 : 85 97 A9 00 85 14 A0 06 E7 C1AC : B1 B0 25 97 F0 07 A5 14 F8 C1B4 : 19 E2 C1 85 14 88 10 F0 07 C1BC : A5 14 09 80 20 D2 FF 46 E3 C1C4 : 97 90 DF A5 B0 69 06 85 C9 C1CC : B0 90 02 E6 B1 C6 15 D0 69 C1D4 : CD CE 74 C1 D0 B4 A9 0D D1 C1DC : 20 D2 FF 4C CC FF 01 02 C4 C1E4 : 04 08 10 20 40 A0 27 84 A3 C1EC : FC A9 00 85 F8 A2 08 0A 46 C1F4 : 26 F8 06 FC 90 07 18 69 2C C1FC : 07 90 02 E6 F8 CA D0 EF B2 C204 : 85 F7 18 A5 FF 65 F7 85 56 C20C : F7 A9 C3 65 F8 85 F8 A9 68 C214 : 00 85 FA 98 C9 20 30 02 0B C21C : E6 FA 0A 0A 0A 85 F9 18 28 C224 : A5 FB 65 F9 85 F9 A9 00 2E C22C : 65 FA 85 FA 18 A9 20 65 E9 C234 : FA 85 FA A5 FB 4A 4A 4A 34 C23C : 85 FC 85 FD A9 00 85 FE 0F C244 : A2 08 0A 26 FE 06 FD 90 6B C24C : 07 18 69 38 90 02 E6 FE 73 C254 : CA D0 EF 85 FD 18 A5 FC 64 C25C : 65 FE 85 FE 18 A5 FD 65 F3 C264 : F9 85 F9 A5 FE 65 FA 85 65 C26C : FA A2 00 A5 01 85 02 A9 04 C274 : 36 85 01 A1 F9 81 F7 A5 B8 C27C : 02 85 01 88 30 03 4C EB B6 C284 : C1 A5 FB C9 C7 F0 12 E6 6A C28C : FB E6 FF A5 FF C9 07 F0 FB C294 : 03 4C E9 C1 A9 00 85 FF 21 C29C : 60 A9 C3 85 F8 A9 04 85 6A C2A4 : F7 A2 28 A9 00 A0 02 91 5C C2AC : F7 88 10 FB A5 F7 18 69 B8 C2B4 : 07 85 F7 90 02 E6 F8 CA 5F C2BC : D0 E9 60 D5
PROGRAMM : MP-802 -49440- C120 C453 ----------------------------------- C120 : 20 48 C1 E0 03 B0 28 86 54 C128 : FB 20 48 C1 E0 02 B0 1F 9D C130 : 86 FC A0 00 84 FD A4 FB 1F C138 : C0 02 F0 16 20 48 C1 E0 05 C140 : 29 B0 0C 86 FD 4C 52 C1 A4 C148 : 18 20 FD AE 4C 9E B7 4C F7 C150 : 48 B2 AD 02 DD 09 03 8D EA C158 : 02 DD 20 E7 FF A9 04 A2 F0 C160 : 04 A0 00 20 B4 C1 A9 05 C2 C168 : A2 04 A0 05 20 B4 C1 A9 D7 C170 : 06 A2 04 A0 06 20 B4 C1 94 C178 : A2 06 20 C9 FF A9 15 20 40 C180 : D2 FF A9 0D 20 D2 FF 20 37 C188 : CC FF A9 00 85 FE 85 72 09 C190 : AD 00 DD 49 FF 29 03 18 63 C198 : 6A 6A 6A 85 FF AD 11 D0 D6 C1A0 : 29 20 C9 20 D0 19 AD 18 0C C1A8 : D0 29 08 0A 0A 05 FF 85 24 C1B0 : FF 4C C2 C1 20 BA FF A9 E9 C1B8 : 00 20 BD FF 4C C0 FF 4C 9B C1C0 : 3E C2 A5 FB C9 02 F0 24 01 C1C8 : A9 00 85 71 20 E1 FF F0 F4 C1D0 : 18 20 B2 C2 F0 06 20 0B D3 C1D8 : C3 20 25 C3 20 47 C3 D0 5A C1E0 : EB 20 59 C3 20 66 C3 D0 90 C1E8 : DF 4C 8B C2 A5 FF 48 A5 EF C1F0 : FE 48 A9 00 85 71 20 E1 A5 C1F8 : FF F0 40 20 B2 C2 F0 09 9B C200 : 20 91 C3 20 0B C3 20 6D 08 C208 : C3 20 47 C3 D0 E8 20 59 AD C210 : C3 68 85 FE 68 85 FF A9 4E C218 : 00 85 71 20 E1 FF F0 1B 53 C220 : 20 B2 C2 F0 09 20 BC C3 74 C228 : 20 0B C3 20 6D C3 20 47 C7 C230 : C3 D0 E8 20 59 C3 20 66 9A C238 : C3 D0 B1 4C 8B C2 AD 18 0F C240 : D0 29 F0 4A 4A 05 FF 85 02 C248 : FF A2 06 20 C9 FF A9 18 91 C250 : 20 D2 FF A9 0D 20 D2 FF 2B C258 : 20 CC FF A2 04 20 C9 FF 9B C260 : A2 19 20 E1 FF F0 24 20 2B C268 : FF C3 A0 00 B1 FE 20 2F 63 C270 : C4 20 D2 FF C8 C0 28 D0 CE C278 : F3 A9 0D 20 D2 FF 98 18 47 C280 : 65 FE 85 FE 90 02 E6 FF 5A C288 : CA D0 D7 20 CC FF A2 06 18 C290 : 20 C9 FF A9 24 20 D2 FF 58 C298 : A9 0D 20 D2 FF 20 CC FF 5E C2A0 : A2 06 20 C3 FF A9 05 20 67 C2A8 : C3 FF A9 04 20 C3 FF 4C 0E C2B0 : E7 FF 78 A9 34 85 01 A9 B1 C2B8 : 00 AA 9D 34 03 E8 E0 08 06 C2C0 : D0 F8 A9 80 85 02 A0 00 72 C2C8 : B1 FE A2 00 0A 90 0A 48 7F C2D0 : BD 34 03 05 02 9D 34 03 ED C2D8 : 68 E8 E0 08 D0 EE 46 02 8F C2E0 : C8 C0 08 D0 E3 A9 37 85 98 C2E8 : 01 58 A5 FC F0 0F A2 00 30 C2F0 : BD 34 03 49 FF 9D 34 03 75 C2F8 : E8 E0 08 D0 F3 A9 00 AA 4E C300 : DD 34 03 D0 05 E8 E0 08 FD C308 : D0 F6 60 A2 05 20 C9 FF 38 C310 : A0 00 B9 34 03 20 D2 FF 22 C318 : C8 C0 08 D0 F5 A9 0D 20 7E C320 : D2 FF 4C CC FF A2 04 20 04 C328 : C9 FF 18 A5 FD 65 71 AA D2 C330 : F0 08 A9 20 20 D2 FF CA C1 C338 : D0 FA A9 FE 20 D2 FF A9 BB C340 : 8D 20 D2 FF 4C CC FF 18 ED C348 : A5 FE 69 08 85 FE 90 02 5E C350 : E6 FF E6 71 A5 71 C9 28 7B C358 : 60 A2 04 20 C9 FF A9 0D 6C C360 : 20 D2 FF 4C CC FF E6 72 C0 C368 : A5 72 C9 19 60 A2 04 20 47 C370 : C9 FF A9 0E 20 D2 FF A5 49 C378 : 71 AA F0 08 A9 20 20 D2 3D C380 : FF CA D0 FA A9 FE 20 D2 30 C388 : FF A9 8D 20 D2 FF 4C CC BB C390 : FF 20 F2 C3 A2 00 A9 C0 27 C398 : 85 02 B9 34 03 18 0A 90 4D C3A0 : 0A 48 A5 02 19 40 03 99 4B C3A8 : 40 03 68 46 02 46 02 E8 79 C3B0 : E0 04 D0 E9 C8 C0 08 D0 58 C3B8 : DB 4C E4 C3 20 F2 C3 A2 59 C3C0 : 00 A9 03 85 02 B9 34 03 CB C3C8 : 18 4A 90 0A 48 A5 02 19 57 C3D0 : 40 03 99 40 03 68 06 02 90 C3D8 : 06 02 E8 E0 04 D0 E9 C8 35 C3E0 : C0 08 D0 DB A0 00 B9 40 C5 C3E8 : 03 99 34 03 C8 C0 08 D0 7A C3F0 : F5 60 A9 00 AA 9D 40 03 1E C3F8 : E8 E0 08 D0 F8 A8 60 A5 0E C400 : FD F0 09 A8 A9 20 20 D2 8E C408 : FF 88 D0 FA AD 18 D0 29 10 C410 : 02 C9 02 D0 05 A9 11 20 B4 C418 : D2 FF A5 FB C9 02 D0 05 CD C420 : A9 0E 20 D2 FF A5 FC F0 36 C428 : 05 A9 12 20 D2 FF 60 29 8B C430 : 7F 48 29 20 D0 0A 68 48 B1 C438 : 29 40 D0 0C 68 09 40 60 C8 C440 : 68 48 29 40 D0 06 68 60 BE C448 : 68 09 20 60 68 29 3F 09 28 C450 : 80 60 00 09
PROGRAMM : HC EPSON 49440 C120 C330 ----------------------------------- C120 : 20 FD AE 20 8A AD 20 9B BC C128 : BC A5 65 F0 03 4C E3 A8 A2 C130 : A5 64 AA 29 10 D0 F6 8E 58 C138 : 78 C1 20 FD AE 20 9E B7 2E C140 : E0 04 30 03 4C AE B3 86 A5 C148 : AA 8A 29 80 30 F6 4C 55 28 C150 : C1 EA EA EA EA A9 00 85 A5 C158 : B7 85 A9 A9 01 A2 04 A0 E8 C160 : 04 20 BA FF 20 C0 FF A2 70 C168 : 01 20 C9 FF A2 06 BD ED 19 C170 : C2 20 D2 FF CA 10 F7 A9 57 C178 : 20 85 FC A9 00 85 FB 18 1B C180 : 69 40 85 FD A5 FC 69 1F 50 C188 : 85 FE A5 AA C9 02 10 05 42 C190 : A9 09 20 D2 FF A2 04 A5 91 C198 : AA C9 02 10 0B BD E3 C2 5D C1A0 : 20 D2 FF CA 10 F7 30 09 16 C1A8 : BD E8 C2 20 D2 FF CA 10 06 C1B0 : F7 A2 00 86 FF 20 18 C2 B0 C1B8 : A6 FF A5 FB 18 69 08 85 3F C1C0 : FB A5 FC 69 00 85 FC E8 EC C1C8 : E0 28 D0 E7 20 CC FF A2 9B C1D0 : 01 20 C9 FF A9 0A 20 D2 65 C1D8 : FF A5 AA C9 02 30 16 A6 D5 C1E0 : A9 D0 12 E6 A9 38 A5 FB 3E C1E8 : E9 40 85 FB A5 FC E9 01 BE C1F0 : 85 FC 4C 8A C1 A9 00 85 CC C1F8 : A9 A5 FC C5 FE D0 8B A5 5B C200 : FB C5 FD D0 85 A2 06 BD 78 C208 : F4 C2 20 D2 FF CA 10 F7 46 C210 : 20 CC FF A9 01 4C C3 FF 4D C218 : A5 01 48 78 A9 34 85 01 B3 C220 : A0 07 B1 FB 99 38 C3 A9 ED C228 : 00 99 30 C3 88 10 F3 68 23 C230 : 85 01 58 20 52 C2 A0 07 1C C238 : A5 AA C9 02 10 0A B9 30 7E C240 : C3 20 D2 C2 88 10 F7 60 CA C248 : B9 30 C3 20 88 C2 88 10 EF C250 : F7 60 A2 07 A0 07 B9 38 9A C258 : C3 29 80 20 78 C2 18 7D CD C260 : 30 C3 9D 30 C3 88 10 EE 7E C268 : A0 07 B9 38 C3 0A 99 38 65 C270 : C3 88 10 F6 CA 10 DD 60 C0 C278 : 85 02 98 C0 00 F0 05 46 65 C280 : 02 88 10 F7 A8 A5 02 60 4A C288 : 85 A8 98 48 A5 A9 F0 07 0A C290 : A0 04 06 A8 88 D0 FB A0 09 C298 : 00 84 A7 A5 A8 29 80 20 8F C2A0 : C6 C2 A5 A8 29 40 20 C5 E6 C2A8 : C2 A5 A8 29 20 4A 20 C5 EC C2B0 : C2 A5 A8 29 10 4A 4A 20 51 C2B8 : C5 C2 48 20 D2 C2 68 20 1A C2C0 : D2 C2 68 A8 60 4A 48 20 DC C2C8 : CC C2 68 4A 18 65 A7 85 AF C2D0 : A7 60 48 A5 AA 29 01 F0 48 C2D8 : 04 68 4C D2 FF 68 49 FF E6 C2E0 : 4C D2 FF 01 40 00 2A 1B 98 C2E8 : 02 80 04 2A 1B 00 0D 44 DF C2F0 : 1B 17 33 1B 0A 0A 0A 0A F4 C2F8 : 0A 32 1B 0D 48 41 52 44 E4 C300 : 43 4F 50 59 20 45 50 53 3E C308 : 4F 4E 0D 0D 28 43 29 20 E5 C310 : 20 4A 55 4E 49 20 31 39 41 C318 : 38 34 20 42 59 0D 46 52 76 C320 : 41 4E 4B 20 4C 4F 4E 43 5E C328 : 5A 45 57 53 4B 49 0D 00 98
