Leben und sterben lassen
»Life« ist wohl eine der faszinierendsten Simulationen von biologischen Vorgängen auf Computern. Mit »Life« lassen sich evolutionäre Abläufe spielerisch verstehen lernen.
Obwohl den Lesern der Inhalt des »Spiels« geläufig sein mag, hier die »Regeln«:
Es existiert ein zweidimensionales Feld und an jedem Punkt ist eine lebende oder eine tote Zelle. Jede Zelle hat acht Nachbarn.
An einem Punkt wird eine Zelle dann und nur dann lebendig, falls sie genau drei lebende Nachbarn hat.
Fast wie im richtigen Leben
Eine Zelle stirbt, wenn sie weniger als zwei (Vereinsamung) oder mehr als drei (Überbevölkerung) lebende Nachbarn hat.
So ändert sich das Feld von Generation zu Generation, mit einer meist faszinierenden Entwicklung. Das Spiel, erfunden von dem Mathematiker John Horton Conway (Cambridge), stellt sich als höchst komplex und reizvoll heraus.
Um es gleich zu sagen: Life ist kein Spiel, das man selber spielt. Life spielt sich selbst. Man kann die »Anfangswelt« festlegen und dann beobachten, wie sie sich entwickelt. Das Spiel wird sicher dem einen oder anderen Computer-Fan bekannt sein, da es ein ideales Problem für den Computer ist: Sehr einfache Regeln, aber viel Rechnerei.
In dem Beispiel (Rotor, siehe Bild 1) sind die Verhältnisse noch sehr einfach, weil die kleine Life-Welt nur zwischen zwei Zuständen hin und her pendelt. Dieser Dreier ist eine der Strukturen, die stabil sind. Meistens dauert es viele Generationen, bis eine Population ausstirbt oder in stabile Strukturen übergeht. Am besten, man experimentiert einfach etwas. Bild 2 zeigt noch einige interessante Strukturen.
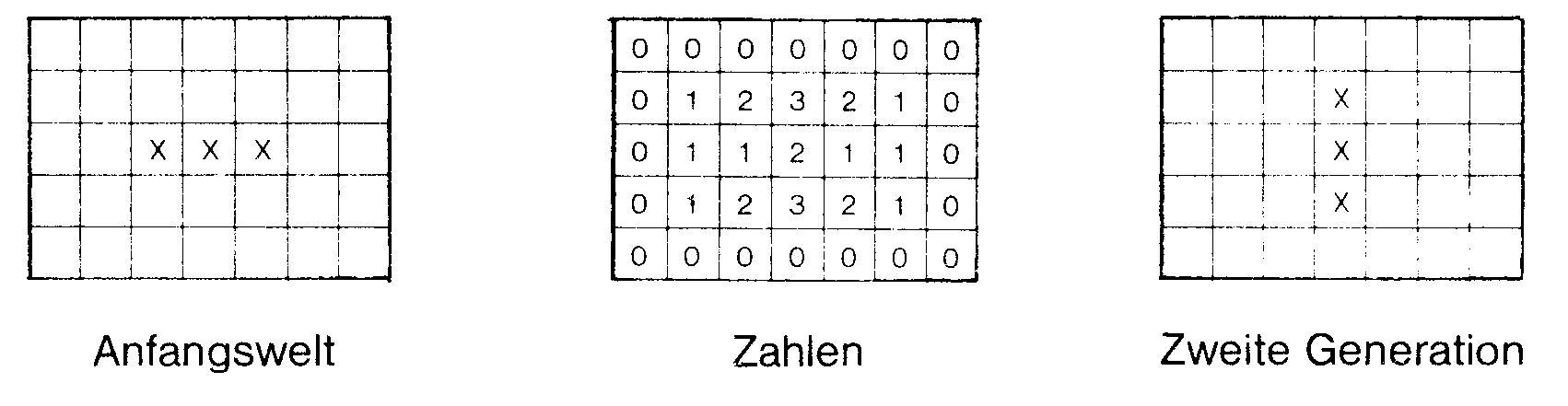
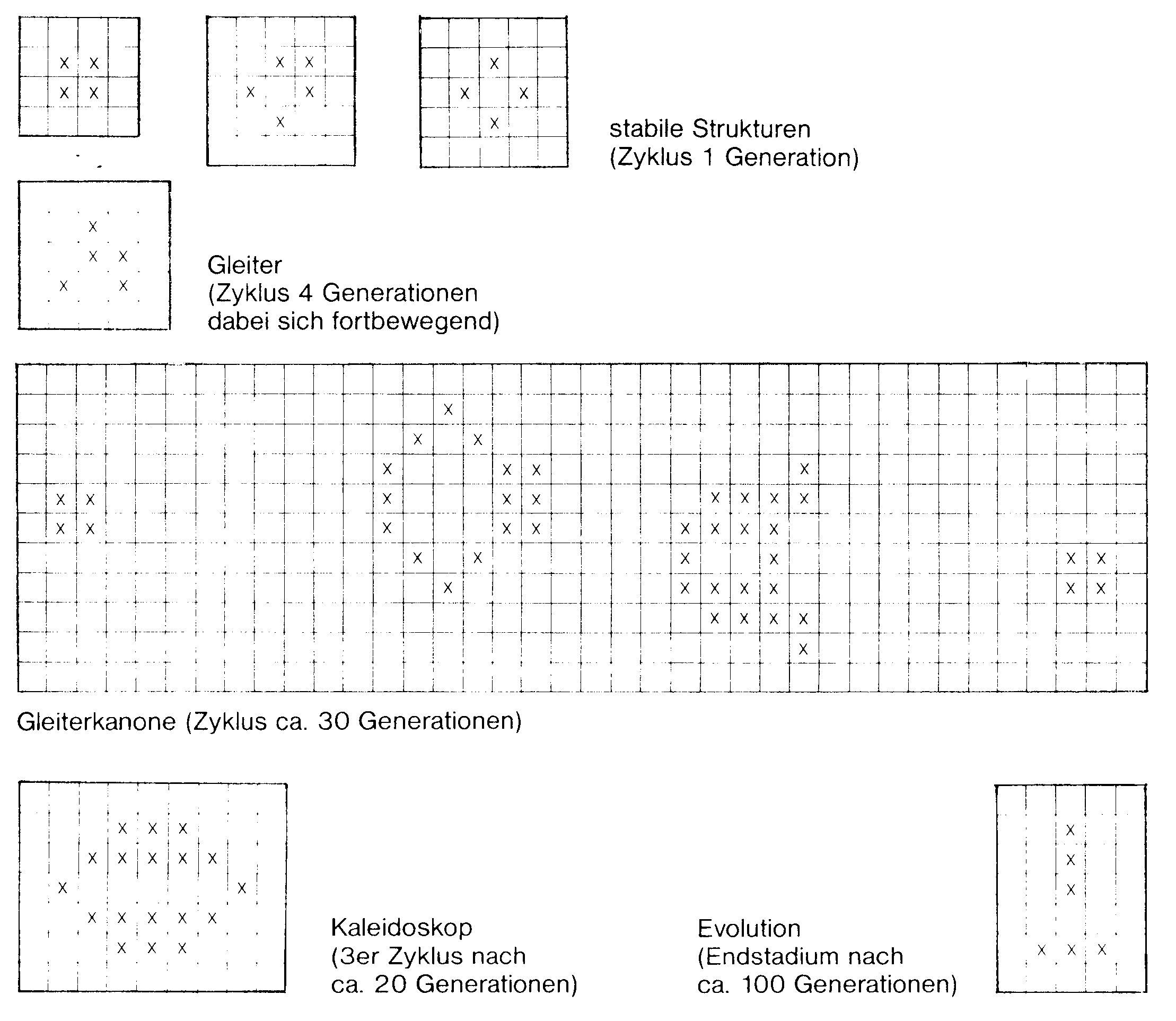
Zum Programm:
Wie würde man das Problem normalerweise angehen? Nun, man legt sich ein zweidimensionales Feld an und speichert für jede lebende Zelle eine Eins, für jedes unbesetzte Kästchen eine Null. Dann geht man alle Felder durch, prüft die acht Nachbarfelder und speichert das Ergebnis, tot oder lebendig in der nächsten Generation, in einem zweiten Feld. Der Computer hat dann (bei 80 mal 50) 32 000 Felder zu überprüfen, und das bedeutet: warten…
Aber Moment! Ist es denn nötig, auch die Bereiche zu bearbeiten, in denen es ohnehin kein Leben gibt?
Besser, man bearbeitet jeweils nur die relevanten (belebten) Bereiche: Es kann nur in dem Bereich etwas passieren, der direkt an lebende Zellen angrenzt. Man speichert die Koordinaten aller lebenden Zellen und ihrer Nachbarn, sorgt dafür, daß keine Felder doppelt gezählt werden und braucht dann jeweils nur noch die Liste der Koordinaten durchzugehen. Dafür benötigt man ein weiteres Variablen-Feld, in dem bereits vermerkte Zellen gekennzeichnet werden. Nach dieser Vorbereitung werden zur Berechnung der nächsten Generation die Koordinaten des relevanten Bereichs durchgegangen. Ein zweites Mal durchläuft man die Koordinaten, um den neuen relevanten Bereich festzustellen. Wenn also eine Struktur auf dem Bildschirm wandert, so wandert auch der relevante Bereich mit.
Bedienungshinweise:
Man hat eine 78 x 48-Auflösung (der äußerste Rand ist eine Todeszone«; hier ist grundsätzlich kein Leben möglich) zur Verfügung. Startet man das Programm, so befindet man sich in einem Editor.
Eine Zelle wird mit der SPACE-Taste lebendig.
Eine Zelle wird mit der DEL-Taste getötet.
Der Cursor schreitet nach SPACE und DEL in die Richtung fort, die die letzte gedrückte Cursortaste angab.
Mit »L« wird Life dann gestartet. In dem jetzigen Zustand gibt es folgende Befehle:
| S | Stop |
| F1-F8 | Verzögerung |
| N | Neue Eingabe |
| E | Ergänzung, Veränderung |
| Q | Quit, Programmende |
| P | Power, maximale Geschwindigkeit (nur mit RUN-STOP/RESTORE zu lösen) |
Erweiterungsmöglichkeiten:
Man könnte natürlich die Auflösung weiter erhöhen. Da böte sich dann die Bitmap-Auflösung an (HiRes-Grafik). Hier müßte man allerdings mit dem Speicherplatz sehr vorsichtig umgehen, da der Bildschirm 64000 Bildpunkte hat. Die zusätzlichen Berechnungen würden das Programm auf jeden Fall langsamer machen. Außerdem wird, wenn die relevanten Bereiche zu groß werden, ein Speichern derselben unmöglich (Speicherplatz) und der Generationswechsel dauert zu lange. Eine andere interessante Veränderung wäre mit dem Rand durchzuführen. Mit dem »Todesrand« wurde das Problem der Bildschirm-Bereichsüberschreitung zwar recht elegant gelöst, denn es sind durch das Prinzip der relevanten Bereiche keine Abfragen notwendig. Interessanter jedoch wäre eine offene Wand oder gar eine ganz in sich geschlossene Welt. Unten (rechts) heraustretende Formen würden dann oben (links) wieder auftauchen. Wegen der Abfragen würde jedoch auch dies die Geschwindigkeit verringern.
Hinweise zum Abtippen:
Als erstes geben Sie die Maschinenroutine (Listing 2) mit dem MSE ein (Speichern nicht vergessen). Zur Eingabe des Hauptprogramms (Listing 1) verwenden Sie bitte den Checksummer.
Interessierte Leser finden in der Tabelle 1 die Beschreibung des Maschinenprogramms.
Wer will, kann das Programm noch wesentlich erweitern: Zum Beispiel könnten Hungersnöte, Naturkatastrophen oder Seuchen in bestimmten Gebieten die Bevölkerung wesentlich dezimieren. Ich glaube nicht, daß man das Spiel »Life« auf dem C 64 noch wesentlich schneller programmieren kann, jedoch soll diese Behauptung ruhig dazu provozieren, das Gegenteil zu beweisen.
(Jürgen Engbring/tr)| Routinen des Maschinenprogramms | ||
| $C000-C023 | 16-Bit-Multiplikation (Listing 2) | |
| $C024-C067 | Rechnung: 6000+3 (X+40 Y)→SP(16B) | |
| $C068-C079 | Rechnung: 4 S(16B)→SP1(16B) | |
| $C080-C097 | Rechnung: 4 M(16B)→SP1(16B) | |
| $C098-C0A5 | Inkrement X | Verändert SP(16B) entsprechend, so daß es dem Ergebnis der Routine $C024 entspricht. |
| $C0A6-C0B3 | Inkrement Y | |
| $C0B4-C0C1 | Dekrement X | |
| $C0C2-C0CF | Dekrement Y | |
| $C0D0-C0DC | erhöht M, falls Zelle bei X,Y lebt | |
| $C0DD-C104 | relevanter Bereich, speichert Koordinaten | |
| $C105-C15C | relevanter Bereich, geht neun Umgebungszellen durch, ruft $C0DD auf | |
| $C15D-C2A4 | nächste Generation, läuft zweimal durch alle Koordinaten des relevanten Bereichs | |
| $C2A5-C332 | colspan="2"Plot: setzt, löscht und prüft Punkte im 80 x 50-Bild | |
| $C333-C3A6 | Initialisierungsroutine | |
| $C3A7-C3C4 | Aufruf relevanter Bereich, setzt A%(X,Y)=1, trägt Koordinaten der Umgebungsfelder ein (SYS C3A7,X,Y) | |
| $C3C5-C3F6 | Aufruf Plot, SYS C3C5,X,Y,Z, löscht, setzt (Z30 = oder 1) oder kontrolliert (Z=2) Punkte | |
| $C3F7-C3FC | Aufruf nächste Generation, ruft $C15D auf, setzt zwecks Beschleunigung Interrupt-Flag | |
| $C3FD-C403 | Aufruf maximale Geschwindigkeit, setzt I-Flag, ruft in Endlosschleife $C15D | |
| Variablen des Maschinenprogramms | ||
| $C404-C413 | Tabelle Binärzahlen→ASCII-Code (der Grafikzeichen für Plot) | |
| $C414 | Z (siehe $C3C5), enthält wegen logischen Verknüpfungen 00 für setzen und $0F für löschen | |
| $C415 | L gibt an, welches Bit des Grafikzeichens angesprochen wird | |
| $C416 | QQ liefert Ergebnis des Tests | |
| $C417/8 | X/Y | |
| $C419/B | Zwischenspeicher 1/2 | |
| $C41A | E gibt an, welcher A%() Speicherbedarf angesprochen wird | |
| $C41C/D | M(16B) | Zahl der Koordinaten beziehungsweise Schleifenindex |
| $C41E/F | S(16B) | |
| $C420 | M Zahl der lebenden Zellen in jeweiliger Umgebung | |
| $C421 | J gibt an, welcher X%,Y% Speicherbetrieb angesprochen wird | |
| $C422-C521 | Tabelle ASCII-Code→Binärzahlen (wird erzeugt) | |
| $57-5B | für 16-Bit-Multiplikation (5B)x(59/5A)=(57/58) | |
| $57/58 | SP(16B) (lokal) | |
| $59/5A | SP1(16B) (lokal) | |
S(16B) bedeutet Speicher S mit der Länge von 16 Bit. X und Y haben nichts mit den Registern zu tun, die Namen der Variablen beziehen sich auf das Basic-Programm (Listing 1)
10 rem-------------------------
20 rem** life fuer c-64 **
25 rem-------------------------
30 rem** juergen engbring **
40 rem** henkelshof 5-7 **
50 rem** 5630 remscheid-11 **
60 rem** tel. 02191/65533 **
70 rem-------------------------
80 m=49152:fori=0to9:reada
85 ifa<>peek(m)thenload"maschlife",8,1
90 m=m+100:next
95 data169,88,87,206,2,152,0,192,45,0
100 print"{clr}"
110 sys49971: rem initialisierung
120 pl=50117: rem syspl,x,y,0/1/2
130 :n=50167: rem naechste generation
140 :s=50173: rem maximale geschw.
150 :g=50087: rem sysg,x,y zelle lebt
155 ba=6*4096:rem basis zellspeicher
160 qq=50198: rem testbyte syspl,x,y,2
170 rem+++++++++++++++++++++++++++++++++
990 rem=== 80 x 40 zelleditor ========
1000 dimg%(255):x=39:y=24:q=ti:ch=29
1005 fori=0to6:reada:readb:g%(a)=b:next
1010 data17,1,29,2,145,3,157,4,20,5,32,6,76,7
1020 geta$:ifti-q>15thenq=ti:w=1-w
1030 syspl,x,y,w
1040 ifa$=""then1020
1050 a=asc(a$)
1060 ong%(a)goto1100,1200,1300,1400,1500,1600,1700
1070 goto1020
1100 syspl,x,y,z:y=y+1:ch=17
1110 ify>49theny=0
1120 goto1450
1200 syspl,x,y,z:x=x+1:ch=29
1210 ifx>79thenx=0
1220 goto1450
1300 syspl,x,y,z:y=y-1:ch=145
1310 ify<0theny=49
1320 goto1450
1400 syspl,x,y,z:x=x-1:ch=157
1410 ifx<0thenx=79
1420 goto1450
1450 syspl,x,y,2:z=peek(qq)
1460 goto1020
1500 z=0:a=ch:pokeba+3*x+y*240,0
1510 goto1060
1600 z=1:a=ch
1610 sysg,x,y:goto1060
1700 syspl,x,y,z
2000 t=9999:rem minimale verzoegerung
2005 poke50209,2:rem vor erstem sysn
2010 geta$:ifti-q>tthenq=ti:sysn
2020 ifa$=""then2010
2030 ifa$=" "thensysn:t=9999:goto2010
2040 ifa$="s"thent=99999
2050 ifa$="n"thenrun
2055 ifa$="e"goto2300
2060 ifa$="q"then:end
2065 ifa$="p"thensyss
2067 ifa$=chr$(133)goto2200
2070 a=asc(a$)
2080 ifa<134ora>140goto2010
2090 t=2*2^(a-134)
2100 goto2010
2200 geta$:ifa$=""thensysn:goto2200
2210 goto2020
2300 ifpeek(50202)=1thensysn
2310 poke50209,0:goto1020
PROGRAMM : MASCHLIFE C000 C414 ----------------------------------- C000 : A9 00 85 57 85 58 A0 08 A3 C008 : 18 26 5B 90 0D 18 A5 57 F3 C010 : 65 59 85 57 A5 58 65 5A D5 C018 : 85 58 88 F0 06 26 57 26 45 C020 : 58 90 E6 60 A9 50 85 5B 70 C028 : A9 00 85 5A AD 18 C4 85 38 C030 : 59 20 00 C0 AD 17 C4 18 88 C038 : 65 57 85 57 A9 00 65 58 76 C040 : 85 58 A5 57 85 59 A5 58 B0 C048 : 85 5A 06 57 26 58 18 A5 38 C050 : 59 65 57 85 57 A5 5A 65 B9 C058 : 58 85 58 A9 00 65 57 85 52 C060 : 57 A9 60 65 58 85 58 60 24 C068 : AD 1E C4 0A 85 59 AD 1F AF C070 : C4 2A 85 5A 06 59 26 5A 6E C078 : 18 A9 40 65 5A 85 5A 60 1E C080 : AD 1C C4 0A 85 59 AD 1D C2 C088 : C4 2A 85 5A 06 59 26 5A 86 C090 : 18 A9 40 65 5A 85 5A 60 36 C098 : 18 A9 03 65 57 85 57 A9 45 C0A0 : 00 65 58 85 58 60 18 A9 56 C0A8 : F0 65 57 85 57 A9 00 65 5F C0B0 : 58 85 58 60 38 A5 57 E9 CF C0B8 : 03 85 57 A5 58 E9 00 85 E8 C0C0 : 58 60 38 A5 57 E9 F0 85 9F C0C8 : 57 A5 58 E9 00 85 58 60 93 C0D0 : AC 1A C4 B1 57 C9 01 D0 5A C0D8 : 03 EE 20 C4 60 A0 02 B1 69 C0E0 : 57 C9 01 F0 1F A9 01 A0 FF C0E8 : 02 91 57 20 80 C0 AD 17 80 C0F0 : C4 AC 21 C4 91 59 C8 AD 4E C0F8 : 18 C4 91 59 EE 1C C4 D0 86 C100 : 03 EE 1D C4 60 20 DD C0 5A C108 : EE 17 C4 20 98 C0 20 DD 83 C110 : C0 EE 18 C4 20 A6 C0 20 60 C118 : DD C0 CE 17 C4 20 B4 C0 8D C120 : 20 DD C0 CE 17 C4 20 B4 BA C128 : C0 20 DD C0 CE 18 C4 20 89 C130 : C2 C0 20 DD C0 CE 18 C4 82 C138 : 20 C2 C0 20 DD C0 EE 17 BB C140 : C4 20 98 C0 20 DD C0 EE 24 C148 : 17 C4 20 98 C0 20 DD C0 E2 C150 : CE 17 C4 EE 18 C4 20 B4 4A C158 : C0 20 A6 C0 60 CE 1C C4 60 C160 : AD 1C C4 8D 1E C4 C9 FF 2D C168 : D0 03 CE 1D C4 AD 1D C4 C9 C170 : 8D 1F C4 20 80 C0 AD 21 C9 C178 : C4 49 02 A8 B1 59 8D 17 C1 C180 : C4 C8 B1 59 8D 18 C4 20 2D C188 : 24 C0 A9 00 8D 20 C4 A0 A5 C190 : 02 91 57 EE 17 C4 20 98 58 C198 : C0 20 D0 C0 EE 18 C4 20 B7 C1A0 : A6 C0 20 D0 C0 CE 17 C4 31 C1A8 : 20 B4 C0 20 D0 C0 CE 17 D3 C1B0 : C4 20 B4 C0 20 D0 C0 CE F3 C1B8 : 18 C4 20 C2 C0 20 D0 C0 65 C1C0 : CE 18 C4 20 C2 C0 20 D0 24 C1C8 : C0 EE 17 C4 20 98 C0 20 68 C1D0 : D0 C0 EE 17 C4 20 98 C0 D0 C1D8 : 20 D0 C0 CE 17 C4 EE 18 EE C1E0 : C4 20 A6 C0 20 B4 C0 AD 7C C1E8 : 20 C4 C9 02 D0 10 AC 1A 91 C1F0 : C4 B1 57 AA 98 49 01 A8 E1 C1F8 : 8A 91 57 4C 12 C2 A2 00 6C C200 : AD 20 C4 C9 03 D0 02 A2 2C C208 : 01 AD 1A C4 49 01 A8 8A 53 C210 : 91 57 CE 1C C4 A9 FF CD B9 C218 : 1C C4 D0 08 CE 1D C4 10 D4 C220 : 03 4C 27 C2 4C 73 C1 A9 26 C228 : 00 8D 1C C4 8D 1D C4 20 A4 C230 : 68 C0 AD 21 C4 49 02 A8 78 C238 : B1 59 8D 17 C4 C8 B1 59 E8 C240 : 8D 18 C4 20 24 C0 AD 1A 42 C248 : C4 49 01 A8 B1 57 8D 1B 48 C250 : C4 8D 14 C4 AC 1A C4 A9 7A C258 : 00 91 57 AD 1B C4 C9 01 AD C260 : D0 03 20 05 C1 AD 14 C4 BE C268 : C9 01 F0 0B A9 0F 8D 14 C1 C270 : C4 20 A5 C2 4C 7F C2 A9 25 C278 : 00 8D 14 C4 20 A5 C2 CE B4 C280 : 1E C4 AD 1E C4 C9 FF D0 6C C288 : 08 CE 1F C4 10 03 4C 94 CB C290 : C2 4C 2F C2 AD 1A C4 49 EE C298 : 01 8D 1A C4 AD 21 C4 49 08 C2A0 : 02 8D 21 C4 60 AD 17 C4 A3 C2A8 : 4A 8D 19 C4 AD 18 C4 4A DB C2B0 : 85 5B A9 00 85 5A A9 28 6F C2B8 : 85 59 20 00 C0 A9 04 18 8C C2C0 : 65 58 18 AD 19 C4 65 57 09 C2C8 : 85 57 A9 04 65 58 85 58 C4 C2D0 : AD 17 C4 29 01 F0 11 AD 96 C2D8 : 18 C4 29 01 F0 05 A9 01 9D C2E0 : 4C F6 C2 A9 04 4C F6 C2 91 C2E8 : AD 18 C4 29 01 F0 05 A9 F7 C2F0 : 02 4C F6 C2 A9 08 8D 15 69 C2F8 : C4 AD 14 C4 C9 FF F0 18 C1 C300 : A0 00 B1 57 AA BD 22 C4 A2 C308 : 4D 14 C4 0D 15 C4 4D 14 07 C310 : C4 AA BD 04 C4 91 57 60 10 C318 : A0 00 B1 57 AA BD 22 C4 BA C320 : 2D 15 C4 F0 08 A9 01 8D 14 C328 : 16 C4 4C 32 C3 A9 00 8D 9E C330 : 16 C4 60 A9 00 85 59 A9 DA C338 : 8E 85 5A A2 4E A0 DF A9 30 C340 : 00 91 59 88 D0 F9 C6 5A 1D C348 : CA 10 F6 A9 00 85 57 A9 EA C350 : 60 85 58 A0 EF A2 4F A9 42 C358 : 01 91 57 88 88 88 CA 10 21 C360 : F8 A2 30 A0 02 A9 01 91 5E C368 : 57 A0 EF 91 57 20 A6 C0 D0 C370 : CA 10 F0 A9 01 A0 EF A2 CE C378 : 4F 91 57 88 88 88 CA 10 8F C380 : F8 A2 00 A9 00 9D 22 C4 FE C388 : CA D0 FA A2 0F BD 04 C4 46 C390 : A8 8A 99 22 C4 CA 10 F5 F7 C398 : A9 00 8D 21 C4 8D 1A C4 73 C3A0 : 8D 1C C4 8D 1D C4 60 20 D8 C3A8 : FD AE 20 9E B7 8E 17 C4 AE C3B0 : 20 FD AE 20 9E B7 8E 18 91 C3B8 : C4 20 24 C0 A0 00 A9 01 60 C3C0 : 91 57 4C 05 C1 20 FD AE 23 C3C8 : 20 9E B7 8E 17 C4 20 FD 0B C3D0 : AE 20 9E B7 8E 18 C4 20 2A C3D8 : FD AE 20 9E B7 E0 01 F0 71 C3E0 : 09 E0 02 F0 0A A9 0F 4C BB C3E8 : F1 C3 A9 00 4C F1 C3 A9 DC C3F0 : FF 8D 14 C4 4C A5 C2 78 41 C3F8 : 20 5D C1 58 60 78 20 5D 47 C400 : C1 4C FE C3 20 6C 7B 62 37 C408 : 7C E1 FF FE 7E 7F 61 FC B8 C410 : E2 FB EC A0 04
