Streifzüge durch die Grafikwelt (Teil 3)
C 128-Besitzer aufgepaßt: Eine Teilnahme an den Streifzügen ist auch für Sie möglich. Durch die »Übersetzung« des Standards starten auch Sie mit uns in der nullten Dimension.
Viele von Ihnen werden das neue Flaggschiff von Commodore, den C 128, schon vor sich stehen haben. Damit Sie nicht immer bei der Umsetzung der Beispielprogramme in den C 64-Modus schalten müssen, um HIRES-3 zu verwenden, soll hier die Übersetzung der von uns verwendeten, allgemeinen Grafikbefehle in das Basic 7.0 dieses Computers besprochen werden.
Der C 128 und unser Standard
Der erste Befehl (»INIT«), der die Initialisierung der Grafik (Bitmap einrichten, löschen und Farbgebung) bewirken soll, ist so umzusetzen:
COLOR 0,16 : COLOR 1,7 : COLOR 4,1 : GRAPHIC 1,1
Komplizierter wird es da leider beim »START«-Befehl. Dieser soll das Grafiksystem in einen definierten Ausgangszustand bringen. Der Ursprung des Bildschirmsystems soll nach »START« in der Ecke links unten liegen und in der Horizontalen müssen 320, in der Vertikalen 200 Bildkoordinaten zur Verfügung stehen. Leider ist auch der Grafikbildschirm des C 128 so eingerichtet, daß von links oben an gezählt wird und die Y-Achse nach unten zeigt. Der »SCALE«-Befehl im Basic 7.0 erlaubt zwar die Skalierung der beiden Achsen bis zu Maximalwerten von 32767 (im Gegensatz zu den Angaben im Handbuch, wo maximal 1023 erwähnt sind). Es gibt aber keine Möglichkeit, das Koordinatensystem zu verschieben. Man muß sich also leider wieder mit einer Transformation begnügen, was — solange wir dazu nicht wieder ein Assemblerprogramm haben wie in HIRES-3 — natürlich Rechenzeit beansprucht.
In Listing 1 finden Sie ein kleines Unterprogramm, das — ausgehend von den schon aus HIRES-3 bekannten Systemgrenzwerten XU,XO,YU und YO (kleinste/größte X-, beziehungsweise Y-Koordinate) — aus den eingegebenen Koordinaten X und Y die Bildschirmkoordinaten XX und YY berechnet. Nun ist es relativ einfach, durch Festlegung dieser Systemgrenzwerte den Befehl »START« zu realisieren:
XU=0 : XO=319 : YU=0 : YO=199
Ebenfalls mit Hilfe des Transformations-Unterprogrammes kann die Grafikanweisung »MITTE« übersetzt werden durch Definieren von:
XU=-160 : XO=160 : YU=-100 : YG=100
Durch die Notwendigkeit der Transformation muß nun jede weitere Punktkoordinate vor dem jeweiligen Grafikbefehl durch unser Unterprogramm laufen. Der Grafik-Befehl »PUNKT (X,Y)« lautet dann:
GOSUB 1020 : DRAW 1,XX,YY
Für »LINIE (XA,YA,XB,YB)« steht beim C 128:
X=XA : Y=YA : GOSUB 1020 : X1=XX : Y1=YY
X = XB : Y=YB : GOSUB 1020 : X2=XX : Y2=YY
DRAW 1,X1,Y1 TO X2,Y2
Für »KREIS (XM,YM,RX,RY> muß der Mittelpunkt anders transformiert werden als die Halbmesser: X=XM : Y=YM : GOSUB 1020 : X5=XX: Y5=YY RX=RX*319/(XO-XU) : RY=RY*199/(YO-YU) CIRCLE 1,X5,Y5,RX,RY
Die weiteren Übersetzungen:
- TEXT (A$,XT,YT) entspricht CHAR 1,XT,YT,A$
- SHOW entspricht GRAPHIC1
- NORMAL entspricht GRAPHIC0
- GRESET entspricht SCNCLR(1)
Damit ergeben sich die C 128-Versionen der beiden Programme aus der letzten Folge (Fensterrose und Spiralen), die hier als Listing 2 und Listing 3 abgedruckt sind.
In Tabelle 1 finden Sie eine Übersicht über alle Grafikbefehle und ihre Übersetzungen in die drei Systeme: C 64 + HIRES-3, Plotter 1520, C 128 Basic 7.0.
| Befehl | HIRES-3 auf C 64 | Plotter 1520 | C 128 Basic 7.0 |
| INIT | POKE 53280,0:SYS37498:HFL,6,12 | OPEN1,6,1:OPEN2,6,2:PRINT#2,0:CLOSE2 | COLOR,16:COLOR1,7:COLOR4,1:GRAPHIC1,1 |
| START | TRS,0,320,0,200 | PRINT#1,"M",0,-200:PRINT#1,"J" | XU=0:XO=319:YU=0:YO=199 Bezogen auf das UP Transformation |
| MITTE | TRS,-160,160,-100,100 | PRINT#1,"R",240,0:PRINT#1,"J" | XU=-160:XO=160:YU=-100:YO=100 Bezogen auf das UP Transformation |
| PUNKT (X,Y) | TPK,X,Y | PRINT#1,"R",X,Y:PRINT#1,"J",X+2,Y+2:PRINT#1,"R",X,Y | GOSUB 1020:DRAW1,XX,YY UP Transformation ab 1020 |
| LINE (XA,YA,XB,YB) | TLN,XA,YA,XB,YB | PRINT#,"R",XA,YA:PRINT#1,"J",XB,YB | X=XA:Y=YA:GOSUB 1020:XF=XX:Y1=YY:X=XB:Y=YB:GOSUB 1020:X2=XX:Y2=YY:DRAW1,X1,Y1 TO X2,Y2 UP Transformation ab 1020 |
| KREIS (XM,YM,RX,RY) | TKR,XM,YM,RX,RY,2*π | PROGRAMM: M=50:D=360⋅π/(M⋅180):DIMT(M):T(O)=2⋅π:FORJ=1 TO M:T(J)=T(J-1)+D:PRINT#1,"R",RX⋅COS(T(J-1))+XM,RY⋅SIN(T(J-1))+YM:PRINT#1,"J",RX⋅COS(T(J))+XM,RY⋅SIN(T(J))+YM:NEXTJ |
X=XM:Y=YM:GOSUB 1020:X5=XX:Y5=YY:RX=⋅319/(XO-XU):RY=RY⋅199/(YO-YU):CIRCLE1,X5,Y5,RX,RY UP Transformation ab 1020 |
| TEXT (A$,XT,YT) | TEX,A$,YT,XT | OPEN4,6:PRINT#1,"R",XT,YT:PRINT#4,A$:CLOSE4:PRINT#1,"M",240,-YT:PRINT # 1,"J" | CHAR1,XT,YT,A$ |
| SHOW | HAN | PRINT#1,"R",O,-200 | GRAPHIC1 |
| NORMAL | HOF | CLOSE1 | GRAPHIC0 |
| GRESET | LOE:AUS | OPEN7,6,7:PRINT#7:CLOSE7 | SCNCLR(1) |
Grafikstandardprobleme
Nicht daß Sie denken, der Sinn für Proportionen sei uns abhanden gekommen, weil sich dieses Kapitel mit verschiedenen Grafikstandards (kurz GKS genannt) in bezug auf unsere Computer befaßt: Es scheint mir aber doch notwendig, zumindest einmal kurz das Verhältnis beispielsweise des GKS und ähnlicher Normen des hier verwendeten Minimal-Grafik-Sprachschatzes anzureißen.
Bemühungen, eine geräteunabhängige Grafikschnittstelle softwaremäßig zu realisieren, gibt es schon geraume Zeit. In den USA existiert das System CORE, in Deutschland wurde vor einiger Zeit ein GKS als DIN-Entwurf vorgelegt. Beide sind von Haus aus für Großrechenanlagen entwickelt worden und wurden von dem rasanten technischen Fortschritt überholt, der Mikro-, Personal- und sogar Homecomputer im Feld der professionellen Grafikprogrammierung auftauchen ließ. IBM versucht, für den IBM/AT eine GKS-Implementierung zu erstellen. Die erforderlichen Rechenkapazitäten für GKS und auch CORE sind aber relativ hoch, weshalb eine Verwendung dieser Standards bislang nur auf leistungsfähigen Großcomputern oder 32-Bit-Geräten mit arithmetischen Coprozessoren sinnvoll ist. Einem 8-Bit-Computer sind Grenzen gesetzt, die es allenfalls erlauben, eine minimale Teilmenge des Standardwortschatzes anzustreben.
Die Frage ist, ob das wünschenswert erscheint. Dazu einige Erklärungen: Man kann grob zwei grundlegende Arten von Grafik-Befehlen unterscheiden, nämlich einmal mit und einmal ohne einen Grafik-Cursor. Im ersten Fall gleitet der »Zeichenstift« immer von der aktuellen Position des — häufig nur gedachten — Cursors zeichnend oder nicht zeichnend zur angegebenen neuen Position. Im anderen Fall existiert solch eine Cursorposition nicht. Alle Größen, die zur Ausführung eines Befehls wie LINIE nötig sind, werden mit diesem als Argument übergeben.
Im CORE-System (auch im GKS) gibt es beispielsweise folgende Befehle:
LINE-ABS-2(X,Y):Zieht eine Linie von der aktuellen Cursorposition bis X,Y. Die 2 kommt von 2D, also einem ebenen Koordinatensystem mit zwei Achsen.
LINE-REL-2(DX,DY):Zieht von der Cursorposition aus eine Linie zu einem Punkt, dessen Koordinaten um DX und DY von der Cursorposition verschieden sind.
MOVE-ABS-2(X,Y):Der Cursor wird nicht-zeichnend von der aktuellen Position zum Punkt X,Y bewegt.
MOVE-REL-2(DX,DY):Wie beim entsprechenden LINE-Befehl, aber nicht zeichnend.
Auf dem C 128 können wir auch diese Art der Grafikprogrammierung durchführen. Die Entsprechungen wären (in der gleichen Reihenfolge):
DRAW1 TO X,Y
DRAW1 TO (RDOT(0)+DX), (RDOT(1)+DY)
LOCATE X,Y
LOCATE (RDOT(0)+DX), (RDOT(1)+DY)
Sehen wir uns den Unterschied am Beispiel in Bild 1 an, wo ein Haus auf den normalen Commodore-Bildschirm gezeichnet werden soll.
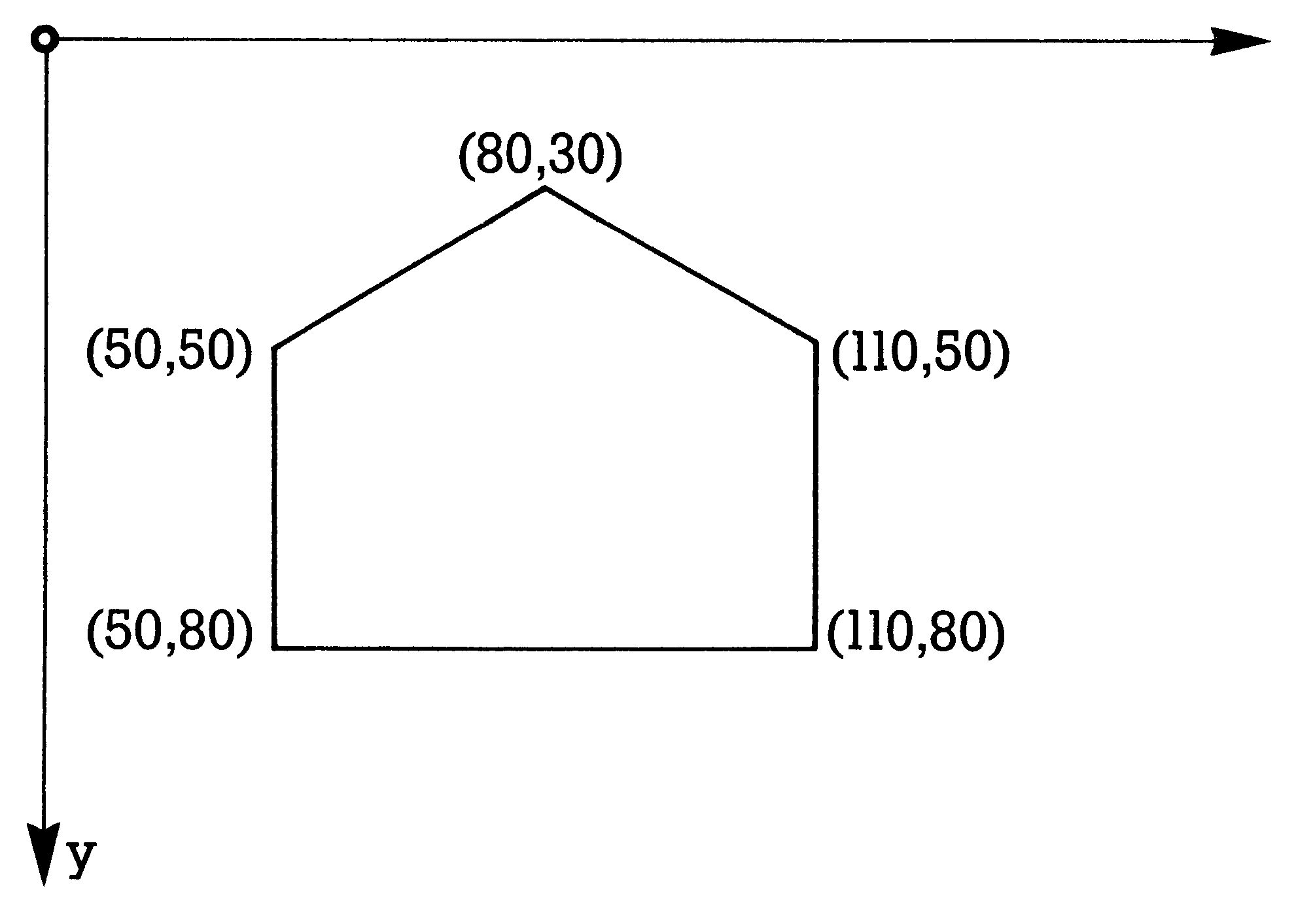
Dem CORE-System nachgebildet, würden die Befehle folgendermaßen lauten:
LOCATE 50,50
DRAW1 TO 50,80
DRAW1 TO 110,80
DRAW1 TO 110,50
DRAW1 ,30
DRAW1 TO 50,50
In unserer Grafiksprache müßten wir schreiben:
LINIE (50,50,50,80)
LINIE (50,80,110,80)
LINIE (110,80,110,50)
LINIE (110,50,80,30)
LINIE (80,30,50,50)
Schon in diesem Beispiel, wo die für das CORE-System günstigeren miteinander verbundenen Linien zu zeichnen sind, haben wir einen Befehl mehr zu verarbeiten. Ganz deutlich tritt der Unterschied zutage, wenn nicht verbundene Strecken zu zeichnen sind. Dann muß vor jeden DRAW-Befehl ein LOCATE treten, das den Cursor auf den Startpunkt einer Linie setzt. Das kostet die auf einem 8-Bit-Computer arbeitenden Grafiksysteme wertvolle Zeit.
Nebenbei sei noch bemerkt, daß das Basic 7.0 seinem DRAW-Befehl ein Zwitterdasein verliehen hat, wie Sie aus dem Vergleich der Übersetzung für den LINIE-Befehl und den CORE-Befehlen ersehen konnten. Das obige Programmproblem läßt sich beim C 128 sogar in einem Befehl erledigen:
DRAW 1,50,50 TO 50,80 TO 110,80 TO 110,50 TO 80,30 TO 50,50
Aus Gründen der Rechenzeiten, der besseren Überschaubarkeit eines Befehles und weil es einfach zu kompliziert wäre, HIRES-3 cursororientiert zu gestalten, wurde die cursorfreie Methode für unsere allgemeinen Grafikbefehle gewählt.
Noch mal etwas fürs Auge
Weil die Anwender des C 128 in den bisher vorgestellten gerätespezifischen Programmen zu kurz gekommen sind, sei ihnen als Trost das Listing 3 angeboten. Es erzeugt interessante Effekte durch Zeichnen ineinander verschachtelter, gegeneinander verdrehter Quadrate (siehe Bild 2).
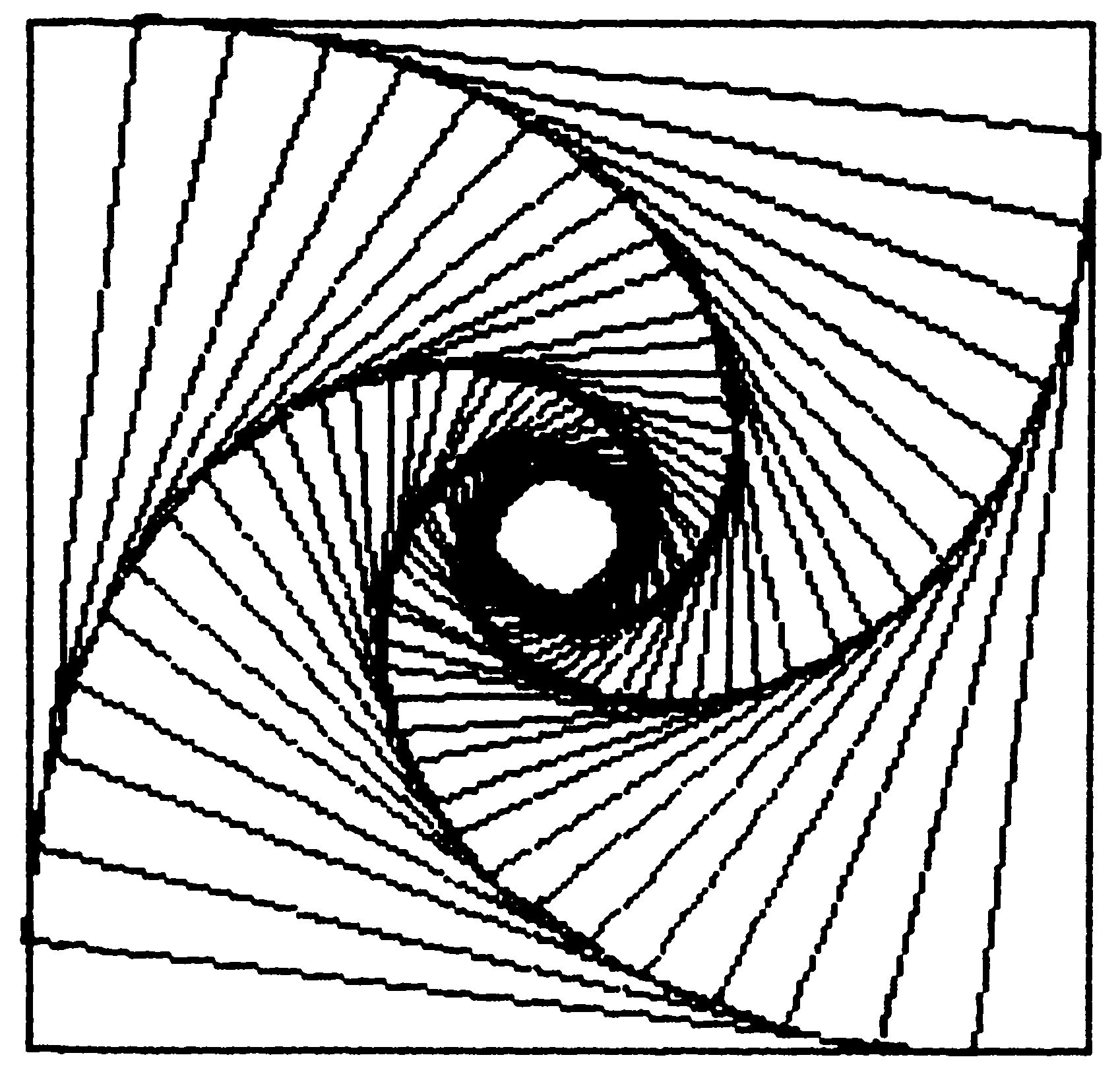
Frei wählbar ist die Größe, der Drehwinkel, die Anzahl und der Ort auf dem Bildschirm. Bei geschickter Programmierung können die Ergebnisse als sogenannte Shapes miteinander kombiniert werden.
Nulldimensional: der Punkt
Betrachten Sie bitte alles bisher Behandelte als Rüstzeug, das wir für unsere Streifzüge durch die Grafikwelt nunmehr angelegt haben. Unser Weg wird uns durch alle Dimensionen führen: Vom Punkt zur 4.Dimension, um diesen Titel vom berühmten Colerus zu entleihen. Und damit haben wir sie auch schon angesprochen: die vielgehaßte, aber auch vielgeliebte Mathematik. Denn professionelle Computergrafik ohne dieses Instrument ist nicht denkbar. Sie, die Sie Ihre letzte Begegnung mit dieser Wissenschaft irgendwann einmal in der Schule hatten, verzagen Sie bitte nicht! Was wir an Voraussetzungen brauchen, haben Sie in der 10.Klasse gelernt: Einfache Gleichungen mit einer oder mehreren Unbekannten zu lösen. Alles andere wird erklärt werden und das ohne trockenen, mathematischen Jargon.
Nach diesen Vorreden soll gleich der erste Begriff erklärt werden: die Dimension. Das Wort stammt aus dem Lateinischen und bedeutet Ausdehnung. So hat eine ebene Fläche davon zwei: Länge und Breite. Deshalb spricht man hier von zweidimensionalen Gebilden. Eine Linie hat nur ihre Länge als Ausdehnung, sie ist also eindimensional. Fassen wir zusammen:
| Dimension 0: | Punkt | – – – |
| Dimension 1: | Linie | Länge |
| Dimension 2: | Fläche | Länge, Breite |
| Dimension 3: | Körper | Länge, Breite, Höhe |
| Dimension 4: | ??? | Länge, Breite, Höhe, ??? |
In noch höhere Sphären werden wir uns nicht versteigen, obwohl manche Esoteriker der Ansicht sind, daß im Leben des Menschen sechs Dimensionen eine Rolle spielen.
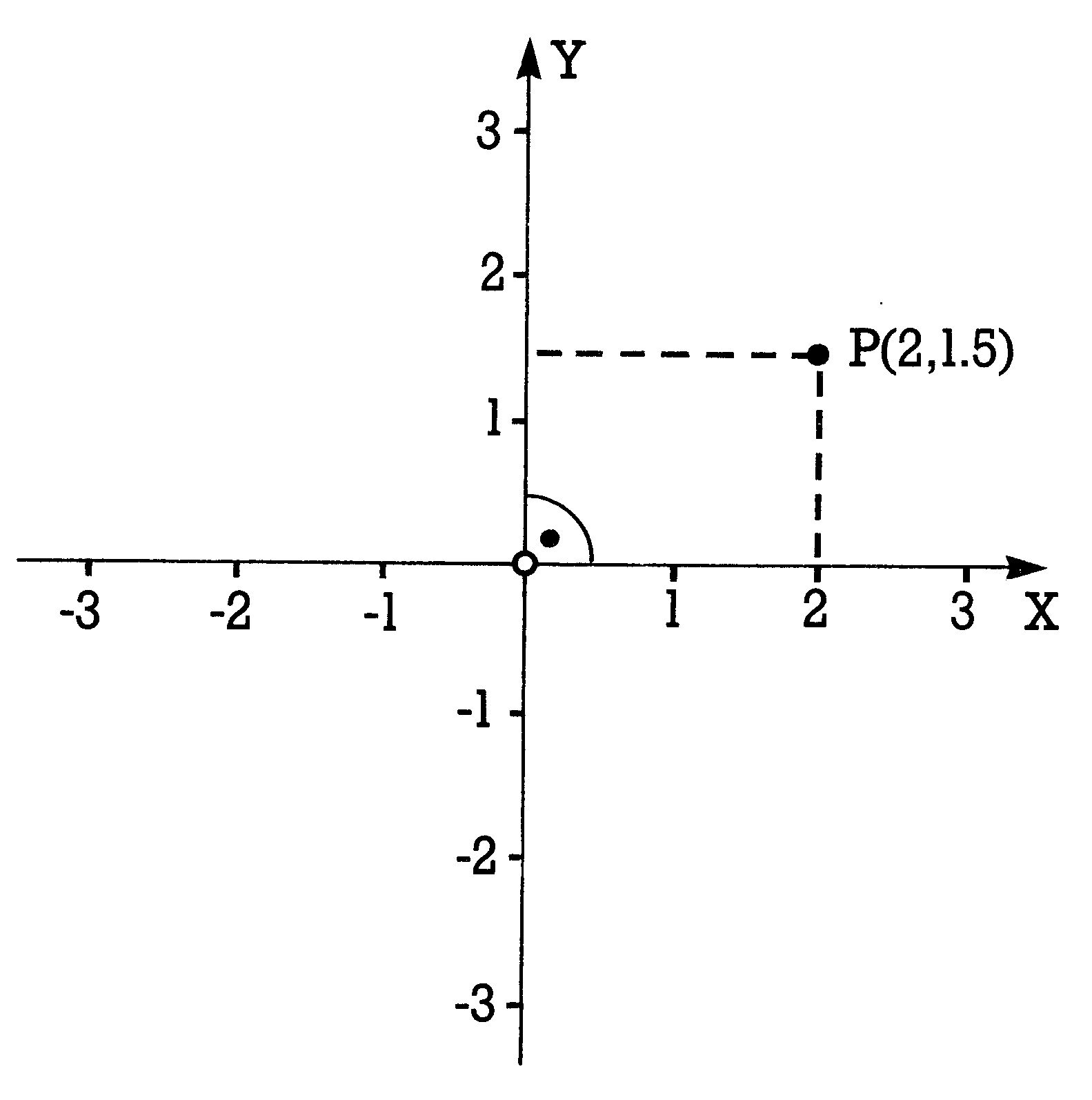
Beginnen wir also mit einem Gebilde der nullten Dimension, dem Punkt. Nun ist der Punkt an sich sicherlich ein wichtiges Thema für Philosophen, uns als Computergrafiker interessiert er aber immer in Verbindung irgendeiner Ortsbestimmung. Und weil wir — vor dem Bildschirm sitzend — eine Fläche vor uns haben, wollen wir auf dieser Fläche auch den Punkt sehen. Wie bestimmen wir, daß der Punkt an einem ganz bestimmten Ort auftauchen soll? Wir unterteilen unseren Bildschirm — der Computerhersteller hat das für uns schon erledigt — in einen Raster von 320 waagerechten und 200 senkrechten Positionen. Diese numerieren wir: Die horizontalen Positionen von links anfangend nach rechts und die vertikalen oben beginnend nach unten. Was sich auf diese Weise ergibt, nennt man ein Koordinatensystem (vom lateinischen »coordinare«, was »zuordnen« bedeutet). Jeder Punkt kann nun durch Angabe zweier Koordinaten in diesen Raster gelegt werden. Allgemein nennt man die der Waagerechten zugeordneten Zahlen X-Koordinaten und die anderen Y-Koordinaten. Ein Punkt wird dann häufig in der Form P(X,Y) charakterisiert. Beispielsweise liegt der Punkt P(160,100) genau in der Bildschirmmitte. Die Koordinatenachsen sind Linien, die durch den Punkt P0(0,0) laufen. Die X-Achse als Linie gesehen, enthält auf ihrer gesamten Länge nur Punkte mit der Y-Koordinate 0, umgekehrt ist es mit der Y-Achse, die überall den X-Wert 0 aufweist. Was sich auf diese Weise ergibt, ist das Koordinatensystem, wie es in Bild 3 gezeigt ist.
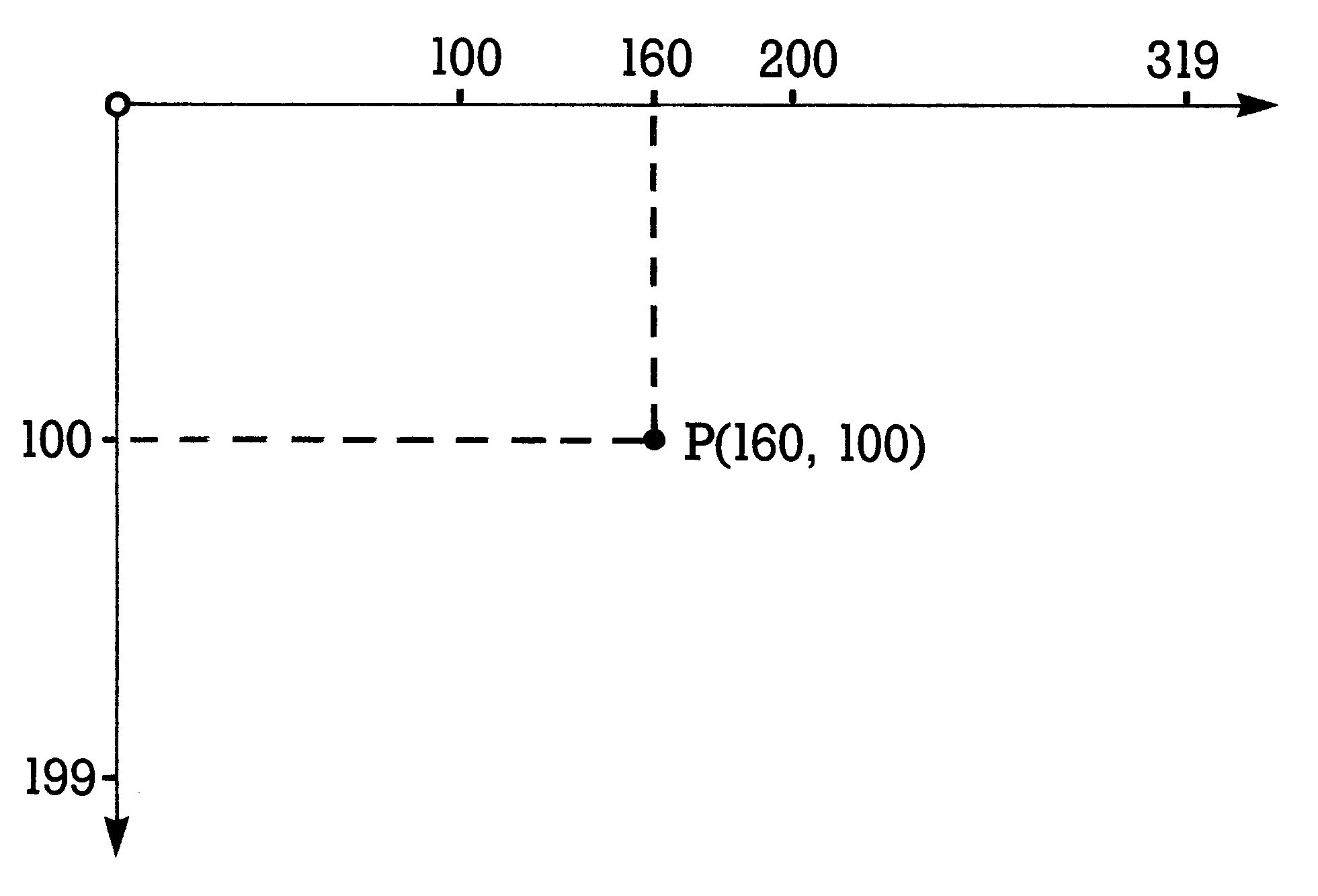
Koordinatensysteme
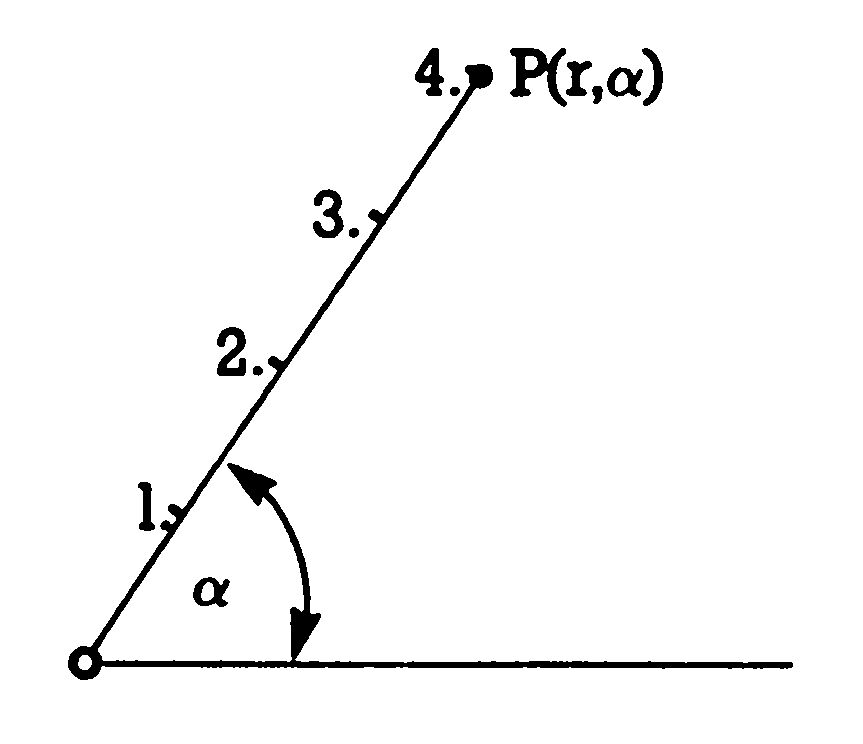
Den Ort von Punkten zu charakterisieren, ist im Prinzip noch auf vielerlei Weise möglich. So gibt es schiefwinklige Koordinatensysteme (siehe Bild 4) und manchmal verwendet man auch das sogenannte »polare« Koordinatensystem (siehe Bild 5). Hier werden die Länge des aus dem Ursprung kommenden Strahls und der Winkel, den dieser mit der Horizontalen bildet, zur Festlegung eines Ortes verwendet. Gebräuchlichstes Koordinatensystem allerdings ist das »kartesische«, angeblich benannt nach dem französischen Philosophen und Mathematiker Rene Descartes (von ihm stammt der berühmte Ausspruch »Ich denke, also bin ich«). Bild 6 zeigt ein kartesisches System, das durch die aufeinander senkrecht stehenden Achsen charakterisiert ist. Im allgemeinen verwendet man ein »rechtshändiges« System.
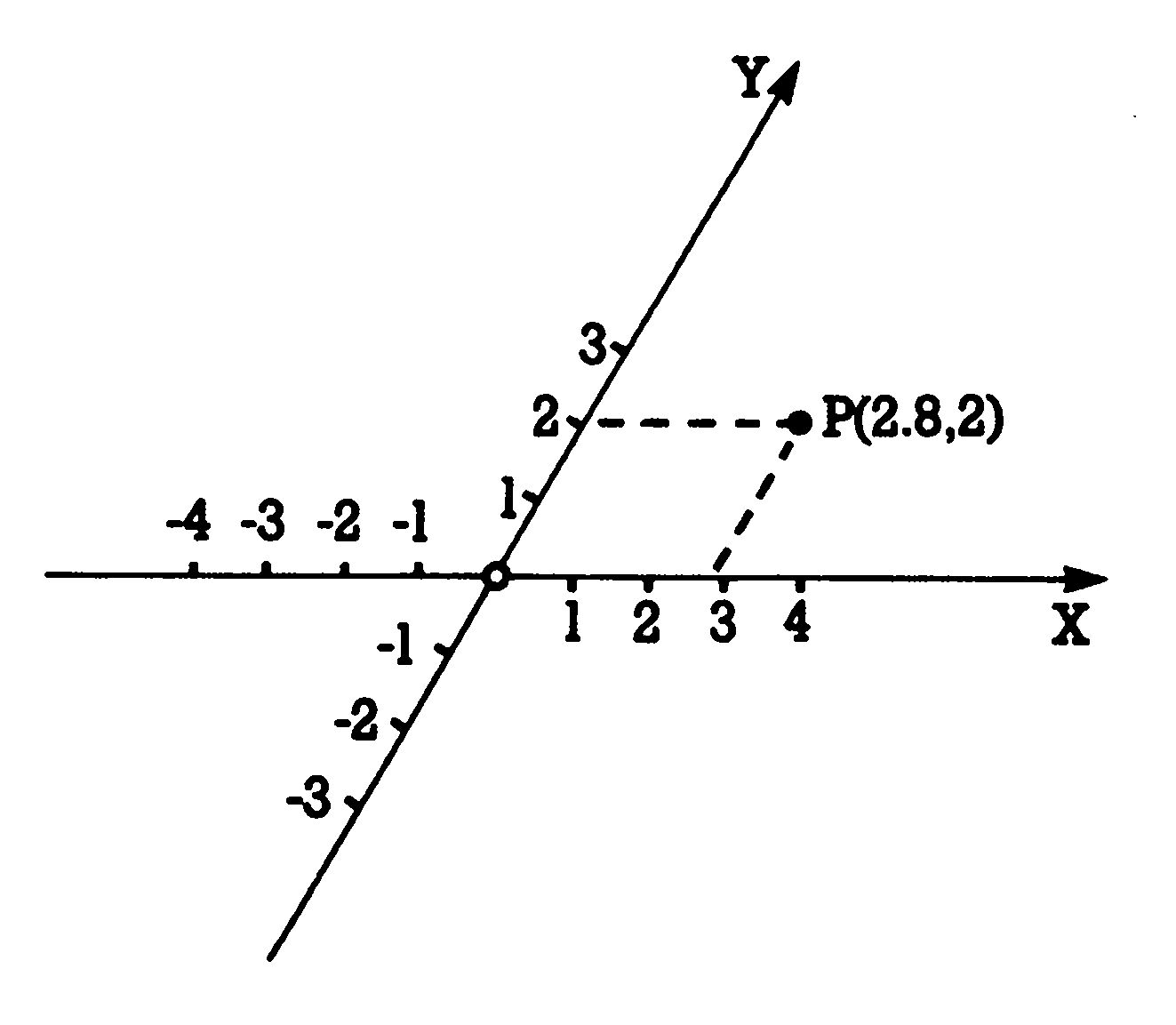
Transformationen
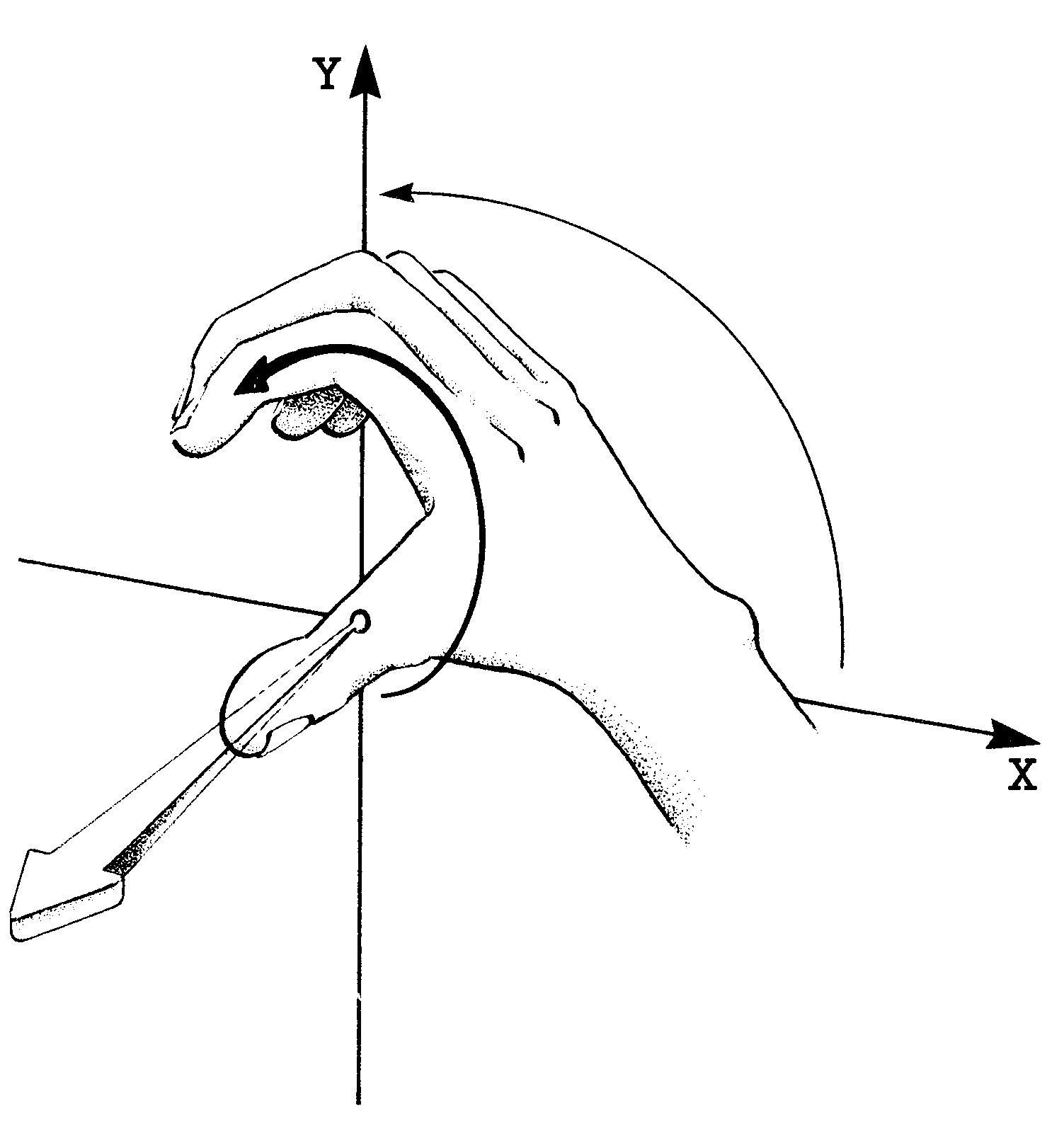
Rechtshängig deshalb, weil beim Drehen der X-Achse um den Ursprung (also um den Punkt P0(0,0)) diese auf dem kürzesten Wegzur Y-Achse die Richting einschlägt, in die die Finger der rechten Hand zeigen. Der Daumen weist dabei auf den Betrachter (siehe Bild 7).
Nun erkennen Sie vielleicht schon, daß Commodore uns ein reichlich ungebräuchliches Koordinatensystem beschert hat: Es ist nämlich linkshändig aufgebaut. Außerdem ist die Skala sowohl auf der X-, als auch auf der Y-Achse sehr unpraktisch, denn Punkte wie zum Beispiel P1(-1,4) oder P2(3,-5) und P3(-12,-3) können nicht gezeichnet werden, und ein Versuch, das trotzdem zu tun, endet mit einer Fehlermeldung.
Weiterhin sollten wir uns überlegen, daß Computergrafik für die verschiedensten Zwecke gebraucht wird: Ein Architekt will den Grundriß eines Hauses zeichnen, das in Richtung Norden 15 Meter und in Richtung Osten 18 Meter Ausdehnung besitzt. Ein Geschäftsmann möchte im Rahmen einer Kosten-/Nutzen-Analyse ein Diagramm erstellen, das Arbeitsaufwand in Stunden gegen produzierte Menge eines Artikels aufzeigt. Ein Ökologe zeichnet ein Schaubild, welches die zahlenmäßige Entwicklung der Weltbevölkerung in den letzten 50 Jahren darstellen soll. Kurz: Jeder von Ihnen benötigt ein anderes Koordinatensystem. Diese Art Koordinaten nennt man häufig die »Benutzerkoordinaten« und weil jeder Benutzer etwas aus einer 2D- oder 3D-Welt grafisch zeigen möchte, hat sich auch der Ausdruck »Weltkoordinaten« eingebürgert.
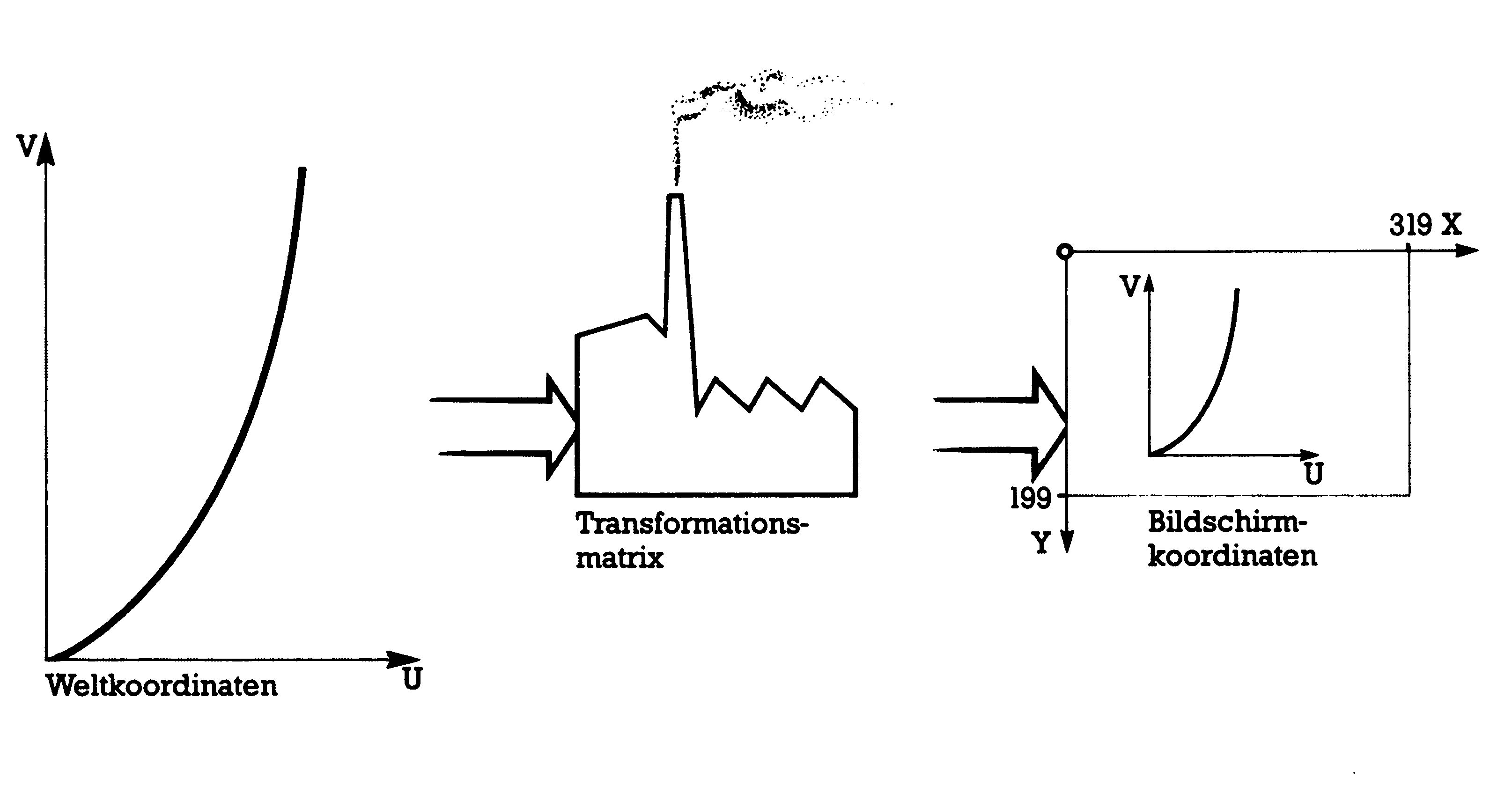
Wir müssen also irgendwie die Objekte der realen Welt, die wir im Weltkoordinatensystem festgelegt haben, auf unserem Bildschirm zeigen (siehe Bild 8). Weil es aber nicht möglich ist, auf dem Commodore-Bildschirm den Punkt P(1981,4508000) darzustellen (das ist beispielsweise die Aufgabe des oben erwähnten Ökologen), müssen wir irgendeine Form der Umrechnung durchführen. Solche Umrechnungen nennt man Transformationen (vom spätlateinischen »transformatio«, was Umbildung, Verwandlung von etwas bedeutet, ohne dessen Wert zu ändern).
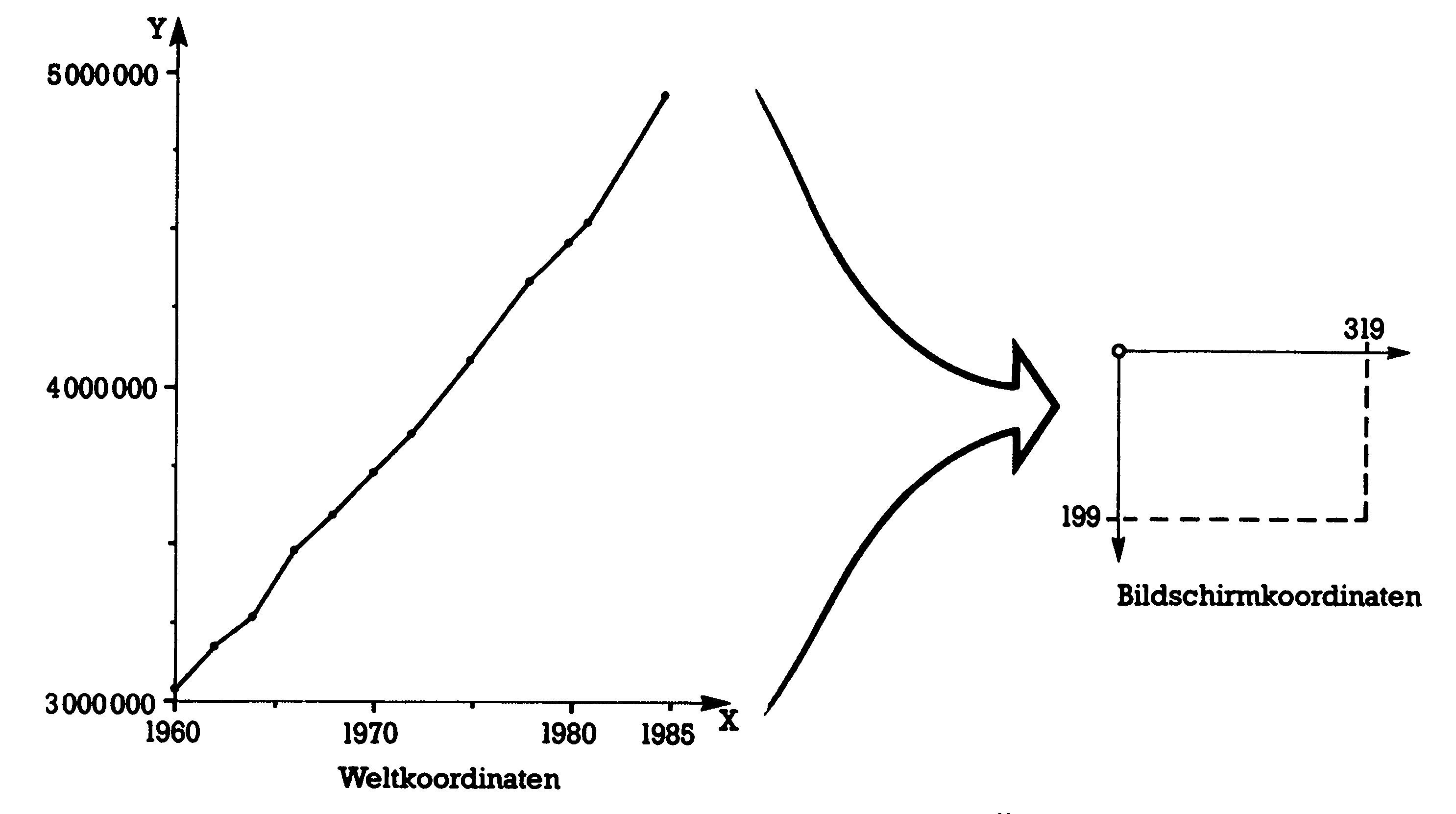
Nicht nur die Umrechnung der Weltkoordinaten in Bildschirmkoordinaten, sondern jede Veränderung eines Koordinatensystems kann durch Transformationen computergerecht durchgeführt werden. Wir werden dazu sogenannte Matrizenmathematik betreiben, deren Ergebnis dann die sogenannte Transformationsmatrix ist. Jeder Punkt des Weltkoordinatensystems wird gewissermaßen durch solch eine Transformationsmatrix hindurchgeschickt und kommt als Bildschirmpunkt wieder heraus (Bild 9). Transformationen können Vergrößerung oder Verkleinerung, Verschiebungen von Abbildungen oder ihre Drehung bewirken. Man kann damit Gebilde höherer Dimension auf solchen niedrigerer Dimension abbilden (wie sonst sollte man einen Würfel auf dem Bildschirm zeigen?) und umgekehrt. Es ist damit möglich, Objekte zu spiegeln, zu krümmen, stauchen oder zu zerren. Sie sehen schon, daß es sich lohnt, den Umgang mit Transformationsmatrizen kennenzulernen.
Unser Thema in der nächsten Folge werden also Matrizen sein und wie man Computer dazu bringen kann, uns die Hauptarbeit mit diesen merkwürdigen mathematischen Gebilden abzunehmen.
(Heimo Ponnath/tr)1000 rem *** up transformation ******** 1001 rem einmal zu definieren sind: 1002 rem xu,xo = niedrigster,hoechster 1003 rem x-wert 1004 rem yu,yo = niedrigster,hoechster 1005 rem y-wert 1006 rem fuer jeden punkt zu uebergeben 1007 rem x,y = punktkoordinaten aus 1008 rem beliebigen cartesischen 1009 rem koordinatensystem 1010 rem ausgegeben werden dann: 1011 rem xx,yy = bildschirmkoordinaten 1012 rem des 320/200-systems 1013 rem ****************************** 1020 xx=319*(x-xu)/(xo-xu) 1030 yy=199*(yo-y)/(yo-yu) 1040 return
1 rem ********************************* 2 rem * * 3 rem * fensterrose * 4 rem * version fuer den pc 128 * 5 rem * * 6 rem * heimo ponnath hamburg 1985 * 7 rem * * 8 rem ********************************* 9 rem ********* eingaben ********** 10 color0,1:color4,1:color5,6:scnclr 15 input"anzahl der stuetzpunkte";n 20 input"radius";r:input"textort xt,yt";xt,yt 25 rem ******** init ************** 30 color0,16:color1,7:color4,1:graphic1,1 35 rem ******** start/mitte ******* 40 xu=-160:xo=160:yu=-100:yo=100 55 rem **************************** 60 d=2*~/n:dimx(n),y(n) 65 rem ******** kreis ************* 70 x=0:y=0:gosub1020:x5=xx:y5=yy:rx=r*319/(xo-xu):ry=r*199/(yo-yu) 72 circle1,x5,y5,rx,ry 75 rem **************************** 80 gosub200 90 a$="fensterrose" 95 rem ******** text ************** 100 char1,xt,yt,a$ 105 rem ******* show(hier unnoetig) 115 rem *************************** 120 getkeyb$ 125 rem ******* normal ************ 130 graphic0:color0,1 135 rem ******* greset ************ 140 scnclr(1) 160 end 200 rem ******* up zeichnen ******* 210 fori=1ton:t=t+d:x(i)=r*cos(t):y(i)=r*sin(t):nexti 220 s=n-1 230 fori=1tos:z=i+1 240 forj=zton 242 rem ******* linie ************* 243 x=x(i):y=y(i):gosub1020:x1=xx:y1=yy:x=x(j):y=y(j):gosub1020:x2=xx:y2=yy 245 draw1,x1,y1tox2,y2 247 rem *************************** 250 nextj:nexti:return 1000 rem *** up transformation ******** 1020 xx=319*(x-xu)/(xo-xu) 1030 yy=199*(yo-y)/(yo-yu) 1040 return
1 rem ********************************* 2 rem * * 3 rem * verschlungene spiralen * 4 rem * version fuer den pc128 * 5 rem * * 6 rem * heimo ponnath hamburg 1985 * 7 rem * * 8 rem ********************************* 9 rem ******** eingaben ********** 10 color0,1:color4,1:color5,6:scnclr 15 input"anzahl spiralen";n:input"textstart xt,yt";xt,yt 20 input"radius,startwinkel";r,a 22 rem ******* init ************** 23 color0,16:color1,7:color4,1:graphic1,1 25 rem ******* start/mitte ******* 30 xu=-160:xo=160:yu=-100:yo=100 32 fast:gosub100 33 rem ******* kreis ************* 35 x=0:y=0:gosub1020:x5=xx:y5=yy:rx=r*319/(xo-xu):ry=r*199/(yo-yu) 37 slow:circle1,x5,y5,rx,ry 40 a$="verschlungene spiralen" 42 rem ******* text ************** 45 char1,xt,yt,a$ 50 rem ******* show (hier unnoetig) ** 55 getkeyb$ 60 rem ******* normal ************ 62 graphic0:color0,1 65 rem ******* greset ************ 67 scnclr(1) 70 end 100 rem ****** up zeichnen ******* 102 nn=n*100:ra=r/nn:dimt(nn) 105 forj=1ton:a=a+2*~/n 110 t=a:th=2*~/100:t(0)=t 115 fori=1tonn:t(i)=t(i-1)+th:rr=ra*i 117 x=(rr-ra)*cos(t(i-1)):y=(rr-ra)*sin(t(i-1)):gosub1020:xa=xx:ya=yy 119 x=rr*cos(t(i)):y=rr*sin(t(i)):gosub1020:xb=xx:yb=yy 120 draw1,xa,yatoxb,yb 125 nexti 130 nextj 135 return 1000 rem *** up transformation ******** 1001 rem einmal zu definieren sind: 1002 rem xu,xo = niedrigster,hoechster 1003 rem x-wert 1004 rem yu,yo = niedrigster,hoechster 1005 rem y-wert 1006 rem fuer jeden punkt zu uebergeben 1007 rem x,y = punktkoordinaten aus 1008 rem beliebigen cartesischen 1009 rem koordinatensystem 1010 rem ausgegeben werden dann: 1011 rem xx,yy = bildschirmkoordinaten 1012 rem des 320/200-systems 1013 rem ****************************** 1020 xx=319*(x-xu)/(xo-xu) 1030 yy=199*(yo-y)/(yo-yu) 1040 return
1 rem ********************************* 2 rem * * 3 rem * der box-befehl des pc 128 * 4 rem * * 5 rem * heimo ponnath hamburg 1985 * 6 rem * * 7 rem ********************************* 8 rem ********** eingaben *********** 9 color0,1:color4,1:color5,6:scnclr 10 input"groesste kantenlaenge";a 20 input"drehwinkel,anzahl";w,n:w1=w:w=w*~/180 30 input"zentrum x,y";x,y 40 dimx1(n),y1(n),x2(n),y2(n) 45 rem ********* 1. box ************* 50 d=(a/2)*(1-(1/(cos(w)+sin(w)))) 60 x1(0)=x-a/2:y1(0)=y-a/2:x2(0)=x+a/2:y2(0)=y+a/2 65 color0,2:color1,7:color4,1 70 graphic1,1 80 box1,x1(0),y1(0),x2(0),y2(0):i=0 85 rem ********* restliche boxen **** 90 do until i=n 95 i=i+1:d=d/(cos(w)+sin(w)) 100 x1(i)=x1(i-1)+d:y1(i)=y1(i-1)+d:x2(i)=x2(i-1)-d:y2(i)=y2(i-1)-d 105 if x2(i)-x1(i) <=0 then exit 110 box1,int(x1(i)),int(y1(i)),int(x2(i)),int(y2(i)),i*w1,0 120 loop 125 rem ******** ende *************** 130 getkeya$:graphic0 140 color0,1 150 end
