Netzwerkanalyse — Ein Programm für Hobby-Elektroniker
Dieses Programm simuliert und analysiert elektronische Schaltungen und ist daher ein Muß für jeden ambitionierten Hobby-Elektroniker.
NEWA2, wie das Programm im weiteren genannt wird, ist ein Netzwerkanalyseprogramm für den C 64 mit Diskettenlaufwerk und Simons Basic. Das Programm eignet sich zur Simulation und Analyse passiver und aktiver elektrischer Schaltungen. Es berechnet den Frequenzgang und den Phasenverlauf von Schaltungen, die aus Widerständen, Kondensatoren, Induktivitäten, Transistoren, Operationsverstärkern und allgemeinen Vierpolen bestehen. Das Programm kann somit zum Entwickeln von Verstärkerschaltungen, Filtern und Schaltungen der HF- und Funktechnik herangezogen werden. Neben der Berechnung kann der Frequenzgang durch ein »Bode-Diagramm« grafisch dargestellt werden. Dabei wird die Verstärkung, ausgedrückt durch das logarithmische Maß in dB, über dem logarithmischen Maß der Frequenz aufgetragen. Sowohl die Berechnungen wie aber auch das Bode-Diagramm können auf dem Drucker normiert, das heißt auf einen bestimmten Verstärkungsbetrag bezogen, ausgegeben werden. Zu beachten ist allerdings, daß der benutzte Drucker kompatibel zu den Commodore-Druckern ist beziehungsweise ein kompatibles Interface hat, da die Hardcopy über den Befehl COPY des Simons Basic ausgegeben wird. Die Schaltungsdaten und die Frequenzgänge lassen sich als sequentielles File auf Diskette abspeichern. Dadurch wird die Möglichkeit gegeben, Schaltungen zu einem späteren Zeitpunkt nochmals mit geänderten Werten zu bearbeiten. Die Theorie zu diesem Programm ist zwar nicht leicht zu verstehen, wird aber im folgenden ausführlich behandelt. Anhand von zwei Beispielen, die einen aktiven Bandpaß und einen aktiven Klangregler behandeln, wird versucht, dem Leser dieses Thema näher zu bringen. Wer sich intensiver mit dem Entwurf von Schaltungen beschäftigen möchte, dem sei angeraten, sich das Buch zu diesem Thema »Halbleiter Schaltungstechnik« von U. Tietze und Ch. Schenk, erschienen im Springer-Verlag, zu besorgen.
Die gesamte Bedienung des Programms erfolgt in Menütechnik und ist daher sehr einfach. Fehler werden soweit wie möglich vom Programm abgefangen. Das Eintippen dieses 10 KByte langen Programms ist zwar ein Stückchen Arbeit, aber dafür erspart es jedem ambitionierten Elektronikbastler Stunden des Probierens und Tüftelns beim Schaltungsentwurf.
(Hans Haberl/ah)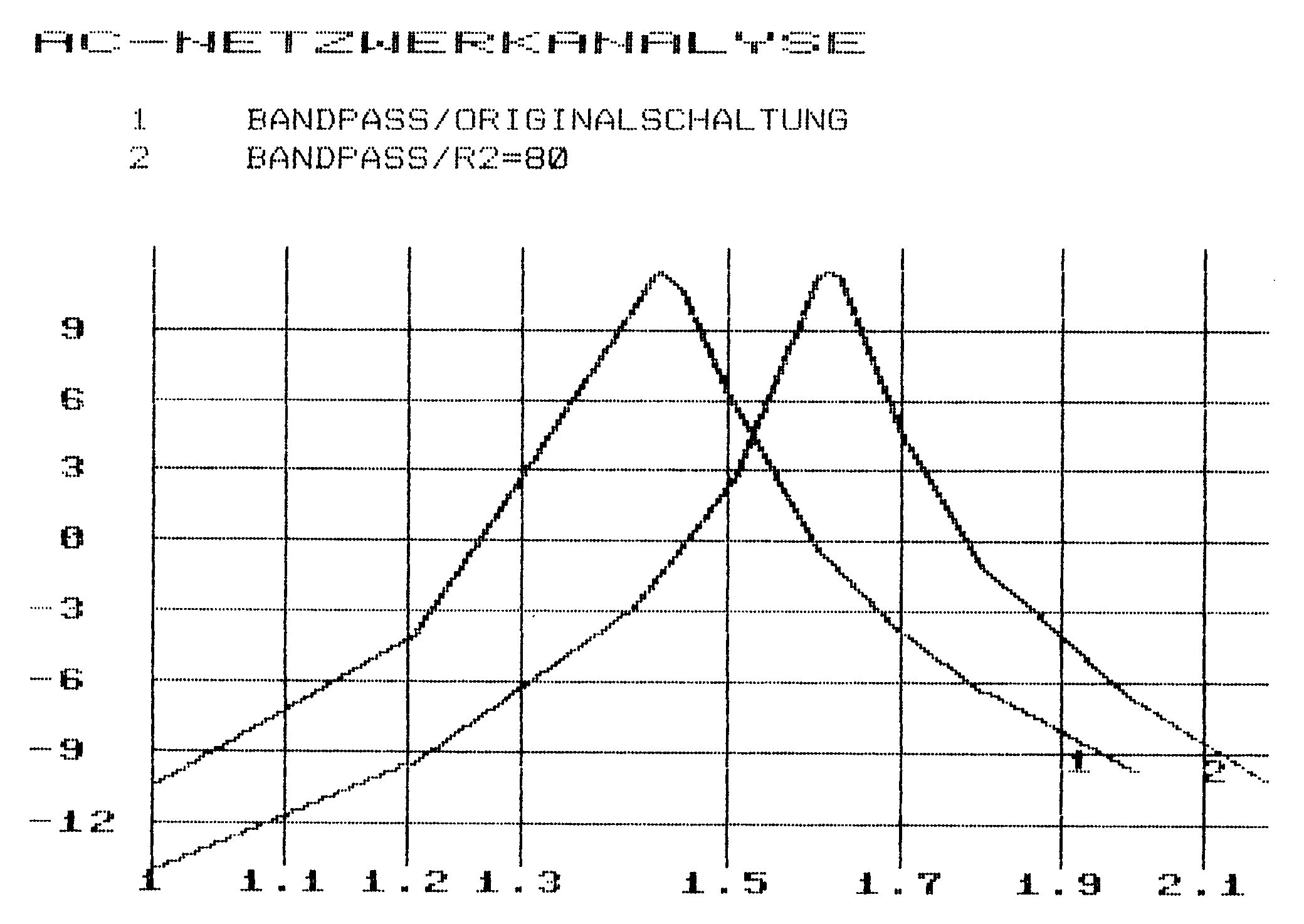
Durch dieses Programm erspart sich jeder Elektronik-Bastler Stunden des Probierens und Tüftelns beim Entwurf frequenzkritischer Schaltungen.
Das Programm ist in Simons Basic geschrieben. Sie müssen also zuerst diese Erweiterung laden, bevor Sie »NEWEA2« (Listing 1) eintippen.
Wenn Sie damit fertig sind, wollen wir gleich voll einsteigen und die Bedienung anhand eines Beispiels erklären.
Nach dem Initialisieren meldet sich NEWEA2 mit dem Hauptmenü. Darunter blinkt ein gelber Cursor, was heißt, daß die angeforderte Eingabe nur aus einem Zeichen besteht und nicht mit RETURN abgeschlossen werden muß. Bei einem grauen Cursor dagegen muß die Eingabe mit RETURN abgeschlossen werden, Sie können auch nur ein RETURN eingeben, wenn der alte Wert vor dem Fragezeichen steht und übernommen werden soll. Werden mehrere Eingaben auf einmal angefordert, so müssen diese durch Kommata getrennt werden.
Ein Beispiel
Netzwerkeingabe
Geben Sie nun »N« für Netzwerkeingabe ein. Wir wollen nämlich den in Bild 1 gezeigten aktiven Bandpaß als erstes Beispiel analysieren. Das Programm fragt nun nach der Anzahl der Knoten. Ein Knoten ist jedes zugängliche Potential in einer Schaltung, also die Punkte, die Sie auch mit einem Meßgerät erreichen können. Da der Masseknoten nicht mitgezählt wird, sind es in unserem Beispiel vier Knoten. Der Knoten zwischen Quelle U0 und Quellwiderstand R0 zählt ebenfalls nicht, da er nicht zur untersuchten Schaltung gehört. Nun geben Sie auf die Fragen des Programms die Anzahlen der Elemente ein: drei Widerstände, zwei Kondensatoren und ein Operationsverstärker, sonst überall 0.
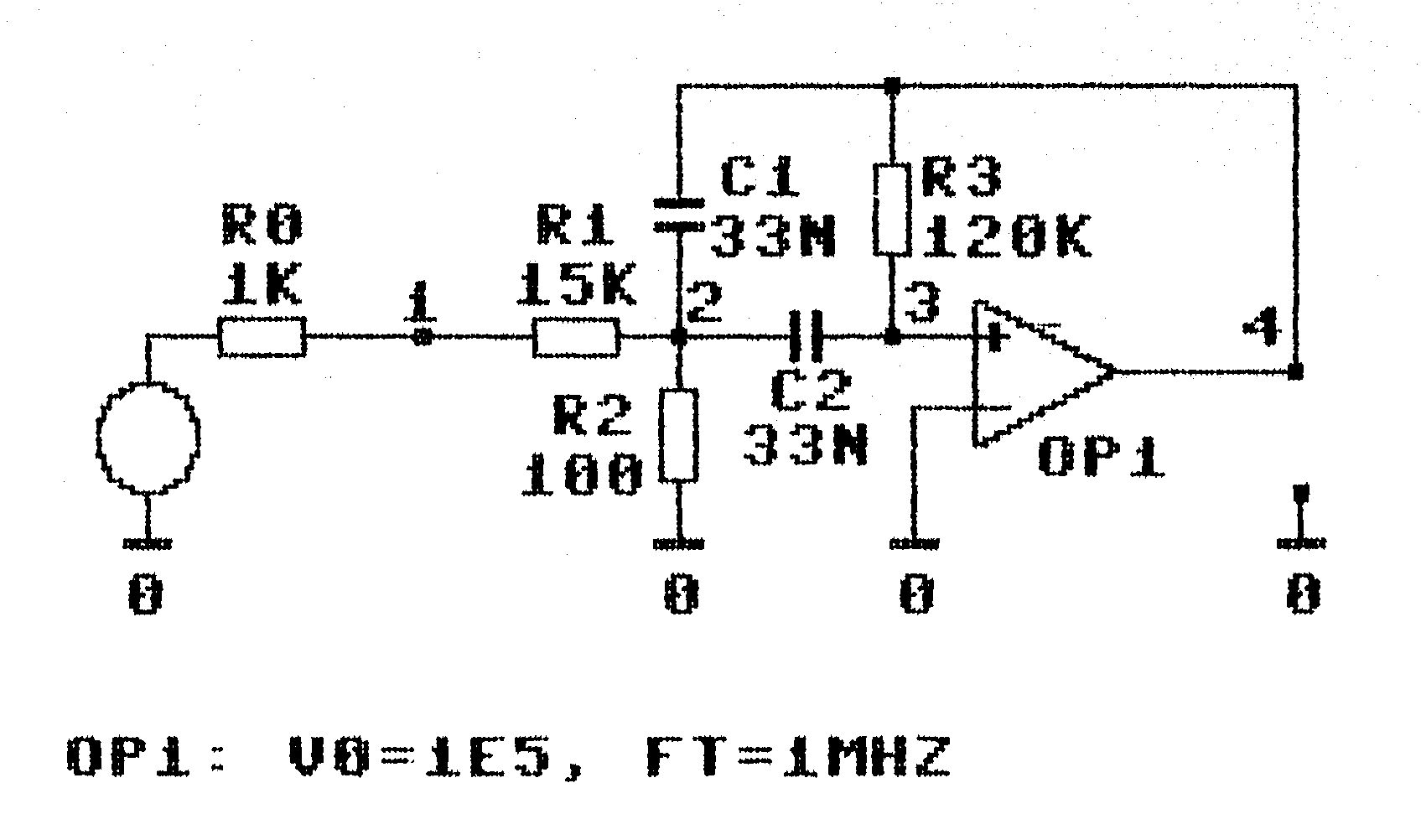
| WIDERSTÄNDE R | |
| R 0 ( 0 1 ) | 1000 |
| R 1 ( 1 2 ) | 15000 |
| R 2 ( 2 0 ) | 100 |
| R 3 ( 3 4 ) | 120000 |
| KAPAZITÄTEN C | |
| C 1 ( 2 4 ) | 3.3E-08 |
| C 2 ( 2 3 ) | 3.3E-08 |
| OPs + - A | |
| OP 1 ( 3 0 4 ) VO,FT | 100000 1000000 |
| AUSGANGSKNOTEN | 4 |
Nun kommt — wie immer nach einem Block von Eingaben — die Frage »Korrektur?« Geben Sie hier ein »J« für Ja, so können Sie diesen Eingabeblock wiederholen, um eventuelle Fehleingaben zu korrigieren. Bei jedem anderen Zeichen fährt das Programm normal fort. Apropos Fehleingaben: Unerlaubte Eingaben werden fast alle erkannt und durch Wiederholen der Frage oder des ganzen Blocks quittiert. »Fast« sage ich deshalb, weil es auch »intelligente« Fehleingaben gibt, die das Programm nicht sofort erkennt, wie zum Beispiel ein Knoten, an dem kein Element liegt, ein Kurzschluß am Ausgang oder galvanisch getrennte Teilschaltungen (die Schaltung muß zusammenhängen, da NEWEA2 ein gemeinsames Bezugspotential benötigt). Solche Fehler werden erst bei der Berechnung erkannt.
Nun möchte das Programm wissen, an welchen Knoten die Elemente anliegen. Bei der Numerierung der Knoten müssen Sie zwei Dinge beachten:
- Der Masseknoten besitzt die Nummer 0.
- Der Eingangsknoten besitzt die Nummer 1. An diesen Knoten legt das Programm automatisch die Eingangsspannungsquelle, Sie müssen diese also nicht explizit angeben.
Die Numerierung der übrigen Knoten sowie der Bauelemente (außer R0) ist beliebig. Somit dürfte die Eingabe des Netzwerkes kein Problem mehr sein. Außerdem können Sie im Beispielausdruck sehen, wie es geht. Bei mehr als zweipoligen Elementen wird die Reihenfolge der Knoten — CBE beim Transistor und ±A beim Operationsverstärker — mit angezeigt. Der zuletzt erfragte Knoten — der Ausgangsknoten — ist derjenige Knoten, dessen Potential als Ausgangsspannung betrachtet wird. Das muß nicht unbedingt der tatsächliche Ausgang der Schaltung sein, sondern Sie können sich beliebige Spannungen innerhalb der Schaltung ansehen. In unserem Beispiel interessiert uns jedoch der richtige Ausgang, also Knoten 4.
Als nächstes müssen wir die Elementewerte eingeben, und zwar in Grundeinheiten, also Ohm, Farad, Henry, Hertz, Ampere etc. Beim Operationsverstärker wird noch genauer formuliert, was eingegeben werden soll: die Leerlaufspannungsverstärkung V0 und die Transitfrequenz FT, hier mit 100000 beziehungsweise 1 MHz angenommen.
Dann rechnet das Programm zum ersten Mal, es stellt nämlich die sogenannte Knotenleitwertmatrix Yn sowie die Strukturmatrix auf. Während das Programm arbeitet, ist es nicht ansprechbar und macht dies durch das Wörtchen »busy« klar. Danach können Sie das Netzwerk noch auf den Drucker ausgeben lassen. Sollten Sie hier ein »J« getippt haben, der Drucker aber gerade nicht gewillt sein zu drucken, so bricht das Programm zwar mit einem »Device not present« ab, kann aber durch Drücken der F1-Taste ohne Datenverlust fortgesetzt werden.
Frequenzgangberechnung
Jetzt sind wir wieder im Hauptmenü und geben »F« für Frequenzgangberechnung ein. Nun müssen wir ein »Frequenzfile« angeben, in dem wir den Frequenzgang speichern wollen. Diese Nummer darf zwischen 1 und 9 liegen und dient dazu, später wieder Bezug auf diesen Frequenzgang nehmen zu können, zum Beispiel um ihn grafisch darzustellen oder auf Diskette zu speichern. Geben Sie hier eine 0 ein, so kehrt das Programm ins Hauptmenü zurück. Wie Sie später sehen werden, dient die 0 oft dazu, eine Eingabe abzubrechen. Zusätzlich zur Nummer können Sie nun noch eine Notiz eingeben, die später immer zusammen mit der Nummer angezeigt wird. Man braucht sich also nicht zu merken, welche Nummer ein bestimmter Frequenzgang hat. In unserem Beispiel könnte die Notiz zum Beispiel lauten:
»Bandpaß, Originalschaltung« (Wenn der Text Kommata oder Doppelpunkte enthält, muß er in Anführungszeichen gesetzt werden. Das gleiche gilt beim Speichern, wenn Sie einem Filenamen einen Klammeraffen vorausstellen, um ein bereits existierendes File zu überschreiben).
Jetzt wird's ernst: Geben Sie nun die erste Frequenz (im Bereich zwischen 1 000 und 2 000 Hz) ein! Der Bandpaß hat seine Resonanzfrequenz im Bereich zwischen 1 und 2 kHz. Suchen Sie diese doch einmal, ohne im Beispielausdruck nachzuschauen. In ein Frequenzgangfile passen maximal 20 Frequenzen. Wollen Sie die Eingabe schon früher abbrechen, so geben Sie eine 0 ein. Hier gleich noch ein Tip zum Suchen von Resonanzfrequenzen: Schauen Sie nicht nur auf den Betrag, sondern auch auf die Phase. Bei Resonanzfrequenzen ist dies meist ein ganzzahliges Vielfaches von 90 Grad, in unserem Beispiel 180 Grad.
Nach Abbruch der Frequenzgangberechnung stellt das Programm die Frage, ob Sie das File mit einem anderen vergleichen wollen (#), ob Sie es normieren (N) oder auf den Drucker (D) ausgeben wollen. Drücken Sie hier erst mal eine beliebige andere Taste (zum Beispiel RETURN oder Space), um ins Hauptmenü zurückzukommen. Da Sie die Frequenzen beim Suchen des Maximums bestimmt durcheinander eingegeben haben, wollen wir jetzt in Ruhe den sortierten Frequenzgang betrachten: Geben Sie »A« ein und dann die Nummer, die Sie für Ihr Frequenzfile gewählt haben. Die Frage »Notiz« beantworten Sie mit RETURN, damit die alte Notiz übernommen wird. Jetzt wird der ganze Frequenzgang fein säuberlich sortiert ausgegeben.
Nun wollen wir an unserer Schaltung ein bißchen »herumbiegen« und sehen, was passiert. Drücken Sie dazu erst wieder eine Taste, um ins Hauptmenü zu kommen und dann ein »E« für Elementeingabe. Dadurch sparen wir uns das ganze »Durchtippen« der Netzwerkeingabe und kommen gleich zu dem Eingabeblock für die Elementwerte. Ändern Sie den Wert für R2 von 100 nach 80 Ohm und lassen Sie die übrigen Werte gleich. Wählen Sie dann wieder den Menüpunkt »F« an und geben eine neue Frequenzfilenummer an, zum Beispiel die 2, wenn Sie vorher die 1 belegt hatten. Damit wir nun nicht alle Frequenzen noch einmal eintippen müssen, bietet uns das Programm die Möglichkeit, Frequenzen von einem bereits belegten Frequenzfile zu übernehmen. Geben Sie dazu auf diese Frage die Nummer Ihres ersten Files, also zum Beispiel 1 ein. Wenn Sie auf die nächste Frage nun ein »J« geben, dann wird der neue Frequenzgang ohne Zwischenfragen mit den Frequenzen des alten Files berechnet, geben Sie dagegen kein »N« so fragt das Programm bei jeder Frequenz nach und Sie können diese durch RETURN übernehmen oder aber durch eine andere ersetzen. Probieren Sie es erst einmal mit »J«. Sie werden dann jedoch feststellen, daß sich das Maximum verschoben hat und dort, wo es vorher war, sich jetzt viele unnütze Frequenzen herumräkeln, während das neue Maximum nicht genau erfaßt ist. Wir wollen deshalb einen zweiten Versuch machen: Geben Sie vom Hauptmenü aus wieder »F« ein und anschließend wieder Filenummer 2. Auf die Frage »Frequenzen von File« brauchen Sie diesmal nur mit RETURN zu antworten, da die Frequenzen von File 1 ja schon vorher in File 2 kopiert wurden. Auf die Frage »Ohne Änderung« geben Sie jedoch diesmal ein »N«. Das Programm hält nun bei jeder Frequenz an und Sie können diese durch RETURN übernehmen oder eine andere eingeben.
Wenn Sie die Frequenzgangberechnung abgeschlossen haben, gehen Sie nicht gleich ins Hauptmenü zurück, sondern geben Sie auf die Frage »File #, Normierung oder Drucker« die Nummer Ihres ersten Files, also 1 ein. Das zuletzt berechnete File wird nun mit File 1 verglichen, wobei nur gleiche Frequenzen nebeneinanderstehen. Außerdem erfolgt die Ausgabe nur solange, wie sich die Files überdecken. Nun können Sie gleich noch den Punkt »Normierung« ausprobieren. Damit können Sie den Frequenzgang bei einer bestimmten Bezugsfrequenz auf einen bestimmten dB-Wert normieren, also zum Beispiel 0 dB bei der Resonanzfrequenz (die Bezugsfrequenz muß also im Frequenzgang enthalten sein).
Frequenzgangdiagramm
Da die Zahlenreihen für Frequenzgänge nicht unbedingt anschaulich sind, kann NEWEA2 das ganze auch grafisch: Geben Sie dazu »D« vom Hauptmenü aus. Da mehrere Frequenzgänge in einem Diagramm dargestellt werden können, fragt das Programm hier nach den Nummern für das 1. (zu zeichnende) File, das 2. und so weiter. Wenn Sie nicht alle belegten Files auf einmal zeichnen wollen, können Sie auch hier die Eingabe durch eine 0 beenden. Zum Diagramm selbst: Auf der Y-Achse sind die dB-Werte aufgetragen, auf der X-Achse in logarithmischem Maßstab die Frequenz in Hz, KHz oder MHz. Diese scheinbar inkonsequente Benennung wurde gewählt, um zu lange Zahlen zu vermeiden. Durch Drücken einer beliebigen Taste kommen Sie wieder in den Normalmodus zurück und können dort durch ein »J« auf die nächste Frage das Diagramm ausdrucken lassen. Dazu brauchen Sie allerdings einen Commodore-Drucker VC 1515, VC 1525, MPS 801 oder einen anderen (zum Beispiel Epson) mit Commodore-kompatiblem Interface, da hier der COPY-Befehl des Simons Basic benutzt wird. Für andere Drucker können Sie jedoch das Programm anpassen, was sehr leicht ist, da alle Druckerbefehle in den Zeilen ab Nummer 7000 zusammengefaßt sind.
Speichern und Laden von Daten
Sowohl die Schaltungsdaten als auch die Frequenzfiles können auf Diskette gespeichert werden. Dazu wählen Sie im Hauptmenü den Punkt »S«. Danach geben Sie auf die Fragen »Schaltung speichern« beziehungsweise »Frequenzfiles speichern« je nach Bedarf ein »J« oder ein anderes Zeichen ein. Bei der Eingabe des Filenamens haben Sie durch Eingabe von »$« die Möglichkeit, sich alle sequentiellen Files auf einer Diskette anzeigenzu lassen. Beim Filenamen empfehle ich Ihnen, Schaltungs- und Frequenzgangfiles entsprechend zu markieren, zum Beispiel durch ein vorangestelltes S/.. beziehungsweise F/… Die Schaltungsdaten können Sie durch eine Notiz ergänzen, die beim Laden wieder ausgegeben wird, bei den Frequenzfiles wird natürlich die vorher eingegebene Notiz mit abgespeichert. Die Eingabe der Frequenzfilenummern geschieht genau so wie beim Diagramm, also am Ende der Eingabe durch 0.
Zum Laden ist noch folgendes zu sagen. Da im Speicher nur immer eine Schaltung Platz hat, wird beim Laden einer neuen Schaltung die alte gelöscht. Ganz anders dagegen bei den Frequenzfiles: Hier werden die Files von Diskette nur in noch freie Frequenzfiles geladen. Das hat folgende Konsequenzen:
- Es gehen grundsätzlich keine im Computer gespeicherten Daten verloren.
- Frequenzfiles haben beim Laden in der Regel nicht die selben Nummern wie beim Speichern. Identifizieren kann man sie ja anhand der Notizen.
- Wenn nicht genug freie Files im Computer vorhanden sind, werden nur so viele Files geladen, wie noch Platz ist. Dies wird durch eine Meldung beim Laden (zum Beispiel »nur 2 von 3«) mitgeteilt. Um im Computer Platz zu schaffen, muß man daher eventuell Files löschen. Dies geschieht ganz einfach durch Anwählen von »F« und der zu löschenden Filenummer und der Eingabe »0« als erste Frequenz.
Zur Theorie
Wenn Sie mit dem Programm »gespielt« haben und den Umgang damit beherrschen, dann wird es Zeit für die Theorie. Keine Angst, ich will Ihnen hier nicht die Grundlagen der Netzwerksynthese beibringen, aber einige Punkte müssen Sie zur Arbeit mit dem Programm wissen.
Lineare Schaltungen
Vielleicht haben Sie sich schon gefragt, warum bei den Elementen keine Dioden vorhanden sind. Der Grund dafür ist, daß NEWEA2 nur lineare Schaltungen untersuchen kann, das heißt der Zusammenhang von Strom und Spannung an jedem Element der Schaltung muß von der Form U = I x Konst, sein. Der Wert eines Widerstandes zum Beispiel muß immer gleich sein, ob an diesem Widerstand nun 1 V oder 10 V anliegen. Bei der Diode ist das aber nicht der Fall, ihr Widerstand ist abhängig von der anliegenden Spannung. Natürlich gibt es Programme, die auch nichtlineare Schaltungen untersuchen können, das sind sogenannte Transientenanalyse-Programme. Jedoch ist der Rechenaufwand dafür für den C 64 zu groß.
Wir müssen uns also auf lineare Schaltungen beschränken. Aber Transistor und Operationsverstärker sind auch nichtlineare Elemente! Wir können sie aber dennoch verwenden, wenn wir darauf achten, daß diese Elemente in den zu untersuchenden Schaltungen im linearen Bereich betrieben werden, denn das Programm sieht diese Elemente grundsätzlich als linear an.
Beim Operationsverstärker heißt das, daß die Ausgangsspannung, die durch die Versorgungsspannung gesetzten Grenzen nicht überschreiten darf, beim Transistor wird vorausgesetzt, daß dieser in einem vernünftig gewählten Arbeitspunkt betrieben wird. Natürlich gibt es auch Schaltungen, die die nichtlinearen Eigenschaften dieser Bauelemente ausnutzen, zum Beispiel Transistor als Schalter oder als Komparator. Solche Schaltungen können mit NEWEA2 nicht untersucht werden. Die Diode könnte man auch in einem Arbeitspunkt linearisieren und dann als normalen Widerstand darstellen. In der Praxis werden jedoch fast immer die nichtlinearen Eigenschaften einer Diode ausgenutzt, weshalb diese Darstellung kaum vorkommen wird.
Das Ersatzschaltbild (ESB)
Als Grundelemente zum Aufbau der zu untersuchenden Schaltungen stehen nur Widerstände, Kapazitäten, Induktivitäten sowie konstante und gesteuerte Strom- und Spannungsquellen zur Verfügung. Andere Elemente müssen aus diesen Elementen in bestimmten Anordnungen — den sogenannten Ersatzschaltungen — aufgebaut werden. Das einfachste Ersatzschaltbild ist das einer Spule: Da eine Spule eben nicht nur eine Induktivität, sondern auch einen ohmschen Widerstand besitzt, sollte sie — vor allem bei HF-Anwendungen — als Serienschaltung einer Induktivität und eines Widerstandes eingegeben werden. Der Widerstand hat dabei den Wert: \[R = \frac{2 \pi f L}{Q}\] wobei Q die Güte der Spule ist und f die Frequenz, bei der diese Güte gemessen wurde. Theoretisch besitzt die Spule auch noch eine Kapazität, ja sogar ein Widerstand hat Kapazitäten und Induktivitäten (Anschlußdrähte!), jedoch sind diese Effekte vernachlässigbar. Lediglich bei extremen HF-Anwendungen haben diese »parasitären« Elemente spürbare Einflüsse. Wenn man jedoch in solchen Frequenzbereichen arbeitet, kann man Schaltungssimulationen und Berechnungen sowieso vergessen, da hilft nur noch eins: Basteln.
Weitere Ersatzschaltbilder können natürlich beliebig eingegeben werden, diejenigen für Transistor und Operationsverstärker sind im Programm bereits vorhanden und werden in den nächsten Abschnitten noch besprochen.
Der Transistor
Das Ersatzschaltbild für den Transistor ist in Bild 2 zu sehen. Es ist ein Pi-Ersatzschaltbild mit fünf Elementen und in dieser Form im Programm bereits gespeichert. Es müssen lediglich drei Daten eingegeben werden:
- IC: Kollektorstrom im Arbeitspunkt.
- BO: Kurzschlußstromverstärkung (zirka 20….300).
- FT: Transitfrequenz (einige MHz bis GHz).
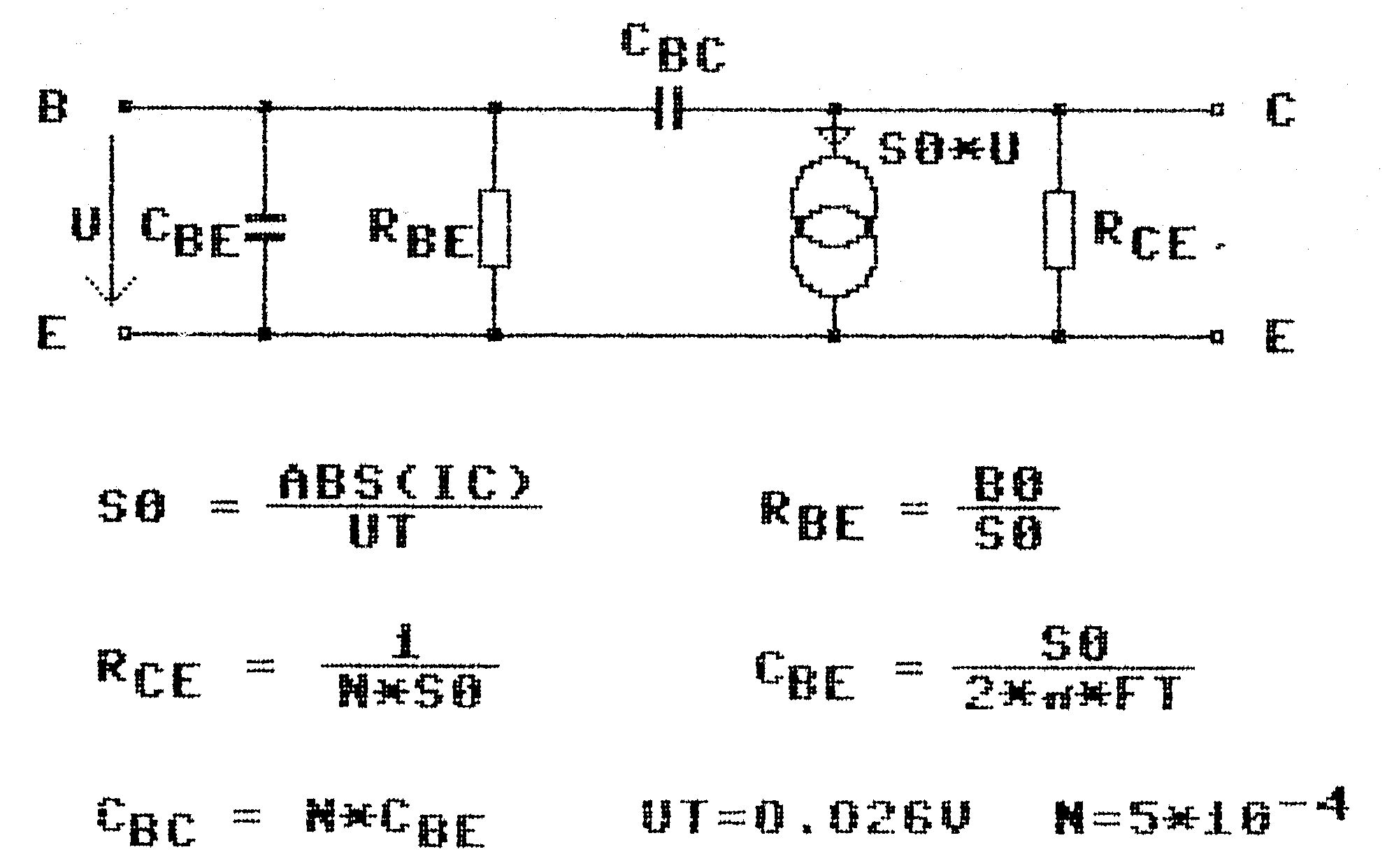
Die thermische Spannung Ut sowie der Basisweitenmodulationsfaktor n (eta) werden vom Programm mit 26 mV beziehungsweise 5 x 10-4 angenommen. Sollten diese Werte einmal nicht zutreffen, so kann der Transistor als Vierpol eingegeben werden. Natürlich kann auch das angegebene Transistor-Ersatzschaltbild erweitert werden. Sinnvoll ist allerdings nur, den Basisbahnwiderstand als Vorwiderstand in die Basisleitung zu schalten. Der hat zwar nur zirka 10 bis 100 Ohm, bildet aber einen frequenzabhängigen Spannungsteiler mit CBE. Er ist jedoch nur bei HF-Anwendungen und niederohmiger Ansteuerung des Transistors (oder Basisschaltung) sinnvoll.
Wie schon in einem früheren Abschnitt gesagt, muß der Transistor in einem sinnvoll gewählten Arbeitspunkt betrieben werden. Charakterisiert ist dieser Punkt durch den Kollektorstrom. In einem der noch folgenden Beispiele werden Sie sehen, daß die Eingabe dieser Werte jedoch meist recht unkritisch ist.
Der Operationsverstärker
Der Operationsverstärker ist im Programm als spannungsgesteuerte Spannungsquelle mit frequenzabhängiger Verstärkung V dargestellt. Ersatzschaltbild und die Formel für V sind in Bild 3 zu sehen. Die Frequenzabhängigkeit ist durchaus wichtig, viele Dimensionierungstabellen oder Berechnungsschemen betrachten den Operationsverstärker als ideal und führen daher zu ungenauen Ergebnissen. Der Eingangswiderstand des Operationsverstärkers ist unendlich, der Ausgangswiderstand 0, was natürlich durch Hinzufügen von Elementen geändert werden kann. In der Regel kann man den Operationsverstärker jedoch ohne Ergänzungen übernehmen und erhält genügend genaue Ergebnisse. Wie schon erwähnt, darf die Ausgangsspannung den Versorgungsspannungsbereich nicht verlassen.
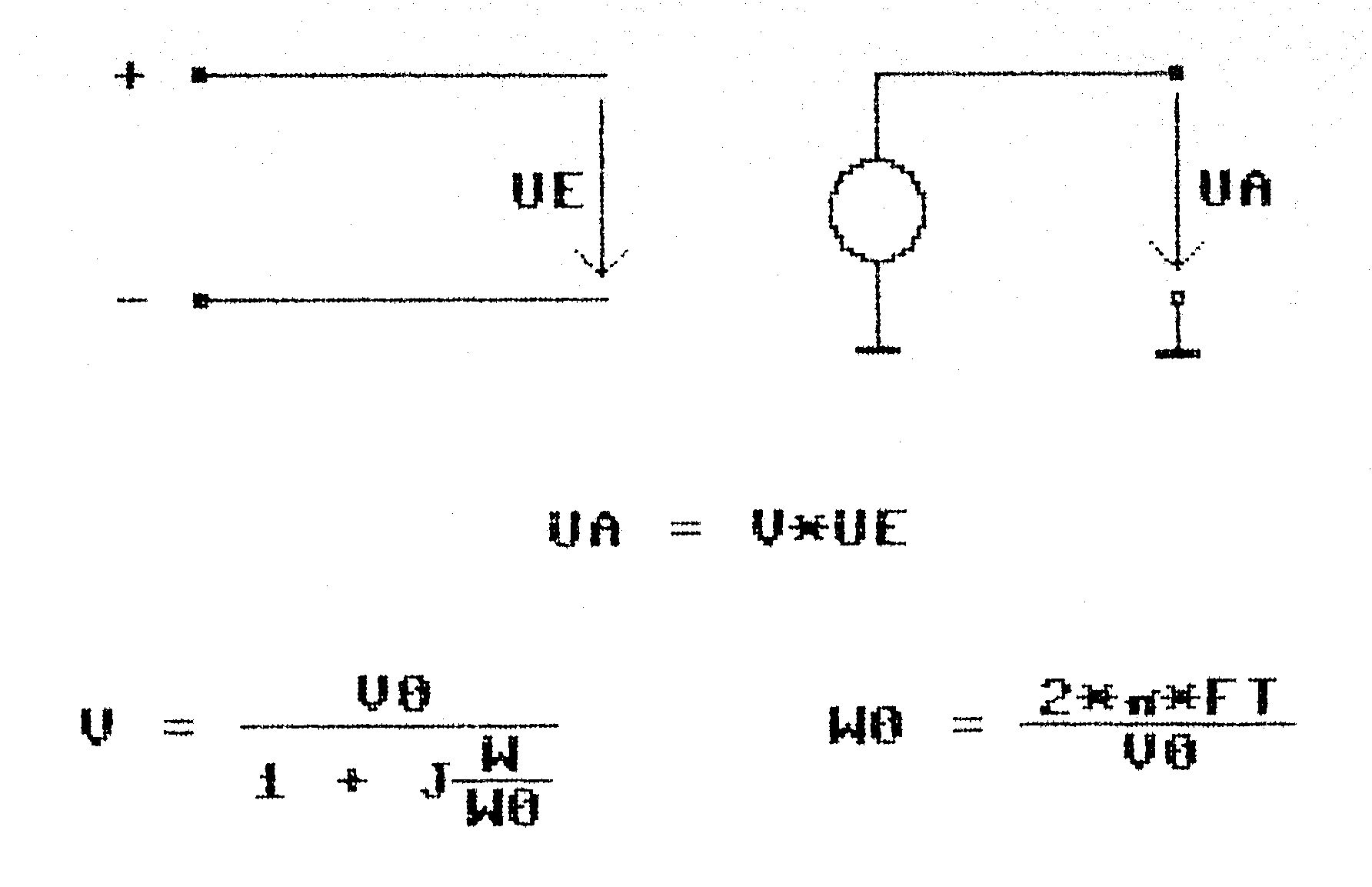
Als Daten für den Operationsverstärker muß nur seine Leerlaufspannungsverstärkung für tiefe Frequenzen V0 (zirka 105) sowie seine Transitfrequenz FT (einige MHz) eingegeben werden.
Der Vierpol
Ein Vierpol (oder richtiger: Zweitor) ist eine »Black Box« mit den Eingangsklemmen 1 und T und den Ausgangsklemmen 2 und 2' (siehe Bild 4). Seine Übertragungseigenschaften werden durch eine Matrix, die sogenannte Leitwertmatrix Y beschrieben. Diese Matrix besteht aus den Größen Y11, Y12, Y21 und Y22. Die Größen berechnen sich folgendermaßen:
- Y11 = I1/U1 bei U2 = 0 (sekundärer Kurzschluß)
- Y12 = I1/U2 bei U1 = 0 (primärer Kurzschluß
- Y21 = I2/U1 bei U2 = 0
- Y22 = I2/U2 bei U1 = 0
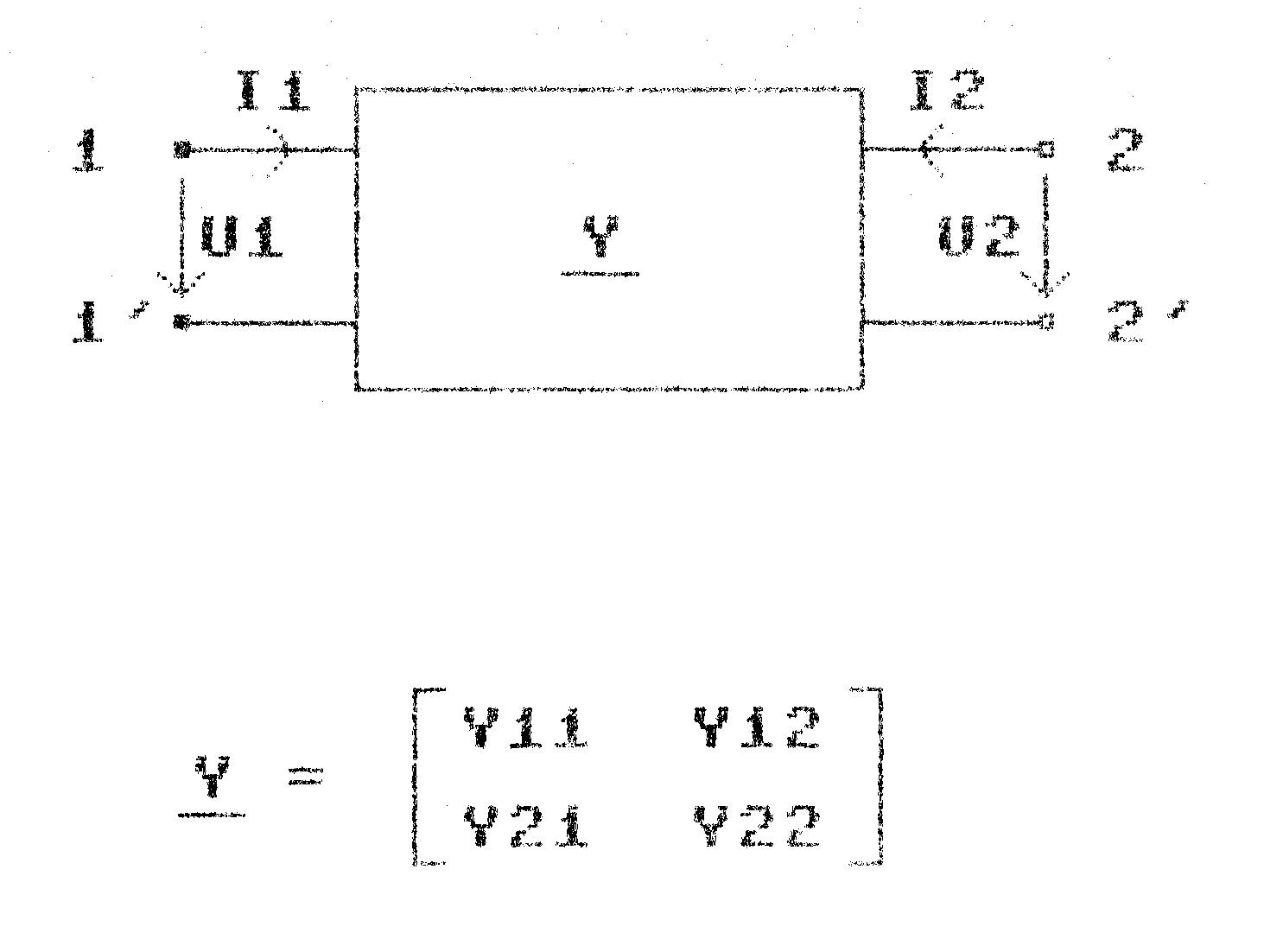
Außerdem lassen sich alle Ys in drei Teile zerlegen: Den ohmschen, den kapazitiven und den induktiven. Formelmäßig ausgedrückt:
Yij = 1/R + jωC + 1/jωI
wobei ω (Omega = 2 x pi x f = Kreisfrequenz und j eine komplexe Einheit ist.
Sie müssen für alle 4 Ys jeweils die Komponenten 1/R, C und 1/L eingeben, also insgesamt 12 Werte. Für einige Vierpole folgen noch Beispiele, dort werden Sie sehen, daß die Sache nur halb so schlimm ist, wie sie hier aussieht.
Das Wechselstrom-Ersatzschaltbild
Wir haben nun gesehen, wie sich verschiedene Elemente, teils dargestellt durch Ersatzschaltbilder, in das Programm eingeben lassen. Meist ist es jedoch nötig, die gesamte zu untersuchende Schaltung umzuformen. Da wir nämlich grundsätzlich nur das Wechselstromverhalten (Frequenzgang) einer Schaltung untersuchen, interessiert sich das Programm überhaupt nicht für Bauteile, die nur das Gleichstromverhalten der Schaltung etwas angehen. Das offensichtlichste Beispiel dafür sind die Versorgungsspannungen: Wechselspannungsmäßig gesehen ist eine Gleichspannungsquelle ein Kurzschluß und kann deshalb auch als solcher dargestellt werden. Das heißt die Versorgungsspannungsknoten erhalten wie die Masse die Nummer 0 und dürfen bei der Bestimmung der Knotenzahl nicht mitgezählt werden.
Auch Siebelkos sowie Koppelkondensatoren, die so groß sind, daß sie im betrachteten Frequenzbereich keinen Einfluß mehr haben, können durch Kurzschlüsse ersetzt werden.
Man kann dadurch Knoten und somit Rechenzeit sparen. Apropos Knoten sparen: Vielleicht ist Ihnen aufgefallen, daß wir in unserem ersten Beispiel, dem Bandpaß, die Widerstände R0 und R1 zusammenfassen können. Auch dadurch spart man einen Knoten und damit Rechenzeit, allerdings wollte ich nicht gleich am Anfang mit solchen Tricks kommen, um Sie nicht zu verwirren.
Im folgenden Kapitel wird es endlich wieder praktisch, es kommen die versprochenen Beispiele.
Beispiele, Tips und Tricks
Aktiver Klangregler
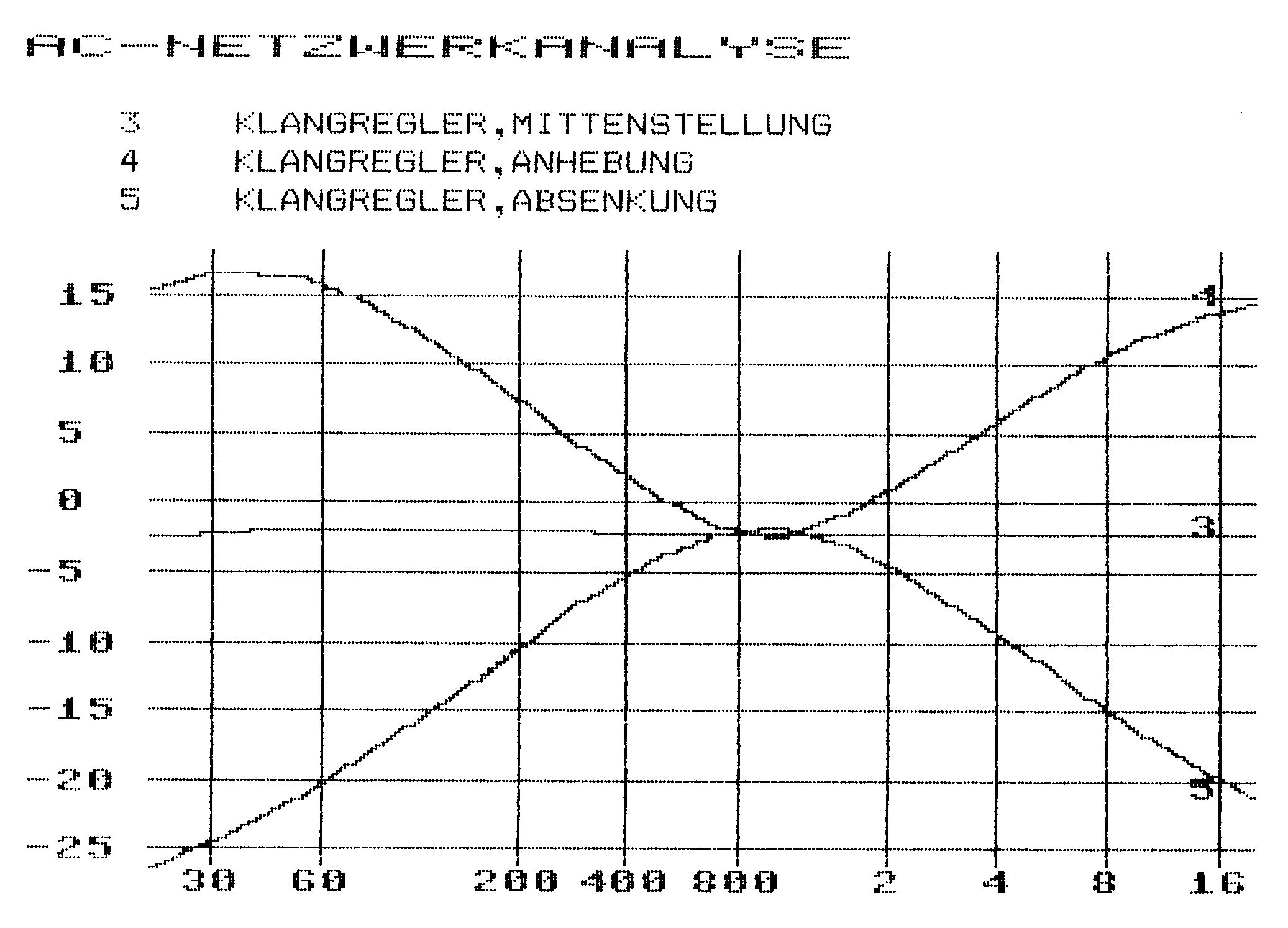
Bild 5 zeigt einen aktiven Klangregler, der wegen seiner Regelcharakteristik auch oft als »Kuhschwanzregler« bezeichnet wird: Die Enden des Frequenzganges lassen sich nämlich wie ein Kuhschwanz auf- und abschwenken.
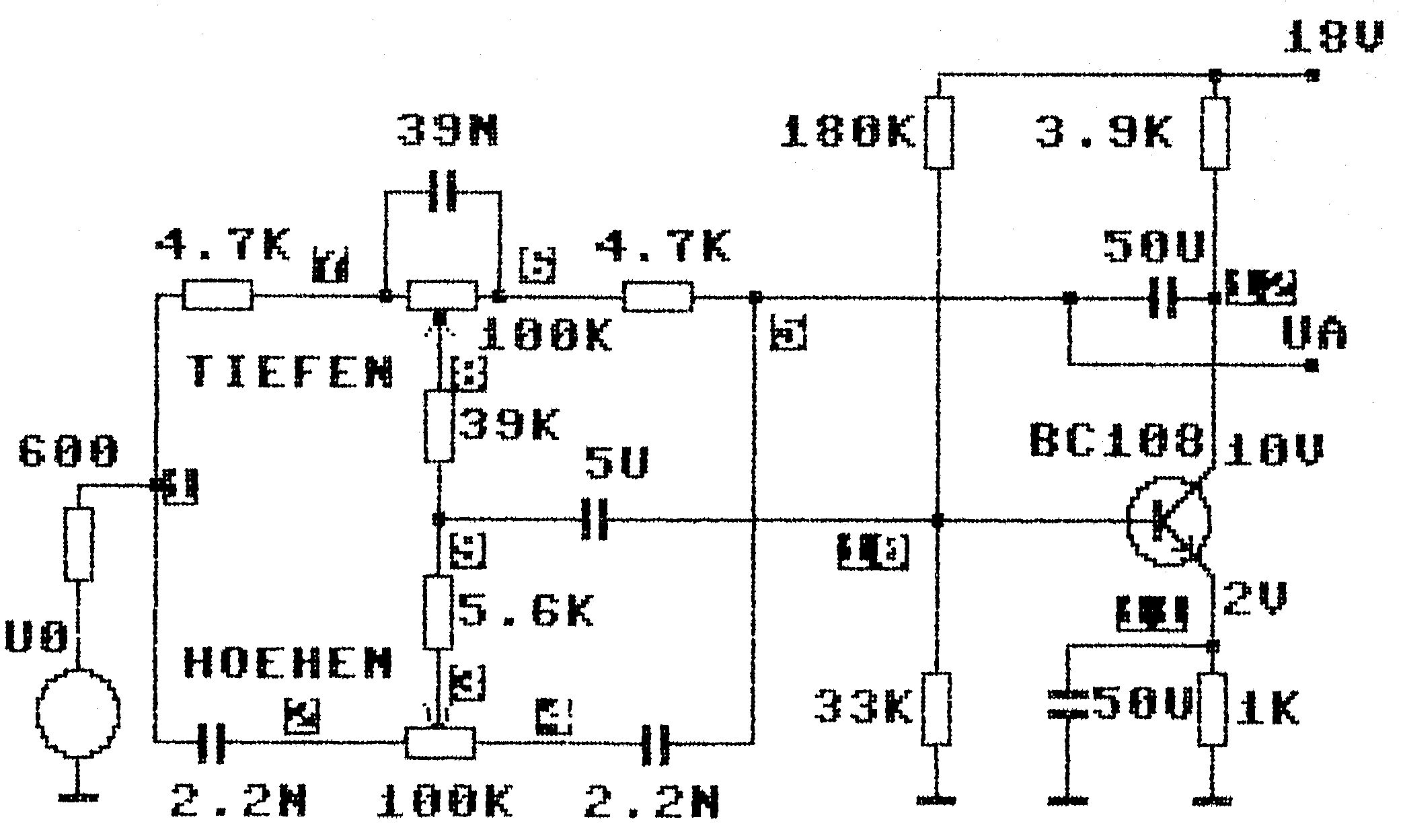
Sehen wir uns nun die Schaltung näher an: Bei der Knotennumerierung werde ich mich auf die im Bild angegebene beziehen, eine beliebige andere Reihenfolge wäre natürlich ebenso möglich. Beachten Sie, daß die 28-V-Versorgungsspannung keine eigene Knotennummer hat, sie bekommt wie die Masse die Nummer 0. Die beiden Potentiometer stellt man durch je zwei Widerstände dar, deren Summe den Gesamtwert von 100 kQ ergeben muß. Durch Variieren der beiden Werte läßt sich das Potentiometer »verstellen«, die Randpositionen lassen sich auch dadurch erreichen, daß man den Abgriff auf Knoten 2 oder 4 beziehungsweise 6 oder 7 umlegt (Widerstände mit dem Wert 0 können nicht eingegeben werden!).
Um Knoten zu sparen, hätte man, wie früher schon erwähnt, auch die großen Kondensatoren durch Kurzschlüsse ersetzen können. Allerdings haben diese — vor allem der 5 µF-Kondensator — im Bereich um 20 Hz schon einen spürbaren Einfluß. Experimentieren Sie doch hier ein wenig!
Der Kollektorstrom des Transistors im Arbeitspunkt läßt sich in diesem Beispiel sehr leicht ermitteln, da die Gleichspannungen am Kollektor und Emitter gegeben sind. Am Kollektorwiderstand (3.9 kΩ) fallen 8 V ab, das ergibt einen Kollektorstrom von IC = 8 V/3900 Ohm = 2 mA. Da der Emitterstrom ungefähr gleich dem Kollektorstrom ist, wäre es auch damit gegangen: IC = IE = 2 V/1 000 Ohm = 2 mA. In zwei der Beispielfiles wurde der Kollektorstrom um den Faktor 10 (!) nach oben und unten verändert, die Ergebnisse weichen dennoch nicht gewaltig vom richtigen Ergebnis ab (siehe Frequenzgangdiagramm dazu). Sie sehen daraus, daß die Eingabe dieses Wertes nicht sehr kritisch ist. Das gleiche gilt auch für die anderen beiden Transistorparameter B0 und FT. Ich empfehle Ihnen, hier im Einzelfall ein wenig herumzuprobieren, wie empfindlich eine Schaltung auf diese Eingabeparameter reagiert. In der Regel genügt für die Bestimmung dieser Werte die berühmte »Pi-mal-daumen«-Methode.
Man kann jedoch bereits aus dem Beispiel einige Zusammenhänge erkennen:
- B0 hat nur dann einen Einfluß, wenn der Transistor wenig rückgekoppelt ist, also verstärken soll.
- IC ist hauptverantwortlich für die Verstärkung. Bei zunehmender Verstärkung wird jedoch auch der Eingangswiderstand des Transistors verkleinert. Diese beiden Effekte können sich kompensieren (die Kurven für 0.2 mA und 20 mA sind fast gleich!). Mit zunehmendem IC wird auch die Grenzfrequenz des Transistors herabgesetzt.
- FT schließlich ist nur dann interessant, wenn der Transistor an seiner Frequenzgrenze betrieben wird.
Wie Sie gesehen haben, kann man aus der Beschaltung des Transistors seinen Kollektorstrom abschätzen. Natürlich muß auch hier, ebenso wie beim Operationsverstärker sichergestellt sein, daß der Transistor nur im aktiven Bereich betrieben wird. Das Programm erkennt eine Übersteuerung des Transistors nicht.
Übertragungsmaß
Das Übertragungsmaß ist das Verhältnis von Ausgangs- zu Eingangsspannung, also UA/U0. Dabei ist U0 die Leerlaufspannung der Quelle. Vielleicht haben Sie sich gewundert, daß der Klangregler eine Grunddämpfung von zirka 3 dB hatte, wo doch solche Schaltungen normalerweise für 0 dB Dämpfung dimensioniert sind. Hätte man die Spannung am Knoten 1 als Eingangsspannung genommen, dann wäre das auch rausgekommen. Sie können das leicht nachvollziehen, indem Sie den Quellwiderstand R0 ganz klein machen (zum Beispiel 1 Ohm). Dann ist die Spannung am Knoten 1 nämlich gleich U0. Das entspricht jedoch nicht der Praxis, denn auch dort hat die Quelle einen gewissen Innenwiderstand (Ausgangswiderstand der vorgeschalteten Stufe). Um diesen Sachverhalt zu berücksichtigen, verwendet die Definition des Übertragungsmaßes die Leerlaufspannung der Quelle.
Nun zur Ausgangsspannung: Das ist die Spannung an dem Knoten, den wir vorher als Ausgangsknoten angegeben haben, gemessen gegen Masse. In einer Brückenschaltung zum Beispiel interessiert uns aber die Brückenspannung UD, und die liegt nicht gegen Masse. Die Lösung dieses Problems ist jedoch ganz einfach: Wir nehmen einen Operationsverstärker mit der Leerlaufverstärkung V0 = 1 und einer Transitfrequenz FT, die deutlich über der höchsten Meßfrequenz liegt. An den Eingang dieses Operationsverstärkers legen wir die Brückenspannung und haben sie dann am Ausgang gegen Masse.
Nun wissen wir, wie U0 und UA definiert sind und können daraus das Verhältnis UA/U0 bilden. Dieses Verhältnis gibt man üblicherweise in dB (Dezibel) an, und zwar nach der Formel: Übertragungsmaß in dB = 20xlog(UA/U0) (dekadischer Logarithmus)
Beispiele zu Vierpolen
Transformator, lose gekoppelt:
| Y11 | = L2/1 |
| Y12 | = Y21 = -M/1 |
| Y22 | = L1/1 |
| dabei ist: | |
| 1 | = L1xL2/(M2) |
| L1 | = Induktivität an 1 1' |
| L2 | = Induktivität an 2 2' |
| M | = Gegeninduktivität = \(\mathrm{k \times \sqrt{L1 \times L2}}\), wobei k der Kopplungsfaktor ist (0<k<1). |
k darf den Wert 1 nicht erreichen (entspricht fester Kopplung), da sonst der Nenner 1 zu 0 würde. Ohm'sche Widerstände müssen in die Zuleitungen geschaltet werden, sie können nicht direkt in die Matrix aufgenommen werden, da der Vierpol keine inneren Knoten haben darf.
Idealer Gyrator
| Y11 | = Y22 = 0 |
| Y12 | = 1/r |
| Y21 | = —1/r |
| r | = Gyratorwiderstand |
Durch Kettenschaltung zweiter Gyratoren kann ein idealer Übertrager (k = 1, L1, L2 gegen unendlich) nachgebildet werden, wobei ü = r1/r2.
Da jedoch keine galvanisch getrennten Schaltungsteile entstehen dürfen, müssen Sie beide Seiten eines Übertragers oder Gyrators irgendwo »anhängen«. Ferner können noch Transistoren, FETs, Röhren und eben alles, was sich in einer Y-Matrix, wie unter »Vierpol« beschrieben, darstellen läßt, mit Vierpolen nachgebildet werden.
Beschränkungen des Programms
Eine Schaltung darf maximal 20 Knoten und 90 Bauelemente beinhalten, wobei Transistoren, Operationsverstärker und Vierpole doppelt zählen. Außerdem ist die Zahl der Vierpole auf vier begrenzt.
(Hans Haberl/ah)10 rem*********************************
20 rem* *
30 rem* newea2 *
40 rem* *
50 rem* von hans haberl *
60 rem* *
70 rem*********************************
100 rem steuerzeichen:
101 rem "{clr}" = shift + clr/home
102 rem "{down}" = crsr down
103 rem "{up}" = crsr up
104 rem "{left}" = crsr back
105 rem "{rvon}" = ctrl + 9
106 rem "{rvof}" = ctrl + 0
107 rem "{cyn}" = ctrl + 4
108 rem "{yel}" = ctrl + 8
109 rem "{lred}" = commodore + 3
110 rem "{gry3}" = commodore + 8
130 colour6,6:print"{clr}{gry3}":fill1,0,40,23,81,7:fill0,1,38,25,81,7:fchr3,3,34,19,32
150 printat(11,9)"ac-netzwerkanalyse":printat(12,15)"von hans haberl"
160 key1,"goto300"+chr$(13)
170 dimi,j,r,s,f,u,v,x,y,p,q,k,n,m,o,c,l,j1,j2,kf
180 dimx1,x2,y1,y2,xf,xs,yf,ys,tl,tp,t0,z,d,e,w,c$,x$,n$,l%,q%,i%
190 dimr(20,21),s(20,21),m%(20,21),k(20),y(2,20,20),f(9,20),u(9,20),w(9,20)
200 dimi(90),j(90),b(90),a(90),x(2,3,5),n(10),p(11)
210 dimc$(9),d$(9),e$(9),k$(9),b$(9)
220 tl=10/log(10):tp=180/~:t0=2*~:fori=0to9:readc$(i),d$(i),e$(i):nexti
230 dataf,knoten ,anzahl der ,a,widerstaende,r,d,kapazitaeten,c
240 datao,induktivitaeten,l,n,transistoren,c b e,e,y-vierpole,1 1' 2 2'
250 datal,op's,+ - a,s,frequenz,frequenzfile,0,0,r,0,0,w
280 i=0:repeat:getc$:i=i+1:untilc$<>""ori=300:print"{clr}":gosub500
300 close2:close4:close15
400 loop:print"{down}{down}>";:gosub5010
410 forc=0to7:ifc$<>c$(c)thennextc:gosub500:end loop
420 print:onc+1gosub1000,1000,1500,2000,3000,3300,4050,4000:end loop
500 print"{down}menue:":print"n=netzwerk eingeben":print"e=elemente eingeben"
510 print"f="d$(7)"gang":print"a=ausgabe":print"d=diagramm"
520 print"l=daten laden":print"s=daten speichern":return
1000 c$="":gosub5650:gosub5700:ifq=0thenp=0:return
1010 i=q:ifc<1andu<9thenprintd$(7)"en von ";:gosub5700
1020 rcomp:ifq>0andf(q,0)>0thenforj=0tof(q,0)+1:f(i,j)=f(q,j):nextj
1030 rcomp:ifc=0thenprint"ohne aenderung ?";:gosub5010
1040 q=i:l=0:input"notiz";k$(q):ifc<1thenw(q,0)=c:ifc$<>"j"thenl=1
1080 gosub1400:ifp<3orc<0thenreturn
1100 c=1:loop:print"file{rvon}#{rvof} , {rvon}n{rvof}ormierung oder {rvon}d{rvof}rucker?";
1110 gosub5010:j=asc(c$)-48:l=0
1120 ifc$="n"thengosub1300:end loop
1130 ifc$="d"thengosub7200:end loop
1140 exit ifj<1orj>9:exit iff(j,0)=0
1150 gosub1200:end loop:return
1200 gosub5900:p=1:l=1:repeat:f=f(q,p):iff(j,l)<fthenf=f(j,l)
1220 c$=str$(f):printright$(c$,len(c$)-1):print"{up}";
1230 iff=f(q,p)thenprinttab(7)"{cyn}";:x=u(q,p)
1240 rcomp:gosub5950:printtab(23):x=w(q,p):gosub5950:print:print"{up}{gry3}";:p=p+1
1250 iff=f(j,l)thenprinttab(15):x=u(j,l)
1260 rcomp:gosub5950:printtab(31):x=w(j,l):gosub5950:l=l+1
1270 print:untilp>f(q,0)orl>f(j,0)
1280 printtab(10)"{cyn}file"q"{gry3}file"j:return
1300 input"bezugsfrequenz";f:input"db-wert";s:fori=1tof(q,0)
1310 iff=f(q,i)thenr=s-u(q,i):fori=1tof(q,0):u(q,i)=u(q,i)+r:nexti
1320 rcomp:gosub1400:return
1330 nexti:return
1400 gosub5900:forp=1to20
1410 iff(q,p)=0andc=0thenl=1
1420 ifl=1thenprintf(q,p);:inputf(q,p):print"{up}{up}"
1430 iff(q,p)>0thenonc+2gosub6000,4400,4700:nextp
1440 f(q,0)=p-1:return
1500 gosub5750:q=p:ifq=0thenreturn
1600 gosub1700:fori=1toq:forj=1tof(p(i),0):x1=x2:y1=y2
1610 x2=log(f(p(i),j))*xf+xs:y2=u(p(i),j)*yf+ys
1620 ifj>1thenlinex1,y1,x2,y2,1:linex1+1,y1,x2+1,y2,1
1630 nextj:ifq>1thencharx2-18,y2-6,p(i)+48,1,1
1640 nexti:gosub5050:nrm:print"{down}ausgabe auf drucker ?";:gosub5010
1650 ifc$="j"thengosub7300
1660 return
1700 x1=f(p(1),1):x2=x1+1:y2=u(p(1),1):y1=y2-1
1710 fori=1toq:p=p(i):r=f(p,f(p,0)):s=f(p,1):ifr>x2thenx2=r
1720 ifs<x1thenx1=s
1730 forj=1tof(p,0):r=u(p,j):ifr>y2theny2=r:else:ifr<y1theny1=r
1740 nextj,i:yf=185/(y1-y2):ys=192-y1*yf:xf=288/log(x2/x1):xs=32-log(x1)*xf
1750 hires6,4:s=(y2-y1)/10:r=10^int(log(s)/log(10)+.2):s=r*int(s/r+1)
1760 i=0:repeat:i=i+1:y=s*int(y1/s+i)
1770 ify<y2thenv=y*yf+ys:text0,v-3,str$(y),1,1,8:line32,v,319,v,1
1780 untily>y2
1800 ifx2/x1>1.1thengosub1820:else:gosub1860
1810 return
1820 s=log(x2/x1)/10:v=x2-x1:x=x1
1830 repeat:r=10^int(log(x*v/(x+v))/log(10)):x=r*int(x/r+1):gosub1900
1840 x=x*exp(s):untilx>x2:return
1860 s=(x2-x1)/6:r=10^int(log(s)/log(10)+.2):s=r*int(s/r+1)
1870 i=0:repeat:i=i+1:x=s*int(x1/s+i):gosub1900:untilx>x2:return
1900 u=x:loop:exit ifu<1000:u=u/1000:end loop:c$=right$(str$(u),5)
1910 u=log(x)*xf+xs:textu-4-4*len(c$),193,c$,1,1,8:lineu,0,u,191,1:return
2000 c=-1:gosub1000:gosub5000:ifc$="j"orp<2thenreturn
2010 l%=p-1:c=6:gosub5660:ifu>0thenp(10)=p(1):else:p(10)=9-int(q/9)
2020 repeat:print"optimierung von max. 4 elementen"
2030 p=1:repeat:printp".element "b$(p);:inputb$(p):gosub6050:untilp>4
2040 gosub5000:untilc$<>"j":p(0)=9-p:ifp=9thenreturn
2050 p(9)=q:p=p(10):f(p,0)=l%:w(p,0)=1:k$(p)="ist":z=1:q%=10:print"x=abbruch"
2100 loop:l=2:q=p(q%):forp=1tol%:f(q,p)=f(p(9),p):gosub4400:exit ifr=0
2110 w(q,p)=u(q,p)-u(p(q%-1),p):nextp
2130 forj=10toq%:u=-r:r=0:forp=1tol%:r=r+w(p(q%),p)*w(p(j),p)/w(p(9),p)^2
2140 nextp,j:ifq%=11thens=(1+atn(u/r/6)/3)^2:gosub3500:q%=10:end loop:z=0:return
2150 print:print"zyklus"z"fehler:"r:forp=1top(0):printb$(p),b(p(p));
2160 iflen(b$(p))>4thenprintb(p(p+4)):else:print
2170 nextp:getc$
2180 ifc$="x"orr<1thenprint"abbruch?";:gosub5010:exit ifc$="j"orc$="x"
2200 q%=11:i%=mod(z,p(0))+1:z=z+1:s=1.1:d=b(p(i%)):e=b(p(i%+4)):gosub3500
2210 end loop:z=0:return
3000 j=j1:fori=1to5:p(i)=n(i):nexti:repeat:print"{down}"e$(0);d$(0)"(ohne 0)",n;
3010 inputn:fori=1to6:printe$(0);d$(i)tab(30)n(i);:inputn(i):n(i)=abs(n(i))
3020 nexti:gosub5000:gosub5600
3030 untilj1<91andn>0andn<21andn(6)<6andc$<>"j"
3040 m=1:j=j+j1:fori=1to5:p=m+p(i)*(1+int(i/4)):m=m+n(i)*(1+int(i/4))
3050 ifp>mthenfork=mtoj:gosub5620:nextk
3060 ifp<mthenfork=jtomstep-1:gosub5620:nextk
3070 nexti:repeat:k=1:fori=1to6:ifn(i)>0thenprint"{down}"d$(i)" an "d$(0)
3080 rcomp:forj=1ton(i):onigosub5100,5100,5100,5150,5200,5150:gosub5250:nextj
3090 nexti:repeat:print"{down}ausgangs"d$(0),n(9);:inputn(9)
3100 untiln(9)>0andn(9)<=n
3110 gosub5000:untilc$<>"j":print
3300 repeat:k=0:j(0)=1:fori=1to6:ifn(i)>0ori=1thenprint:printd$(i)" "e$(i)
3310 rcomp:forj=sgn(i-1)ton(i):onigosub5300,5300,5300,5350,5450,5400
3320 rcomp:k=k+1+int(i/4):nextj
3330 nexti:gosub5000:untilc$<>"j"
3500 ifz>0thenb(p(i%))=d*s:b(p(i%+4))=e*s^sgn(49-p(i%+4))
3600 gosub6200:u=-1:m=n+1:fori=1ton:forj=1tom:m%(i,j)=0:nextj,i
3610 k=1:j2=1:forl=0to2:fori=1ton:forj=1ton:y(l,i,j)=0:nextj,i
3620 j2=j2+n(l+1):loop:exit ifk=j2:i=i(k):j=j(k):gosub5800:k=k+1
3630 end loop:nextl:y(0,1,1)=y(0,1,1)+1/b(0):m%(1,m)=u
3650 j2=j2+2*n(4):loop:exit ifk=j2:l=0:s=abs(b(k))/.026:r=s*5e-4:p=i(k+1):o=i(k)
3660 i=p:j=o:gosub5820:j=j(k):r=s:gosub5820:o=j:r=s/a(k):gosub5820
3670 l=1:r=s/t0/b(k+1):gosub5820:i=i(k):p=i:r=r*5e-4:gosub5820:k=k+2:end loop
3700 s=1:j2=j2+2*n(5):loop:exit ifk=j2:i=i(k):j=j(k):p=i:o=j:kf=0:gosub5850
3710 i=i(k+1):j=j(k+1):kf=1:gosub5850:p=i:o=j:kf=3:gosub5850
3720 i=i(k):j=j(k):kf=2:gosub5850:s=s+1:k=k+2:end loop
3750 j2=j2+2*n(6):loop:exit ifk=j2:l=i(k+1):fori=0to2:forj=1ton:y(i,l,j)=0
3760 nextj,i:y(0,l,l)=1:m%(l,l)=u:m%(l,i(k))=u:m%(l,j(k))=u
3770 a(k)=t0*b(k+1)/b(k):k=k+2:end loop:j2=j2-2*n(6)
3780 fori=1ton:m%(i,0)=i:nexti
3790 p=n(9):ifp<nthenq=n:gosub6300
3800 fori=1ton-1:forj=i+1ton:m%(i,j)=m%(i,j)orm%(j,i):m%(j,i)=m%(i,j):nextj,i
3810 ifn<3then3920
3820 forp=1ton-2:f=n*n:fork=pton-1:v=0:fori=pton-1
3830 ifm%(i,k)thenforj=i+1ton:w=m%(k,j)andnotm%(i,j):v=v-w:nextj
3840 nexti:v=2*v-m%(k,m):ifv=fthengosub6350:ifr>sthens=r:q=k
3850 ifv<fthenf=v:q=k:gosub6350:s=r
3860 nextk:ifq>pthengosub6300
3870 iff=0then3910
3880 fori=p+1ton-1
3890 ifm%(i,p)thenforj=i+1ton:m%(i,j)=m%(i,j)orm%(p,j):m%(j,i)=m%(i,j):nextj
3900 nexti
3910 nextp
3920 fori=1ton:m%(i,m)=m%(i,m)orm%(i-1,m):k(m%(i,0))=i:nexti:gosub6250
3930 ifz>0thenreturn
3950 print"ausgabe auf drucker?";:gosub5010:ifc$="j"thengosub7000
3960 return
4000 f=0:open15,8,15:print"schaltung speichern ?";:gosub5010
4010 ifc$="j"andn*j1>0thengosub4100
4020 print:iff=0thenprinte$(7)"s speichern ?";:gosub5010:ifc$="j"thengosub4300
4030 close2:close15:return
4050 open15,8,15:gosub5500
4060 iff=0theninput#2,c$:ifright$(c$,5)="newea"thenonval(c$)gosub4110,4300
4070 close15:close2:return
4100 gosub5500:iff>0thenreturn:else:print#2,"1newea":input"notiz";n$
4110 print:ifc=7thenprint#2,chr$(34)+n$+chr$(34):else:input#2,n$:printn$
4120 n(0)=n:fori=0to9:ifc=7thenprint#2,n(i):else:input#2,n(i)
4130 nexti:n=n(0):gosub5600:fori=0toj1
4140 ifc=7thenprint#2,i(i):print#2,j(i):print#2,b(i):print#2,a(i):else:input#2,i(i),j(i),b(i),a(i)
4150 nexti:ifn(5)=0then4190
4160 fork=1ton(5):fori=0to2:forj=0to3
4170 ifc=7thenprint#2,x(i,j,k):else:input#2,x(i,j,k)
4180 nextj:nexti:nextk
4190 gosub5550:close2:iff=0andc=6thengosub3300
4200 return
4300 onc-5gosub5660,5750:ifp=0orc+u=16thenreturn
4310 ifc=7thengosub5500:iff=0thenprint#2,"2newea":print#2,p:else:iff>0thenreturn
4330 ifc=6theninput#2,p:ifp>uthenprint"nur"u"von"p:p=u
4340 fori=1top:q=p(i)
4345 ifc=6theninput#2,k$(q):printq;k$(q):else:print#2,chr$(34)+k$(q)+chr$(34)
4350 j=0:repeat:ifc=6theninput#2,f(q,j),u(q,j),w(q,j)
4360 ifc=7thenprint#2,f(q,j):print#2,u(q,j):print#2,w(q,j)
4370 j=j+1:untilj>f(q,0):f(q,j)=0:nexti:gosub5550:return
4400 gosub6200:s=t0*f(q,p):ifs=0orn=0thengosub6400:return
4410 fori=1ton:u=k(i):forj=1ton:v=k(j):s(u,v)=y(1,i,j)*s-y(2,i,j)/s
4420 r(u,v)=y(0,i,j):nextj:s(i,m)=0:r(i,m)=0:nexti:r(k(1),m)=1/b(0)
4450 k=j2:loop:exit ifk=j2+2*n(6):i=k(i(k+1)):ifi=0then4490
4460 r=1+s*s/a(k)^2:u=b(k)/r:v=u*s/a(k)
4470 j=k(i(k)):r(i,j)=r(i,j)-u:s(i,j)=s(i,j)+v
4480 j=k(j(k)):r(i,j)=r(i,j)+u:s(i,j)=s(i,j)-v
4490 k=k+2:end loop
4500 fork=1ton-1:u=r(k,k):v=s(k,k):f=u*u+v*v
4510 iff=0thengosub6400:return
4550 fori=k+1ton:ifnotm%(i,k)then4600
4560 x=r(i,k):y=s(i,k):r=(x*u+y*v)/f:s=(y*u-x*v)/f:forj=k+1tom
4580 ifm%(i,j)then:x=r(k,j):y=s(k,j):r(i,j)=r(i,j)-r*x+s*y:s(i,j)=s(i,j)-s*x-r*y
4590 nextj
4600 nexti,k:u=r(n,n):v=s(n,n):f=u*u+v*v:iff=0thengosub6400:return
4610 x=r(n,m):y=s(n,m):r=(x*x+y*y)/f
4620 gosub6250:ifr=0thenprint"ua=0":p=p-1:l=1:return
4630 u(q,p)=tl*log(r):ifl=2thenreturn
4640 r=x*u+y*v:s=y*u-x*v
4650 ifs=0thenw(q,p)=(1-sgn(r))*90:else:w(q,p)=90*sgn(s)-tp*atn(r/s)
4700 x=f(q,p):printx;:printspc(12-len(str$(x)));:x=u(q,p):gosub5950
4710 x=w(q,p):printspc(7):gosub5950
4720 print:ifl=0orp<2thenreturn
4750 f=f(q,p):u=u(q,p):v=w(q,p):forj=pto2step-1
4760 iff(q,j-1)>fthenf(q,j)=f(q,j-1):u(q,j)=u(q,j-1):w(q,j)=w(q,j-1):nextj
4770 f(q,j)=f:u(q,j)=u:w(q,j)=v:return
5000 print"{down}korrektur? ";
5010 flash7,20:print"{yel} {gry3}";:gosub5050:print"{left} {left}"c$:off:return
5050 poke198,0:wait198,1:getc$:return
5100 print" "e$(i);j,i(k);j(k);:inputi(k),j(k):return
5150 print" "left$(d$(i),i-3);j,e$(i);i(k);j(k);i(k+1);
5160 inputi(k),j(k),i(k+1):j(k+1)=0:return
5200 repeat:print" vp"j,e$(i):printi(k);j(k);i(k+1);j(k+1);
5210 inputi(k),j(k),i(k+1),j(k+1):untilj(k+1)<=n:return
5250 forq=ktok+i/4
5260 ifi(q)<0orj(q)<0orn<i(q)orn<j(q)thenj=j-1:return
5270 nextq:k=q:return
5300 repeat:gosub6500:inputb(k):untilb(k)<>0:return
5350 repeat:gosub6550:inputa(k),b(k),b(k+1):untilb(k+1)>0anda(k)>0:return
5400 repeat:gosub6600:inputb(k),b(k+1):untilb(k+1)>0:return
5450 gosub6650:forl=0to3:gosub6660
5460 inputx(0,l,j),x(1,l,j),x(2,l,j):nextl:return
5500 repeat:print:input"filename ($=directory)";n$:ifn$="$"thenprint:dir"$:*=s"
5510 print:gosub5550:iff>0thenreturn
5520 untiln$<>"$":open2,8,2,n$+",s,"+e$(c+2)
5550 pause1:input#15,f,c$,r,s:iff>0thenprintf;c$;r;s
5560 return
5600 j1=n(1)+n(2)+n(3)+2*(n(4)+n(5)+n(6)):return
5620 q=k+p-m:i(k)=i(q):j(k)=j(q):b(k)=b(q):a(k)=a(q):return
5650 print"{down}{down}":printe$(7)"belegung:"
5660 u=0:fori=1to9:k=f(i,0):ifk=0thenu=u+1:p(u)=i
5670 ifk>0andc<>6thenprinti":"k$(i):print" "k"freq :"f(i,1)"-"f(i,k)
5680 nexti:print:p=u:return
5700 repeat:repeat:printe$(7)" (1-9)"q;:inputq
5710 untilq>=0andq<=9:untilf(q,0)>0orc<1orq=0:return
5750 gosub5650:repeat:fori=1to9-u:printi".";:q=p(i):gosub5700:p(i)=q
5760 ifq>0thennexti
5770 p=i-1:gosub5000:untilc$<>"j":return
5800 p=i:o=j:ifl=1thenr=b(k):else:r=1/b(k)
5820 ifi=jorp=othenreturn
5830 y(l,p,i)=y(l,p,i)+r:y(l,o,j)=y(l,o,j)+r:m%(p,i)=u:m%(o,j)=u
5840 y(l,p,j)=y(l,p,j)-r:y(l,o,i)=y(l,o,i)-r:m%(p,j)=u:m%(o,i)=u:return
5850 forl=0to2:r=x(l,kf,s):ifr<>0thengosub5820
5860 nextl:return
5900 print:printd$(7);spc(5)"betrag (db) ";
5910 ifw(q,0)=0thenprint"phase (grad)":else:print"toleranz(db)"
5920 return
5950 x$=str$(sgn(x)*int(abs(x)*1e3+.5))
5960 loop:exit iflen(x$)>4:x$=insert("0",x$,1):end loop
5970 x$=insert(".",x$,len(x$)-3):use"####.###",x$:return
6000 printdup(" ",10)"{up}":printf(q,p)tab(8):x=u(q,p):gosub5950:inputu(q,p)
6010 repeat:print"{up}"tab(23):x=w(q,p):gosub5950
6020 inputw(q,p):untilw(q,p)>0:gosub4750:return
6050 r=1:c$=b$(p):l=len(c$):ifc$="0"thenp=10-p:return
6060 fori=1to3:forj=rtor+2:ifmid$(c$,j,1)<>e$(i)thennextj,i:return
6070 k=val(right$(c$,l-j)):ifk<int(i/2)ork>n(i)thenreturn
6080 forj=1toi:k=k+n(j):nextj:k=k-n(i):p(p+4)=k:ifr=1then6120
6100 fori=3to4:n$=mid$(c$,i,1)
6110 ifn$="*"thenp(p+4)=k+50:else:ifn$<>"/"thennexti:return
6120 ifr=1thenp(p)=k:r=4:ifl>4then6060:else:p=p+1:return
6200 print"{lred}{rvon}*** busy ***{gry3}":return
6250 print"{up}"dup(" ",14)"{up}":return
6300 fori=1ton:r=m%(i,p):m%(i,p)=m%(i,q):m%(i,q)=r:nexti
6310 forj=0tom:r=m%(p,j):m%(p,j)=m%(q,j):m%(q,j)=r:nextj:return
6350 r=u:forj=1ton:r=r-m%(k,j):nextj:return
6400 gosub6250:r=0:print"nicht loesbar":p=p-1:l=1:return
6500 print" "e$(i);j"("i(k);j(k)")",b(k);:return
6550 print" t"j"("i(k);j(k);i(k+1)") b0,ic,ft":printa(k);b(k);b(k+1);:return
6600 print" op"j"("i(k);j(k);i(k+1)") v0,ft":printb(k);b(k+1);:return
6650 print" vp"j"("i(k);j(k);i(k+1);j(k+1)") 1/r c 1/l":return
6660 print" y"11+8*int(l/2)+l;x(0,l,j);x(1,l,j);x(2,l,j);:return
6700 gosub6650:forl=0to3:gosub6660:print:nextl:return
7000 input"notiz";n$:gosub7400:print" "n$
7020 k=0:fori=1to6:ifn(i)>0ori=1thenprint:printd$(i)" "e$(i)
7030 rcomp:forj=sgn(i-1)ton(i):onigosub6500,6500,6500,6550,6700,6600
7040 rcomp:print:k=k+1+int(i/4):nextj
7050 nexti:print:print"ausgangsknoten:",n(9):print#4:close4:return
7100 gosub7400:print"optimierungsverlauf":print#4:close4:return
7200 gosub7400:print" "k$(q):gosub1400:print#4:close4:return
7300 gosub7400:fori=1toq:ifq>1thenprint" "p(i);
7310 print" "k$(p(i)):nexti:print:print#4:close4:copy:return
7400 open4,4:cmd4:print:printchr$(14)"ac-netzwerkanalyse"chr$(15)
7410 print:return
