Klangsynthese und Synthesizertechnik

Unser Commodore 64 ist ein hervorragender Musikus. Manches Musikprogramm läßt ihn sogar teurere, professionelle Musiksynthesizer übertreffen. Will man ihm selbst gezielt Töne entlocken, muß man über einige grundlegende Dinge der Klangsynthese und Synthesizertechnik Bescheid wissen.

Drei verschiedene Kurvenformen und sogenanntes »weißes Rauschen« stellt der Sound-Chip des Commodore 64 für unsere Experimente zur Verfügung. Die drei Kurvenformen nennt man Dreieck, Rechteck und Sägezahn (siehe Bild 1).

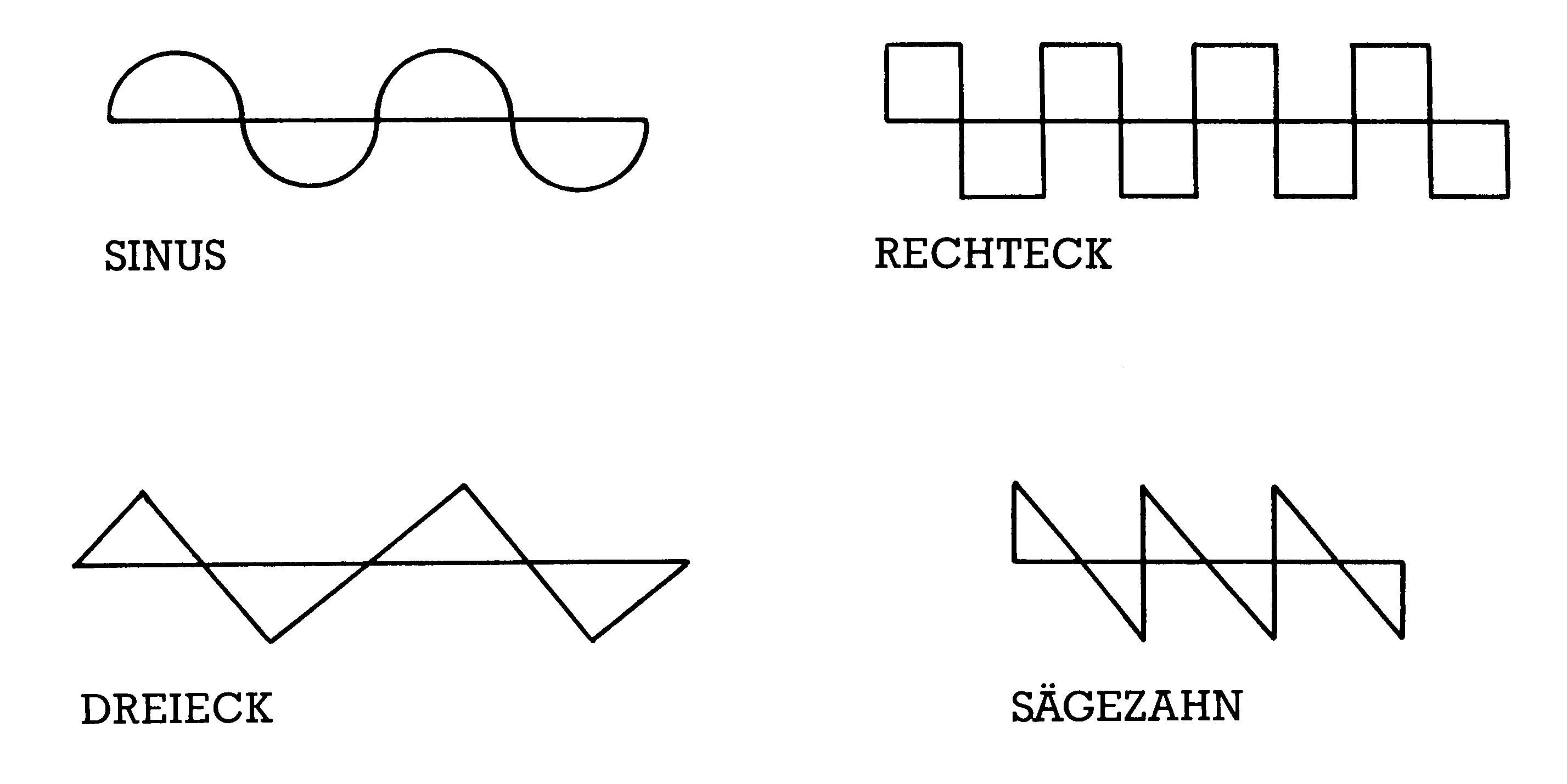
Jede der drei Kurven klingt ganz charakteristisch und zwar unabhängig von der Tonhöhe. Keine der drei klingt identisch mit irgendeinem natürlichen Instrument. Leider, sonst wäre nämlich alles viel einfacher. Bei den genannten Schwingungsformen handelt es sich um sehr einfache Basiskurven. Betrachtet man Kurvenformen natürlicher Klangerzeuger, also etwa eines Musikinstruments oder irgend eines anderen Geräusches am Oszillograph, stellt man sehr viel kompliziertere Kurvenverläufe fest (siehe Bild 2).

Außerdem verändern sich die Kurven kontinuierlich während des gesamten Klangablaufes. Wie lassen sich so komplexe Abläufe elektronisch realisieren?

Zu Beginn des 19. Jahrhunderts lebte der französische Mathematiker Jean Baptiste Joseph Fourier. Er entwickelte die mathematisch-physikalischen Grundlagen, die uns auch heute noch Klänge verstehen und elektronisch nachahmen lassen. Es handelt sich um das Verfahren der sogenannten harmonischen Analyse von Klängen. Heute nennen wir das zugrundeliegende mathematische Prinzip ihm zu Ehren Fourier-Synthese. Fourier stellte fest, daß sämtliche periodischen Schwingungen in eine sinusförmige Grundschwingung und ebenfalls sinusförmige Oberschwingungen zerlegt werden können. Man nennt diese auch harmonische Oberschwingungen oder einfach Harmonische. Diese unterscheiden sich nur in der Frequenz und der jeweiligen Amplitude. Er bewies auch, daß die Umkehrung dieses Satzes ebenso gilt.

Unterschiedliche Obertongemische produzieren verschiedene Klänge

Jede periodische Schwingung läßt sich durch Addition ihrer Grundkomponenten, also Sinusschwingungen mit bestimmter Frequenz und Amplitude, aufbauen. Sein Beweis war natürlich rein mathematischer Natur. Prinzipiell handelt es sich hier um Mathematik in Reinkultur. Natürlich bestehen nicht alle Klänge aus periodischen Schwingungsverläufen. Deshalb kann man mit diesem Verfahren auch nicht alle Klänge analysieren beziehungsweise synthetisieren. Rauschen ist zum Beispiel eine absolut nicht periodische Schwingungsform und kann nicht nach diesem Verfahren behandelt werden. Für die Frequenzen der Harmonischen gilt die Bedingung, daß sie in einem geradzahligen Verhältnis zur Frequenz der Grundschwingung stehen. Die Reihen der möglichen Sinuskurven haben also alle denselben Frequenzabstand, nämlich die Frequenz der Grundschwingung. Die Grundschwingung ist die Sinuskurve mit der tiefsten Frequenz. Sie bestimmt meist gleichzeitig die Tonhöhe des Klangs. Die Harmonischen bestimmen den Charakter des Klanges.

Wie ein Ton nun letztlich klingt, bestimmt die Zusammensetzung seines Obertongemisches. Entscheidend ist, welche Harmonischen beteiligt sind und mit welcher Amplitude. Betrachten wir wieder unsere Grundschwingungsformen. Hier handelt es sich um reine periodische Grundschwingungen. Sie lassen sich auch sehr leicht mit Mitteln der Elektronik erzeugen. Deshalb sind sie für uns so wichtig.

Der Sinuston besitzt keine Oberschwingungen, er ist rein. Sein Klang hört sich unnatürlich weich an. Reine Sinustöne existieren in der Natur nicht. Ganz anders der Sägezahn. In einer Sägezahnschwingung sind alle Obertöne vertreten. Der n-te Oberton ist hierbei 1/n mal so laut wie der Grundton. Die Amplitude der Obertöne nimmt also hier mit zunehmender Ordnungszahl ab. Der Sägezahn klingt hell, trompetenhaft. Die Dreieckschwingung weist sehr viel weniger Obertöne auf. Sie klingt dumpf. Man kann den Klang auch als flötenähnlich bezeichnen. Die Rechteckschwingung besteht aus ungeradzahligen Obertönen. Sie klingt hohl.

Bob Moog konstruierte den ersten Synthesizer

Bob A. Moog hatte als erster die Idee, diese Grundschwingungsformen zur Klangsynthese einzusetzen. Inspiriert von den Klangwünschen seines Freundes Herb Deutsch, eines Experimental-Musikers, hatte er den Sommer 1964 damit verbracht, Elektronik-Module zu konstruieren, die die absonderlichsten Klänge hervorbrachten. Mit diesen Modulen war es erstmals möglich, die drei Größen, mit denen sich jedes Klangereignis beschreiben läßt, nämlich Tonhöhe (Frequenz), Klangfarbe (Kurvenform-Oberwellengehalt) und Lautstärke (Amplitude) relativ genau zu kontrollieren. Die entscheidende Idee war die Einführung der Spannungssteuerung. Er entwickelte Module, die direkt diesen drei Größen zuzuordnen und mittels Spannungssteuerung elektronisch kontrollierbar waren.

So entstand der Moog-Synthesizer, ein Klangmonster von 1 x 2 m Größe. Dieses Gerät revolutionierte die gesamte elektronische Tonerzeugung grundlegend. Auch unser kleiner SID-Chip ist prinzipiell nichts anderes als ein Nachfolger des Riesenkastens von einst. Nur mit dem Unterschied, daß er aus wenigen Kubikzentimetern Raum Leistung zaubert, für die ehedem der Moog-Synthesizer Kubikmeter benötigte und statt analoger Technik und Spannungssteuerung Digitaltechnik und Digitalkontrolle einsetzt.

Eines hat jedoch der Moog von einst dem SID-Chip von heute immer noch voraus. Er klingt wesentlich besser. SID-Klänge sind nicht sehr bombastisch. Es fehlen volle Bässe und höchste Höhen. Deshalb konnte sich auch bisher der Commodore 64 mit dem SID bei Profimusikern als Instrument nicht etablieren.

Im folgenden möchte ich kurz die einzelnen Funktionsgruppen eines Synthesizers, wie es auch unser SID ist, beschreiben.

Töne und Melodien entstehen in Tongeneratoren. Unser SID stellt uns drei unabhängig voneinander funktionierende Tongeneratoren zur Verfügung. Jeder produziert drei verschiedene Kurvenformen, nämlich Dreieck, Sägezahn und Rechteck. Überdies erzeugt jeder noch weißes Rauschen, ein Gemisch sämtlicher Frequenzen, die von einem Zufallsgenerator erzeugt werden.

Töne entstehen in Oszillatoren

Wir haben gehört, daß sich unsere Basis-Kurvenformen durch ihren unterschiedlichen Gehalt an Obertönen und somit durch ihren Klang prinzipiell unterscheiden. Nach einigem Üben mit dem SID wissen wir bald, welche Kurvenform sich für einen bestimmten Klang anbietet.

Verschiedene Kurvenformen, schön und gut, aber wozu drei Tongeneratoren? Ganz einfach. Musik besteht nicht nur aus Solo-Melodien. Mit einem Tongenerator alleine könnten wir kaum Musik produzieren. Drei Tongeneratoren lassen uns jedoch schon ein ganzes Kammermusik-Trio realisieren. Das heißt, wollen wir drei verschiedene Töne gleichzeitig erzeugen, also dreistimmig polyphon spielen, muß für jeden Ton ein eigener Tongenerator vorhanden sein.

Der Rauschgenerator — kein Sturm ist ihm heilig

Mit dem Rausch-Generator (Noise-Generator) ist es möglich, Effekte wie Wind und Brandung zu erzeugen, den Klang einer Pauke oder eines Beckens, den Anblaswind von Orgelpfeifen, Holzblasinstrumenten und schließlich Gewehrschüsse in allen Variationen nachzuahmen.

Ein Ton macht nun aber noch lange keine Musik. Viele Töne unterschiedlicher Tonhöhe sind hierzu nötig. Deshalb muß die Tonhöhe der Oszillatoren steuerbar sein. Wie wir schon wissen, erfand Moog das Prinzip der Spannungssteuerung. Sämtliche Module seines Synthesizers konnten von analogen Steuerspannungen geregelt werden. Man nannte deshalb die Module auch »voltage controlled modules« (spannungsgesteuerte Module).

Computer hantieren nur ungern mit analogen Spannungen. Auch die Tongeneratoren unseres SIDs werden deshalb nicht von Analogspannungen, sondern mittels digitalen Informationen gesteuert. Wir nennen diese Oszillatoren deshalb auch nicht VCOs (voltage controlled oscillators), wie dies Moog machte, sondern besser DCOs (digital controlled oscillators).

Musiker wollen mit ihrem Instrument spielen. Es soll Töne produzieren. Wie teilen wir unseren Tongeneratoren mit, welche Töne sie spielen sollen? Routinierte Klavierspieler möchten ihre Ideen am liebsten über eine Klaviatur einspielen. Leider verfügt der Commodore 64 über keine richtige. So bleibt nichts anderes, als die Alpha-Tastatur in ein Keyboard zu verwandeln. Hierzu ordnet man jeder QWERTY-Taste eine Tonfrequenz zu. Drückt man die Taste, erklingt der Ton. Das Spielen auf einer Schreibmaschinentastatur bereitet jedoch wenig Freude, zumindest muß man sich erst daran gewöhnen.

Kürzlich erschienen jedoch zwei Klaviaturen auf dem Markt, die mit richtigen Klaviertasten ausgerüstet, an den Commodore 64 angeschlossen werden können. Ihre Anschaffung lohnt sich sicher für den, der mit dem Commodore ausschließlich Musik machen will und eine Klaviertastatur gewöhnt ist.

Viele beherrschen das Klavierspiel jedoch nicht. Sie können trotzdem Musik mit dem Commodore 64 komponieren. Die Kompositionen werden nun nicht »Live« eingespielt, sondern Ton für Ton über die Alpha-Tastatur eingetippt. Es spielt dabei keine Rolle, in welcher Geschwindigkeit die Eingabe erfolgt. Man kann sich also viel Zeit lassen und Eingabefehler nachträglich ausbessern. Die einzelnen Töne werden hierbei mittels mehreren Eingaben für Tonhöhe, Tondauer und Lautstärke bestimmt. Das Verfahren ist relativ langwierig. Hat man alles eingegeben, spielt der Commodore den Song in der gewünschten Geschwindigkeit ab.

Bei den meisten ordentlichen Musikprogrammen kann der Computer die eingespielten oder eingetippten Songs speichern und auf Befehl wieder ausgeben. Die Länge der Kompositionen kann hierbei meist einige tausend Töne betragen. Ein Moog-Synthesizer von einst konnte sich nur 16 Töne merken und diese zyklisch immer wieder abspielen. Man nannte Geräte, die dies ermöglichten, Sequenzer. Heute benutzt man diesen Begriff meist allgemein für Tonspeichersysteme.

Wir sagten schon, daß sich jeder Klangeindruck durch die drei Größen Tonhöhe, Klangfarbe und Lautstärke beschreiben läßt. Wir wissen nun, daß die Töne in den Oszillatoren entstehen und die Tonhöhe durch digitale Steuerung dieser Oszillatoren entsteht. Außerdem können wir durch Auswahl der Kurvenformen bereits unterschiedliche Klangfarben erhalten. Wie können wir nun die Lautstärke bestimmen?

Der ADSR steuert den Lautstärkeverlauf der Klänge

Der Klang eines Klaviers weist ein ähnliches Frequenzspektrum wie der einer Geige auf. Trotzdem unterscheiden sich die beiden Klänge voneinander gravierend. Eine wesentliche Ursache hierfür ist der unterschiedliche zeitliche Verlauf der Lautstärken. Schlägt man eine Klaviersaite an, setzt der Ton schlagartig ein und schwillt dann relativ rasch wieder ab. Im Gegensatz dazu schwillt der Geigenklang langsam an und behält, solange der Bogen gestrichen wird, eine konstante Lautstärke bei. Erst wenn der Bogen nicht mehr über die Saite streicht, klingt der Ton langsam ab. Klavier und Geige unterscheiden sich also im zeitlichen Verlauf der Lautstärke in der sogenannten »Hüllkurve«.

Jedes Instrument, jedes Geräusch zeichnet sich vor allem durch einen ganz spezifischen Lautstärkenverlauf aus. Hier spielen sich sehr komplexe Vorgänge ab, und nicht zuletzt bestimmt die Möglichkeit, solche komplexe Hüllkurven nachzubilden, die Qualität eines Synthesizers. Moog reduzierte bei der Entwicklung seines Synthesizers den Verlauf der Hüllkurve auf die Nachbildung der für das menschliche Klangempfinden wichtigsten vier Phasen: Attack, Decay, Sustain und Release (ADSR). Zu Deutsch: Anstieg, Abfall, Aushalten und Freigabe des Lautstärkeverlaufes. Der sogenannte ADSR- oder Hüllkurvengenerator liefert nun eine dem gewünschten Hüllkurvenverlauf entsprechende Steuerinformation. In unserem SID handelt es sich hierbei wieder um Digitalinformationen, die direkt die Lautstärke der drei Tongeneratoren beeinfllussen. In Analogsynthesizern benutzt man auch in diesem Fall Steuerspannungen. Unser SID stellt drei ADSRs zur Verfügung. Jede Stimme kann folglich einen eigenen Hüllkurvenverlauf erhalten. In Bild 3 sehen wir links eine typische ADSR-Kurve. Auf der x-Achse ist die Zeit, auf der y-Achse die Amplitude (Lautstärke) des Klanges abgetragen. Sofort nach dem Anschlag einer Taste würde die Lautstärke des Tons zunächst langsam bis zum Maximum ansteigen (Attack) und dann auf einem bestimmten Sustainpegel einige Zeit verweilen (Sustain). Läßt man die Taste los, verklingt er in der Abklingphase (Release), bis man nichts mehr hört. Natürliche Attack-Werte liegen, je nach Klang, im Bereich von einigen Millisekunden bis zu einigen Sekunden. Kurze Attack-Werte besitzen alle percussiven Instrumente wie Pauke, Schuß, auch Saiten-Instrumente wie Gitarre und Klavier gehören hierzu. Längere Attack-Zeiten finden wir zum Beispiel bei Blasinstrumenten. Es dauert, bis die Atemluft des Trompeters das Instrument zum Klingen bringt. Streichinstrumente weisen noch längere Attack-Werte auf. Sehr lange Attack-Zeiten, im Bereich vieler Sekunden, benötigt man zum Beispiel, um Wind oder Brandungsgeräusche nachzuahmen. Hat der Ton dann den maximalen Attack-Pegel mehr oder weniger schnell erreicht, können wir ihn in der ebenfalls regelbaren Decay-Phase bis auf einen gewissen Pegel abfallen lassen, den Sustain-Pegel.

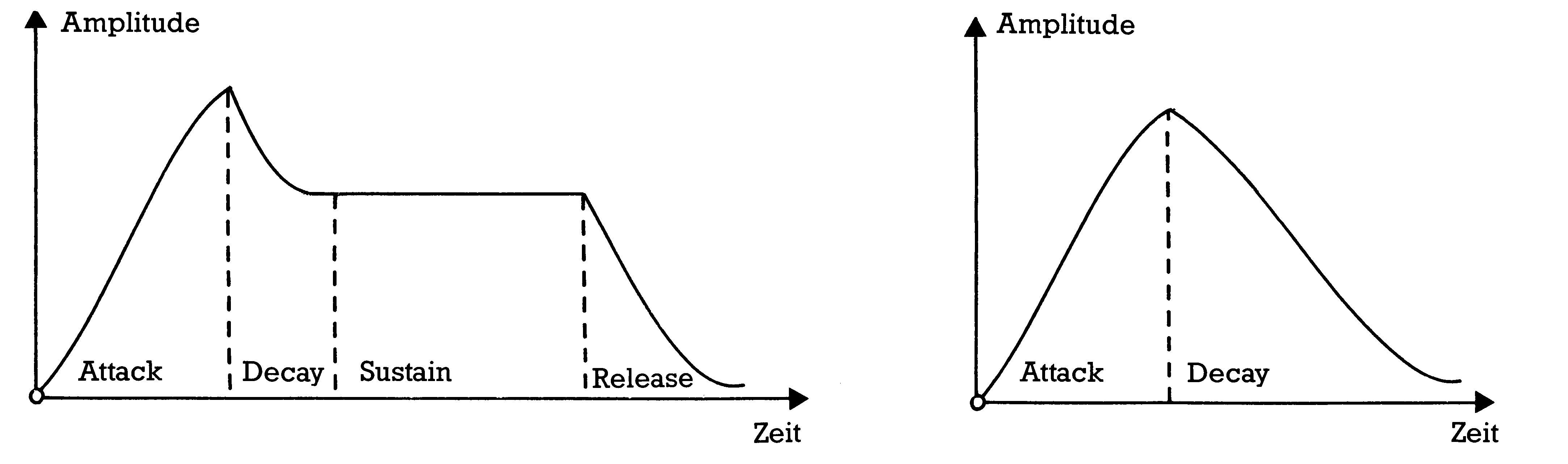
Wie lange der Ton den Sustain-Pegel beibehält, bestimmt das Gate-Signal. Solange unser Gate gleich 1 ist, bleibt der Ton auf dem durch den eingestellten Sustain-Pegel bestimmten Lautstärkeniveau. Wird das Gate-Signal gleich 0, geht der Ton in die letzte der vier Phasen, die Release-Phase über.

Die Release-Phase bestimmt, in welcher Zeit unser Ton vom Sustain-Pegel auf die Lautstärke Null abfällt. Sobald unser Gate gleich 0 wird, beginnt die Release-Phase. Natürliche Instrumente besitzen nur kurze Release-Phasen. Man denke zum Beispiel an ein Klavier. Läßt man die Tasten nach dem Anschlag wieder los, verklingt der Ton relativ schnell. Die Zeit des Tastendrucks entspricht der Zeit, die wir unser Gate-Signal auf dem Wert 1 halten, also eingeschaltet haben müssen. Manche Klänge durchlaufen nicht alle vier Phasen der Hüllkurve. Denken wir zum Beispiel an die Orgel. Der Orgelton erklingt fast augenblicklich nach dem Anschlagen einer Taste und verlischt ebenso schnell wieder. Der elektronisch erzeugte Klang benötigt im Vergleich zu einem natürlichen Instrument keine Zeit, um sich aufzubauen, und es schwingt auch kein Resonanzkörper nach. Um das zu realisieren, müßten wir Attack, Decay und Release gleich Null setzen, den Sustain-Pegel auf Maximum einstellen. Percussionsinstrumente wiederum verfügen nur über Attack und Decay. Trifft der Schlegel die Pauke, baut sich der Ton fast sofort auf. Genau so schnell klingt er jedoch wieder ab. Man kann ihn nicht durch längeres Drücken auf das Fell in eine Sustain-Phase zwingen. Ein Beispiel für so eine percussive Hüllkurve sehen wir rechts in Bild 3.

Unser SID-Chip wird digital gesteuert

Durch Auswahl verschiedener Grundschwingungsformen können wir unsere Klänge schon in bestimmte Richtungen lenken. Wir können diese Grundklänge jedoch noch weiter verändern.

Jede Stereo-Anlage verfügt über einen Klangregler. Wie jeder weiß, kann man mit diesem die Musik hell oder dumpf klingen lassen. Elektronisch wird dies mit einem Filter realisiert. Solche Filter kann man mit Kaffee-Filtern vergleichen. Diese halten Kaffekörnchen bestimmter Größe zurück. Ab einer bestimmten Größe können sie nicht mehr durch die Filterporen schlüpfen. Unsere Elektronik-Filter tun auch nichts anderes. Nur daß sie nicht Kaffeepartikel bestimmter Größe aufhalten, sondern harmonische Oberschwingungen bestimmter Frequenz. Wie wir bereits wissen, verändert dies unseren Gesamtklang unter Umständen beträchtlich. Nimmt man zum Beispiel alle Oberschwingungen höherer Frequenz weg, wird der Klang immer dumpfer. Nimmt man alle tieffrequenten Oberschwingungen weg, klingt der Ton heller. Auf diese Weise können wir also unsere Grundwellenformen nochmals entscheidend im Klang verändern.

Filter bestimmen, ob unser Ton hell oder dumpf klingt

Unser SID stellt zunächst drei verschiedene Grundfiltertypen zur Verfügung. Der Hochpaßfilter läßt alle hochfrequenten Oberschwingung passieren. Die Tiefen schneidet er ab. Leitet man einen Klang hindurch, klingt er am Schluß heller als zuvor. Der Tiefpaßfilter stellt das Gegenteil unseres Hochpasses dar. Er beschneidet die hohen Klanganteile, läßt tiefe ungehindert passieren. Die Klänge klingen dann dumpfer als vorher. Der dritte Filtertyp ist der Bandpaßfilter. Er läßt ein bestimmtes Frequenzband passieren, schneidet alle darüber- und darunterliegenden Frequenzanteile ab. Die Klänge werden dadurch flach.

Bei allen drei Filtertypen kann man die jeweilige Filterfrequenz bei der sie wirken sollen, genau einstellen.

Neben diesen drei Hauptfiltertypen, kann unser SID durch Mischung dieser drei, noch weitere Mischfiltertypen erzeugen.

Neben der Filterfrequenz existiert noch eine weitere wichtige klangbestimmende Größe, die Filterresonanz. Eine Gitarre klingt völlig anders als eine Geige, auch wenn man bei beiden die selben Töne spielt. Dies rührt von der unterschiedlichen mechanischen Bauweise der Resonanzkörper der beiden Instrumente her. Eine Elektrogitarre ohne solchen klingt ohne angeschlossenen Verstärker fast gar nicht. Der Resonanzkörper ist für den Klang verantwortlich. Er dient bei unseren Instrumenten gewissermaßen als Klangverstärker. Die Bauweise entscheidet hierbei, welche Frequenzen besonders verstärkt werden, welche weniger. Dieses Phänomen nennt man Resonanz.

Bei unserem elektronischen Filter kann natürlich kein Gehäuse mitschwingen. Die Resonanz wird elektronisch erzeugt. Welche Frequenzen dabei besonders angehoben werden sollen und welche nicht, können wir mit der sogenannten Filterresonanz einstellen. Auf diese Weise läßt sich das Resonanzverhalten natürlicher Instrumente simulieren.

Unser Sound-Chip besitzt nur einen Filter. Durch diesen müssen alle drei Tonoszillatoren geleitet werden. Sie lassen sich folglich nicht unabhängig voneinander mit diversen Filtereinstellungen versehen. Wir können aber für jeden Oszillator bestimmen, ob er den Filter durchlaufen soll oder nicht. Wir können die Oszillatoren, also auch um den Filter herum, direkt in den Verstärker leiten.

Ein weites Feld an Klangeffekten eröffnen Ringmodulation und Synchronisation von Oszillatoren. Ich möchte hier weniger auf die theoretischen Grundlagen dieser beiden Effekte eingehen. Nur so viel sei gesagt, in beiden Fällen wird ein Oszillatorsignal mit einem zweiten, von einem anderen Oszillator, moduliert.

Bei der Ringmodulation multipliziert man die Frequenzen der beteiligten Oszillatoren miteinander. Es entsteht dann eine neue Frequenz, die viele nicht harmonische Obertöne enthält. Im SID werden natürlich keine Frequenzen sondern digitale Zahlenwerte multipliziert. Auf diese Weise kann man vor allem metallische oder glockenähnliche Klänge synthetisieren.

Synchronisiert ein Oszillator einen anderen, so zwingt er diesen dazu, seine Kurvennulldurchgänge den eigenen anzupassen. Vor allem, wenn beide Oszillatoren unterschiedliche Frequenz aufweisen, ergeben sich hier interessante Klangeffekte.

So, dies war nun die graue Theorie, zumindest die erste Lektion auf dem steinigen Weg, dem SID-Chip Töne, Klänge und Musik zu entlocken. In einer weiteren Lektion werden wir lernen, mit welchen Befehlen wir die Parameter der Oszillatoren, Hüllkurvengeneratoren, des Filters und des Ringmodulators unseres SID-Chips ansprechen können.