»Kudiplo« erfüllt Schülerträume
Eine komplette Kurvendiskussion ist für Computerbesitzer eine ganz einfache Angelegenheit.
Wer hätte sich da nicht gewünscht, solche lästige Arbeit nähme ihm ein fleißiger Computer ab. Diesen Wunsch erfüllt »Kudiplo« jedenfalls für den, der einen VC 20 mit wenigstens 3 KByte Erweiterung besitzt. Für den C 64 ist »Kudiplo« leicht einzurichten. Nur die Bildschirmbefehle sind anzupassen.
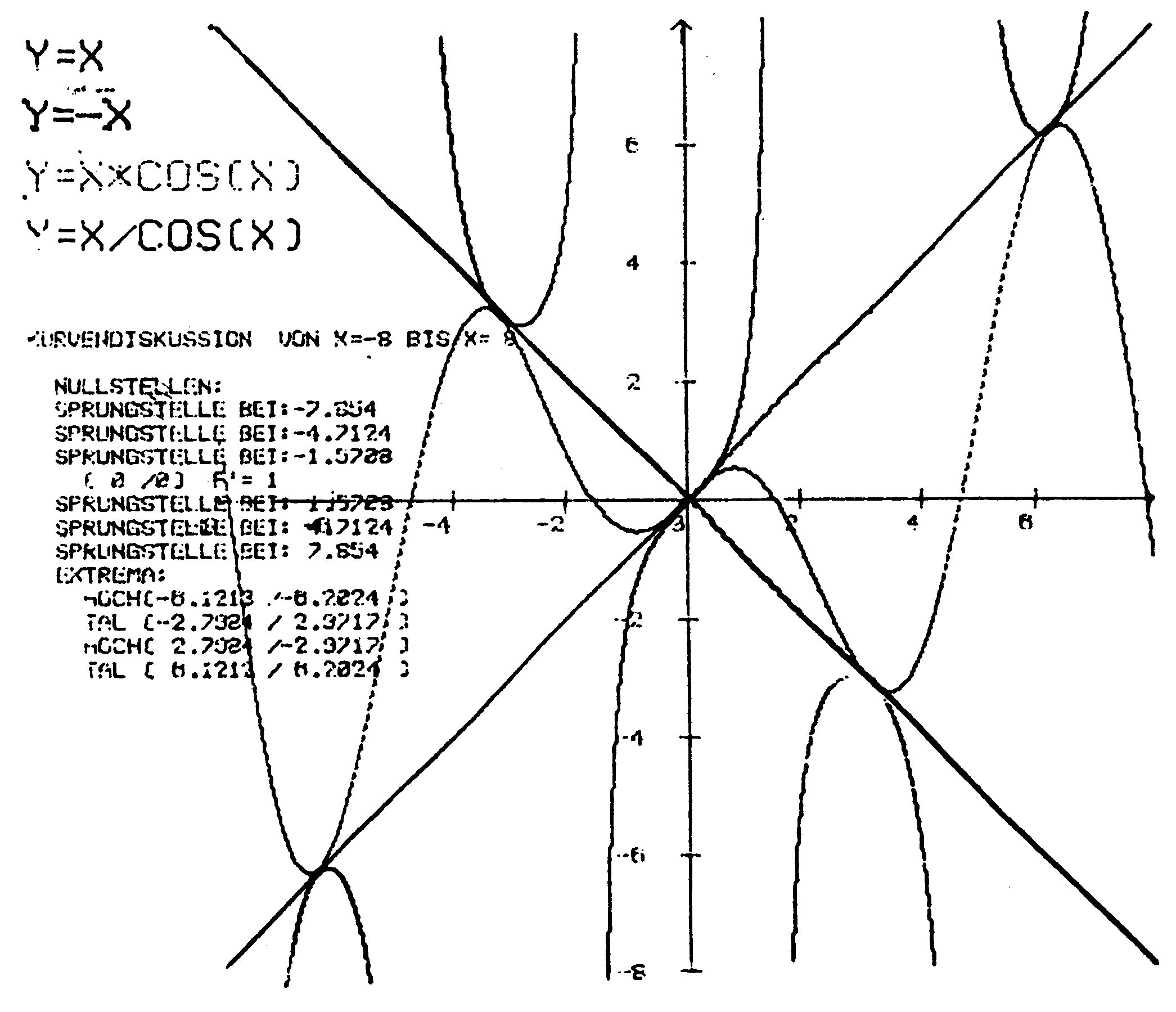
Benötigt wird außerdem der VC 1520, der Printer-Plotter von Commodore der die grafische Darstellung mit einer Präzision möglich macht, die keine Wünsche offen läßt. Mit »Kudiplo« kann dann jede beliebige mathematische Funktion im frei wählbaren Bereich und Maßstab dargestellt werden. Außerdem wird auf Wunsch eine Kurvendiskussion ausgedruckt mit Nullstellen, Sprungstellen und Extrema, deren Koordinaten bis zur vierten Dezimalstelle genau berechnet werden.
Hier die besonderen Fähigkeiten des Programmes:
- Auf beiden Koordinatenachsen kann der dargestellte Bereich frei gewählt werden durch Bestimmung des jeweils untersten und obersten Wertes.
- Die zweckmäßigste Positionierung der Koordinatenachsen wird automatisch ermittelt (Normalfall: Kreuzung im Nullpunkt).
- Entsprechend dem gewählten Bereich wird die Skalierung des Achsenkreuzes berechnet und in die Grafik geschrieben.
- Die Maßeinheit beider Achsen beträgt dabei immer 10 mm, so daß Zwischenwerte leicht aus der Grafik ausgemessen und berechnet werden können.
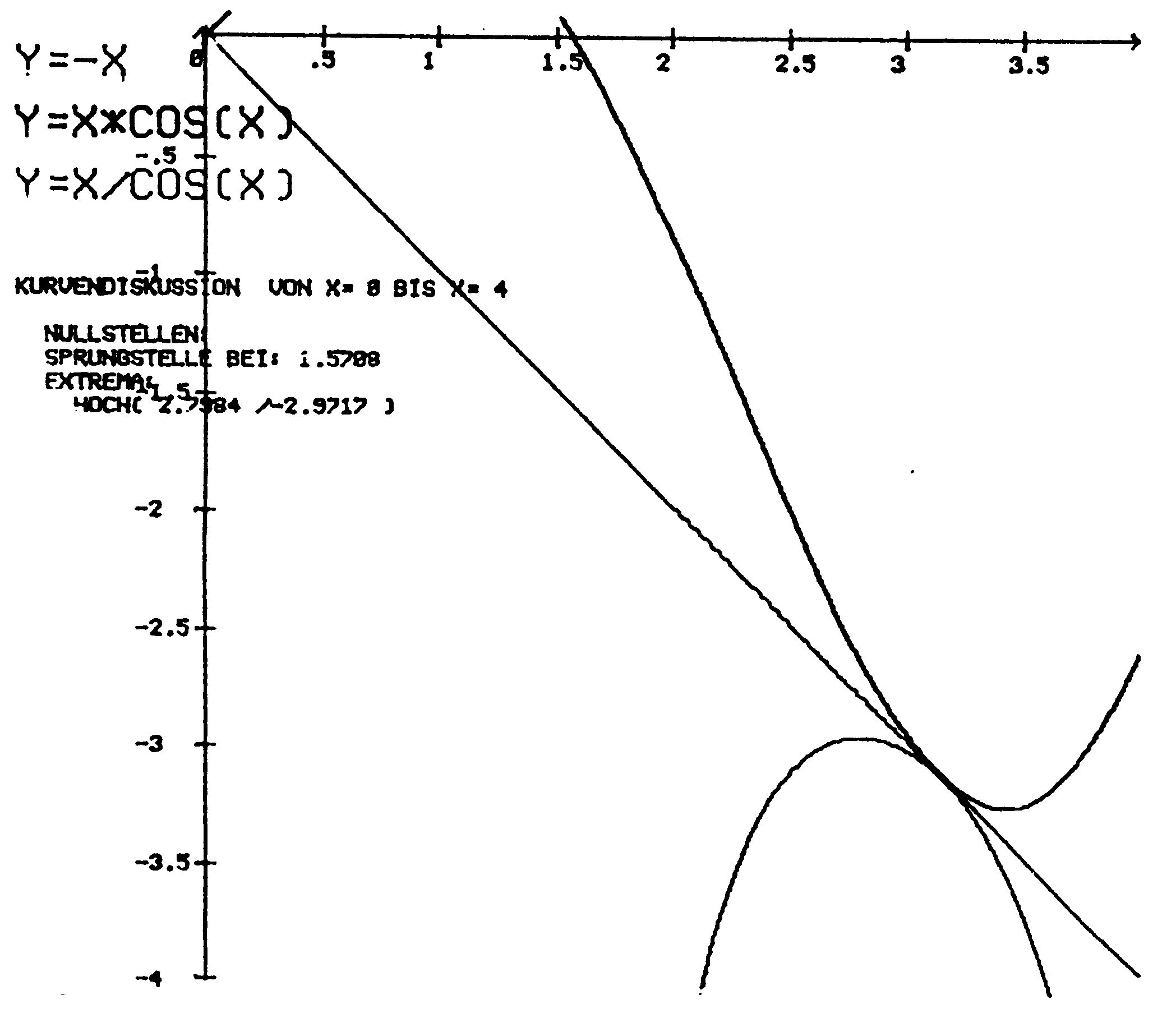
- Der frei wählbare Darstellungsbereich macht es möglich, durch Wahl eines Teilbereiches Ausschnittvergrößerungen der Funktion in jedem beliebigen Maßstab darzustellen (!).
- In ein Achsenkreuz kann nach der ersten auch noch eine zweite und beliebig oft noch eine weitere Funktion (etwa zum Vergleich mit der ersten) geplottet werden — solange nicht mit »Paper feed« der Papiertransport betätigt wurde.
- Jede Funktion wird in anderer Farbe gezeichnet und die zugehörige Gleichung mit gleicher Farbe in die Grafik eingetragen.
- Auf Wunsch wird von der zuletzt dargestellten Funktion die Kurvendiskussion erstellt.
- Dabei werden ermittelt: Extrema, Maxima, Minima und Sattelpunkte sowie die Nullstellen unter Angabe der Steigung und die Sprungstellen mit ihren Koordinaten.
- Verarbeitet werden alle dem VC 20- (beziehungsweise C 64) geläufigen mathematischen Funktionen. Bei ihrer Eingabe ist nur auf die Einhaltung der üblichen Syntax zu achten.
- Ein besonderer Vorzug von »Kudiplo« ist schließlich, daß das Programm unzulässige Werte erkennt und unberücksichtigt läßt SQR(X) führt darum bei Werten von X < 0 ebensowenig zum Abbruch des Programms wie 1/X bei X = 0.
Die Gebrauchsanleitung für den Benutzer wird über den Bildschirm angegeben. Unlogische Eingaben werden zurückgewiesen.
Das Programm erfragt zuerst den Bereich, in welchem die Funktion dargestellt wird (Zeilen 470 bis 540). Die entsprechenden Werte werden in den Variablen XU, XO, YU und YO gespeichert. Aus diesen Werten wird die Lage des Nullpunktes auf beiden Achsen (XN und YN) und die Maßeinheit für die Skalierung der Achsen (XE und YE) berechnet. Weiter wird anschließend die darzustellende Funktion in den Zeilen 585 bis 620 erfragt.
Die folgende Routine dient dazu, die Funktion in das Programm zu übernehmen, indem sie zusammen mit ihrer Ableitung in die Programmzeilen 65 bis 80 und 205 geschrieben wird. Die Routine bedient sich dabei des bekannten Verfahrens der Eingabe über Bildschirmspeicher und Tastaturpuffer:
Die zu verändernden Zeilen werden auf den Bildschirm geschrieben, dann wird der Tastaturpuffer mit der erforderlichen Zahl von »RETURNs« gefüllt Bei dem dann folgenden Programmabbruch (Zeile 660) arbeitet der Computer die Befehle im Tastaturpuffer ab Damit bei der hiermit bewirkten Änderung des Programmes die zuvor gewählten Parameter nicht verloren gehen, werden auch diese (mit Eingabe in die Zeilen 45 und 50) gerettet. Damit diese Routine funktioniert, dürfen die Zeilennummem 45, 50, 65, 70 und 205 nicht verändert werden!!
Nachdem sich das Programm durch »GOTO 45« selbst wieder gestartet hat, werden zunächst die Parameter aus den Zeilen 45 bis 55 und aus den Zeilen 65 bis 80 die definierten Funktionen eingelesen.
Nun endlich kann der Plotter in Funktion treten. Er zeichnet die X-Achse (Zeilen 100 bis 140) und die Y-Achse (Zellen 145 bis 165) in der Größe von 400 x 400 Druckersteps (= 8 x 8 cm).
Es folgt in den Zeilen 195 bis 225 die Berechnung der Funktionswerte, beginnend mit dem niedrigsten Wert von X und mit der Schrittweite J von normalerweise 1/400 des Gesamtbereichs. Wer die Ausgabe (auf Kosten der Auflösung) beschleunigen möchte, erreicht dies durch Zuweisung eines höheren Wertes für J.
Die Zeilen 185 bis 195 bedürfen einer etwas ausführlichen Erklärung: Normalerweise würde das Auftreten unzulässiger Werte in der Funktion von X zum Abbruch des Programmes führen, so zum Beispiel wenn der Logarithmus von Werten X<0 gebildet werden oder durch X=0 dividiert werden soll. Die Verarbeitung solcher Funktionen erfordert einen Eingriff ins Betriebssystem: Der Zeiger für die Fehlerbehandlungs-Routine (Speicherplätze $0300 und $0301) wird so (mit Zeile 190) verbogen, daß er jetzt auf einen in den Kassettenpuffer gePOKEten (Zeile 185) Sprungbefehl zeigt.
Infolge dieses Eingriffs gibt nun das Betriebssystem bei Auftreten eines Fehlers nicht mehr Alarm, sondern beginnt mit der Abarbeitung der nächsten (!) Zeile. Restliche Statements in der fehlerträchtigen Zeile werden also nicht mehr beachtet.
Mit diesem Trick wird bewirkt, daß der Sprungbefehl am Ende der Zeile 205 normalerweise ausgeführt wird, bei Auftreten eines Fehlers aber die Zeilen 210 bis 215 abgearbeitet werden. Hier wird je nach Art des Fehlers die Null-Fehler-Flag FE gesetzt oder der unzulässige Wert von X in der Variablen XW festgehalten. Diese Werte sind im weiteren Programmablauf behilflich, unzulässige Werte von X zu vermeiden.
Nach Berechnung aller Werte von X und Ausdruck der entsprechenden Punkte der Funktion (X;Y) in Zeile 220 wird mit den POKE-Befehlen der Zeile 225 der Zeiger für die Fehlerausgabe wieder in den Normalzustand gebracht. Die eingegebene Funktion ist damit fertig geplottet. Das Papier wird vorgeschoben, damit das Ergebnis besichtigt werden kann (Zeile 235). Auf dem Bildschirm erscheint zugleich das Menü (Zeilen 665 bis 720). Abhängig von der Eingabe verzweigt das Programm nun entweder
1) zur Eingabe einer Funktion, die in die gleichen Koordinaten geplotten werden soll, oder
2) zur Eingabe der Parameter für ein neues Koordinatenkreuz oder
3) zur Ausgabe der Kurvendiskussion, die jeweils nur von der letzten dargestellten Funktion erstellt werden kann.
Im Rahmen der Routine für die Berechnung der Kurvendiskussion werden die Fehler-Flags XW und FE dazu verwendet, unzulässige Werte auszulassen.
Nun werden zuerst die Null- beziehungsweise Sprungstellen (Zeilen 285 bis 360) und dann die Extrema (Zeilen 365 bis 390) ermittelt. Doch nun viel Spaß beim Arbeiten mit »Kudiplo«.
(Jürgen Curdt/ev)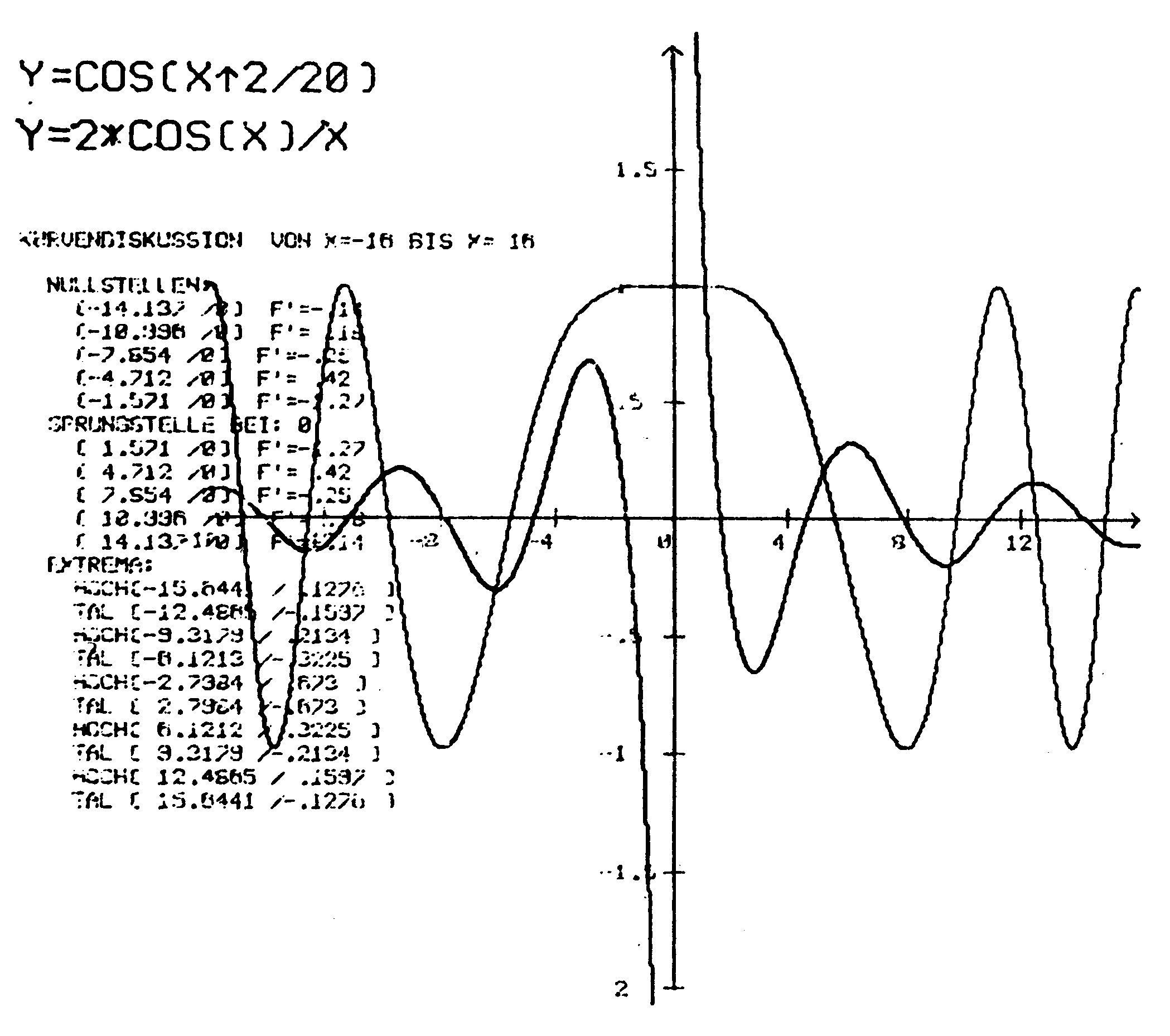
5 rem***********kudiplo*****************
10 rem funktionen diskutieren und
12 rem plotten mit vc-20 +3k
15 rem und printer-plotter vc-1520
20 rem juergen curdt
25 rem kessemeierweg 5
30 rem 493 detmold
35 rem**********************************
40 poke36879,25:goto45
45 xu=-4:xo= 4:yu=-4:yo= 4:oy= 0
50 xn= 280:yn= 0
55 xe=(xo-xu)/16:ye=(yo-yu)/16
60 rem funktion bis 80
65 deffnf(x)=hier wird die funktion eingefuegt
70 f$="hier wird die funktion eingefuegt"
75 deffnf1(x)=(fnf(x+1e-4)-fnf(x-1e-4))/2e-4
80 deffnf2(x)=(fnf1(x+1e-4)-fnf1(x-1e-4))/2e-4
85 open1,6,1:open2,6,2:open3,6,3:open10,6
90 print"{blk}";:ifp=0goto550
95 rem kreuz zeichnen
100 print#3,0:print#2,1
105 ifsvthen170
110 print#10:print#1,"m";0;-440:print#1,"m";0;-200:print#10
115 print#1,"m";80;yn:fori=0to14step2
120 print#1,"i":print#1,"r";0;4:print#1,"j";0;-4
125 print#1,"r";-12;-14
130 print#10,int((xe*i+xu)*100+.5)/100;
135 print#1,"m";80+i*25;yn:print#1,"d";80+(i+2)*25;yn
140 next:print#1,"m";75+i*25;yn-4:print#10,">";
145 print#1,"m";xn;-200
150 fori=0to14step2:print#1,"i":print#1,"r";4;0:print#1,"j";-4;0:print#1,"r";-30;-4
155 j=yu+int(ye*100*i+.5)/100:ifj<>0thenprint#10,j;
160 print#1,"m";xn;i*25-200:print#1,"d";xn;(i+2)*25-200
165 next:print#1,"m";xn-5;i*25-209:print#3,1:print#10,"^";
170 rem kurve plotten
175 print"{clr}{blk}{down}{down}{down}{down} etwas geduld bitte":print#2,sv+3
180 e$="m":fe=0:xw=xu
185 poke832,76:poke833,59:poke834,201
190 poke768,64:poke769,3
195 j=(xo-xu)/400:fori=0to400
200 x=j*i+xu
205 y=hier wird die funktion eingefuegt:goto220
210 e$="m":ifx<0thenxw=x
215 ifx=0thenfe=1:goto230
220 y=y/ye*25+oy:ify>210ory<-210thene$="m":goto230
225 print#1,e$;i+80;y:e$="d"
230 next:poke768,58:poke769,196
235 print#1,"m";0;180-sv*25:print#3,1:print#10,"y="f$;
240 print#1,"m";0;-250
245 goto665
250 print#1,"m";0;160-sv*25
255 print"{clr}die kurvenwerte werden berechnet
260 print#10:print#3,0:ifnotfeandxu=xwthen280
265 iffeandxw=xuthenprint#10,"unzulaessiger wert bei 0":goto275
270 print#10,"unzulaessige werte im bereich":print#10,"von "xu" bis 0 !! - darum nur"
275 xu=xw+.1
280 print#10,"kurvendiskussion von x="xu"bis x="xo:print#10
285 print#10," nullstellen:"
290 a=fnf(xu+.1):s1=xe/40
295 forx=xutoxosteps1
300 ifx=0andfe=1then325
305 f=fnf(x)
310 iff*a<0then335
315 ifabs(f)<1e-6thenc=x:goto465
320 a=f
325 nextx
330 goto370
335 s=x-.1:z=x:c=x-.05
340 iffnf(c)*fnf(z)<0thens=c:goto350
345 z=c
350 c=(s+z)/2
355 ifabs(z-s)<1e-6andabs(fnf(c))<1e-3then465
360 ifabs(z-s)<1e-6thenprint#10," sprungstelle bei:"int(c*1e4+.5)/1e4:goto320
365 goto340
370 print#10," extrema:":a=fnf1(xu+.1):forx=xutoxosteps1
375 ifx=0andfe=1then395
380 f=fnf1(x)
385 iff*a<0then405
390 ifabs(f)<1e-6thenc=x:goto440
395 a=f:nextx
400 print#1,"m";0;-275:close1:close2:close3:close10:end
405 s=x-.1:z=x:c=x-.05
410 iffnf1(c)*fnf1(z)<0thens=c:goto420
415 z=c
420 c=(s+z)/2
425 ifabs(z-s)<1e-6andabs(fnf1(c))<1e-2then440
430 ifabs(z-s)<1e-6then395
435 goto410
440 ifabs(fnf2(c))<1e-5thenprint#10," sattel";:goto455
445 iffnf2(c)>0thenprint#10," tal ";:goto455
450 iffnf2(c)<0thenprint#10," hoch";
455 print#10,"("int(c*1e4+.5)/1e4"/"int(fnf(c)*1e4+.5)/1e4"{left})":goto395
460 rem nullstellen drucken
465 print#10," ("int(c*1e3+.5)/1e3;"/0) f'=";int(fnf1(c)*1e2+.5)/1e2
470 goto320
475 rem parameter waehlen
480 print" die funktion wird dargestellt im bereich"
485 print"{down}von" xu,"bis"xo:print"auf der x-achse"
490 print"{down}von" yu,"bis"yo:print"auf der y-achse"
495 print"{down}{down} sollen die parameter veraendert werden ? j/n"
500 geta$:ifa$="n"thenreturn
505 ifa$<>"j"then500
510 print"{down}{down}unterster wert fuer x":inputxu
515 print"{down}{down}oberster wert fuer x":inputxo
520 xe=(xo-xu)/16:ifxe<=0thenprint"{down}{rvon} unzulaessiger wert {rvof}":goto510
525 ifsgn(xu)=sgn(xo)thenxn=80:goto535
530 xn=abs(xu)*25/xe+80
535 print"{down}{down}unterster wert fuer y":inputyu
540 print"{down}{down}oberster wert fuer y":inputyo
545 ye=(yo-yu)/16:ifye=<0thenprint"{down}{rvon} unzulaessige werte {rvof}":goto535
550 rem eingabe der funktion
555 print"{clr}{blk}funktionen plotten und diskussion drucken {down} mit drucker vc 1520"
560 fori=0to21:print"{CBM-B}";:next:print"{down}"
565 ifnotpthenp=1:gosub475:print"{clr}"
570 print"{down}{down}{down}{down}{down}{down}als funktion wird dar- gestellt:":print"{down}{down}y=";f$
575 print"{down}{down}{down} funktion aendern ? {down} j/n"
580 ifsgn(yu)<>sgn(yo)then595
585 ifyo<=0thenyn=200:oy=abs(yo*25/ye)+200:goto600
590 ifyu>=0thenyn=-200:oy=-200-yu*25/ye:goto600
595 yn=abs(yu)*25/ye-200:oy=yn
600 geta$:ifa$="n"then95
605 ifa$<>"j"then600
610 print"{clr}{down}{down}{down}{down}{down}gib die funktion ein !"
615 print"{down}enthaelt die funktion einen divisor als fun-tion von x, dann den"
620 print" divisor insgesamt in klammern setzen !
625 input"{down}{down}{down}{down}y=";f$
630 print"{clr}{wht}65deffnf(x)="f$"
635 print"205y="f$":goto215"
640 print"70f$="chr$(34)f$chr$(34)"
645 print"45 xu="xu"{left}:xo="xo"{left}:yu="yu"{left}:yo="yo"{left}:oy="oy
650 print"50 xn="xn"{left}:yn="yn:print"sv="sv":p="p":goto45{down}{down}"
655 poke631,19:fori=632to639:pokei,13:next:poke198,8
660 end
665 print"{clr} neue aufgabe ? {down}{down}{down}":print"neue funktion in die gleichen"
670 print"koordinaten drucken g"
675 print"{down}{down}neue koordinaten drucken n"
680 print"{down}{down}kurvendiskussion ausgeben k"
685 print"ende e
690 geta$:ifa$="n"thenrun
695 ifa$="k"then250
700 ifa$="e"then400
705 ifa$<>"g"then690
710 sv=sv+1
715 print"{clr}";:gosub570
720 goto170
