Strukturiertes Programmieren
Strukturiertes Programmieren ist keineswegs so schwierig wie es sich anhört. Neben etwas Theorie wollen wir ein kleines aber ausbaufähiges Spiel entwerfen.


Im letzten Heft gab ich Ihnen einige Regeln, die das Strukturieren des Programmcodes betreffen. Eigentlich war dieser Bericht zu früh dran. Denn bevor man sich an seinen Computer setzt und das Programm eintippt, ist eine Menge Vorarbeit zu leisten. Die wichtigste Arbeit besteht dabei im Nachdenken. Nachdenken vor allem darüber, was das Programm, das man schreiben will, eigentlich tun soll, wie man es am effektivsten aufbaut. Und dabei werden die meisten und verhängnisvollsten Fehler gemacht. Diese Fehler ziehen sich durch das gesamte »Software-Projekt« hindurch und entscheiden später über den Erfolg oder Mißerfolg des Programms. Und je später ein Fehler endeckt wird, desto größer wird der Aufwand, den man betreiben muß, um diesen Fehler zu beheben. Das bedeutet ganz einfach, daß man am Anfang sehr aufmerksam sein muß, und jeden Schritt, jede Idee lieber einmal mehr als einmal zu wenig überdenken sollte.
Gerade dann, wenn das Programm wahrscheinlich etwas größer wird, tut man gut daran, es in kleinere Einheiten aufzuteilen. Diese Einheiten werden auch Module genannt. Gebräuchlich sind auch die Begriffe »Unterprogramm«, »Subroutine« oder auch »Prozeduren« (zum Beispiel in Pascal). Gemeint ist in der Regel immer das gleiche.
Bei großen und komplexen Programmpaketen besteht eine der wichtigsten Aufgaben in der Modularisierung eines Programms. Das heißt aber auch, daß, wenn diese Aufgabe erste einmal gelöst ist, der Rest um so einfacher und schneller von der Hand geht.
Wie ein Spiel entsteht
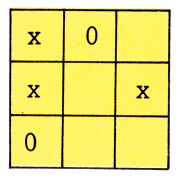
Wenden wir uns jetzt einem neuen Beispiel zu. Ich möchte mit Ihnen ein kleines und einfaches Spiel entwerfen. Die Spielregeln sind sehr einfach. Wir wollen den Computer veranlassen, gegen uns zu spielen. In ein Spielfeld von 3 x 3 Feldern setzen die Spieler (der Computer und wir) abwechselnd eine Null oder ein X. Wir setzen die X. Wer als erster drei Zeichen in einer Reihe hat, hat gewonnen. Eine Reihe heißt hier senkrecht, waagerecht oder diagonal. Das Spielfeld und eine typische Spielsituation sind in Bild 1a und 1b zu sehen.
Wir wollen unser Spielfeld jetzt numerieren, jedes Feld erhält eine Nummer (Bild 1c). Jetzt schreiben wir uns auf, was in jedem Feld steht:
1 x 2 0 3 - 4 x 5 - 6 x 7 0 8 - 9 -
Ein Strich bedeutet hier ein leeres Feld.
Ersetze x durch 1
0 durch —1
— durch 0
Der Grund dafür, daß wir gerade diese Zahlen nehmen, ist jetzt noch nicht so klar, im Moment ist es einfach ein Gefühl für Symmetrie. Wir werden aber sehen, daß diese Wahl zweckmäßig ist.
Damit können wir den Spielstand so beschreiben:
| Feld | Inhalt |
|---|---|
| 1 | 1 |
| 2 | -1 |
| 3 | 0 |
| 4 | 1 |
| 5 | 0 |
| 6 | 1 |
| 7 | -1 |
| 8 | 0 |
| 9 | 0 |
Diesen (und auch jeden anderen) Spielstand legen wir in einem Array SS ab (SS steht für Spielstand). So oft sich also der Spielstand ändert, ändert sich auch der Inhalt des Arrays SS. SS(5) enthält also immer den Inhalt des mittleren Feldes, eine 1, wenn wir einen Stein (x) auf das Feld gesetzt haben, eine —1, wenn der Computer seinen Spielstein darauf gesetzt hat, oder eine 0, wenn das Feld noch nicht besetzt ist.
Jetzt können wir (und vor allem der Computer) herausfinden, welches Feld besetzt ist, und auch, durch wen es besetzt wurde, aber wir müssen den Compuer ja noch dazu bringen, einen vernünftigen Spielzug zu machen. Das bedeutet, er muß sperren, wenn wir schon zwei Felder einer Reihe besetzt haben, und er soll auch erkennen, wenn er schon zwei Felder einer Reihe besetzt hat, wo er seinen Siegzug hinzusetzen hat. Wir brauchen also eine Methode, um den Spielstand zu bewerten.
Dazu schaffen wir ein zweites Array, das wir BW nennen (BW steht für Bewertung). BW enthält die Summen jeder Reihe, der waagerechten, der senkrechten und der diagonalen. Insgesamt haben wir acht Reihen, so daß auch BW nicht größer zu sein braucht. Und so wird jedes Element von BW berechnet:
| 1 | 0 | = SS(1) + SS(2) + SS(3) | oberste Reihe |
| 2 | 2 | = SS(4) + SS(5) + SS(6) | zweite Reihe |
| 3 | -1 | = SS(7) + SS(8) + SS(9) | dritte Reihe |
| 4 | 1 | = SS(1) + SS(4) + SS(7) | linke Spalte |
| 5 | -1 | = SS(2) + SS(5) + SS(8) | mittlere Spalte |
| 6 | 1 | = SS(3) + SS(6) + SS(9) | rechte Spalte |
| 7 | 1 | = SS(1) + SS(5) + SS(9) | vordere Diagonale |
| 8 | -1 | = SS(3) + SS(5) + SS(7) | hintere Diagonale |
Diese Werte geben selbstverständlich nur den oben im Beispiel vorgegebenen Spielstand wieder. Aber wir können jetzt erkennen, daß das Array BW uns Informationen über die aktuelle Spielsituation liefert: Immer, wenn ein Element von BW den Wert 2 hat, erkennt der Computer, daß für ihn Gefahr im Verzuge ist. Die 2 bedeutet nämlich, daß in einer Reihe schon zweimal ein Sein gesetzt wurde. Damit dürfte die nächste Aufgabe des Computers schon klar sein: Er muß seinen nächsten Stein in das dritte Feld der fast kompletten Reihe setzen! Doch wie soll er das freie Feld finden? Wir machen es uns einfach: Er soll so lange einen Stein in ein freies Feld setzen, bis eine erneute Überprüfung des Arrays BW ergibt, daß kein Element mehr den Wert 2 hat. Und wirklich, wenn der Computer zufällig das richtige Feld erwischt hat, wird ja dieses Feld mit einer —1 belegt. Dadurch wird in dem BW-Feld, in dem eine 2 steht, —1 hinzuaddiert, also 1 abgezogen. Damit existiert in diesem Moment keine gefährliche Situation mehr, jedenfalls nicht für den Computer. Ich sagte gerade, daß der Computer ganz zufällig irgendein freies Feld belegt, um dann nachzuprüfen, ob sich dadurch eine Entschärfung der für ihn gefährlichen Situation ergibt. Falls er ein Feld belegt hat, das nicht zu einer Lösung führt (das heißt die 2 im Feld BW wird nicht verändert), müssen wir natürlich dafür sogen, daß diser Zug wieder zurückgenommen wird. In diesem Fall braucht also dieses Feld nur wieder mit einer 0 belegt zu werden. Aber warum meinte ich »zufällig«? Nun, wir könnten das Spielfeld systematisch druchsuchen lassen, aber dann wäre jeder Zug vorhersehbar und bei einem Spiel wäre das nicht besonders interessant.
Die Funktionen
Wir legen jetzt also fest, daß der Computer nur dann zu sperren braucht, wenn sich eine für ihn gefährliche Situation ergibt, wenn also zwei Felder in einer Reihe durch ein X besetzt sind. Alle anderen Fälle interessieren ihn nicht besonders, in diesen Fällen setzt er seine Steine ganz zufällig auf ein freies Feld. Selbstverständlich bemerkt er auch, wenn er selbst zwei Felder besetzt hat. Dann versucht er natürlich, daß dritte Feld auch zu belegen. Und last not least, erkennen soll der Computer auch, wenn er oder wir gewonnen haben. Und das erkennt er dann, wenn die Summe einer Reihe +/-3 ergibt.
So, mit diesen Ideen können wir schon etwas anfangen. Wir versuchen jetzt, die einzelnen Funktionen des Programms festzulegen. In welche Teilaufgaben können wir das Problem zerlegen? Als erstes brauchen wir eine Initialisierung der Variablen. Das Spielfeld soll auch angezeigt werden, das ist ein weiterer Teil. Dann gibt es einmal den Computerzug und auch unseren Spielzug. Und auch die Überprüfung auf Spielende darf nicht fehlen.
Daraus ergibt sich:
| Funktion | Beginn einer Zeile |
|---|---|
| Hauptprogramm | 10 |
| Initialisierung des Spielfeldes | 1000 |
| Anzeigen des Spielfeldes | 2000 |
| Zug holen | 3000 |
| Auf Spielende prüfen | 4000 |
| Computerzug | 5000 |
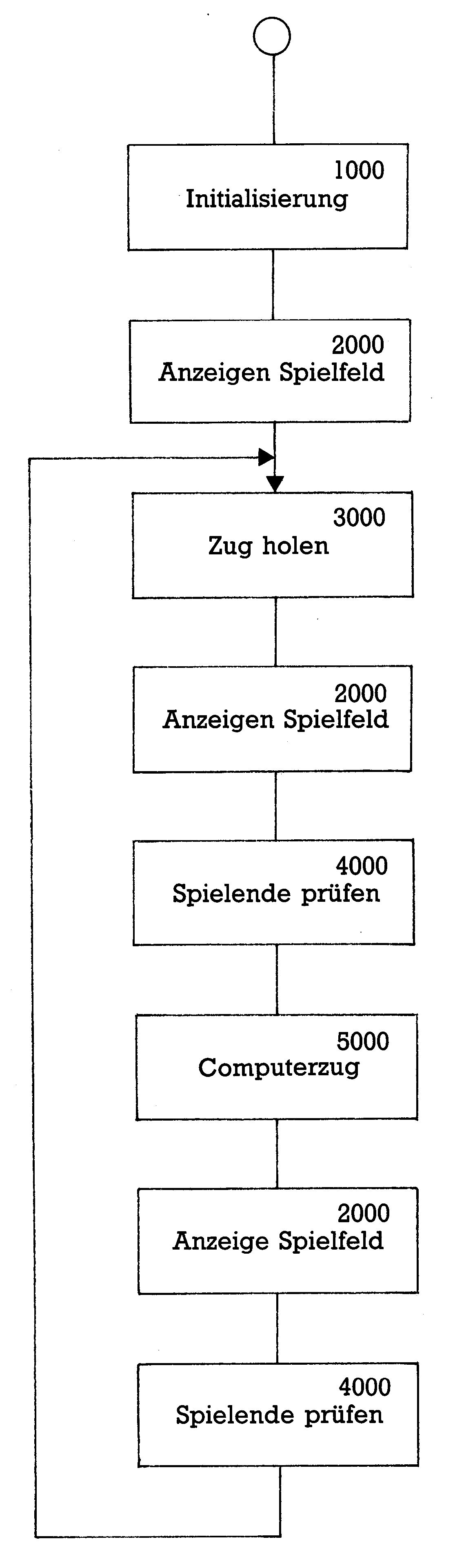
In der Reihenfolge wie sie Bild 2 zeigt, werden die einzelnen Module aufgerufen. Deshalb nennt man dies auch ein Ablaufdiagramm. Manche dieser Module müssen noch weiter unterteilt werden. Zum Beispiel der Modul SPIELENDE (4000): Um ein Spielende zu erreichen, gibt es mindestens zwei Möglichkeiten: Entweder ist eine Reihe mit drei gleichen Steinen besetzt oder aber das Spielfeld ist voll. Dann gibt es ein Unentschieden.
Um das herauszufinden, erstellen wir eine Routine zum BEWERTEN (6000) des Spielfeldes. In diesem Modul wird das Array BW erzeugt (siehe oben).
Wie steht es nun mit dem Modul COMPUTERZUG (5000)?
Ganz klar, auch der Computer muß wissen, wie das Spielfeld jetzt aussieht. Deswegen rufen wir auch hier den Modul BEWERTEN auf. Aus dieser Bewertung heraus können sich drei Möglichkeiten ergeben:
- Der Computer hat schon eine Reihe mit zwei Steinen besetzt und das dritte Feld ist noch frei (das heißt ein Element von BW hat den Wert —2). Dann führt er einen SIEGZUG (7000) aus. Da wir schon vorhin davon sprachen, daß der Computer seinen Stein zufällig setzt, müssen wir hier den Modul ZURÜCKNEHMEN (10000) berücksichtigen
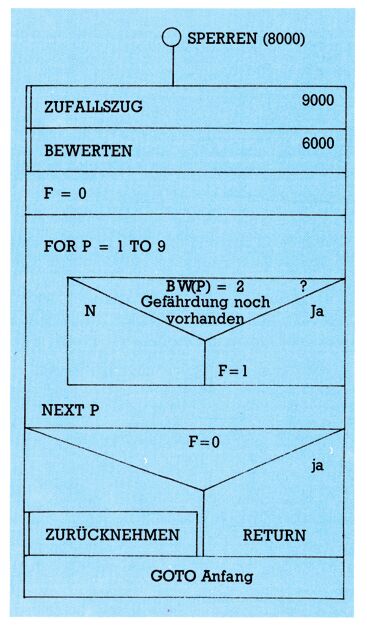
- Die Gegner — also wir — haben schon zwei Steine in einer Reihe. Wenn das dritte Feld dieser Reihe noch frei ist, ärgert uns der Computer, indem er dieses Feld versucht zu SPERREN (8000).
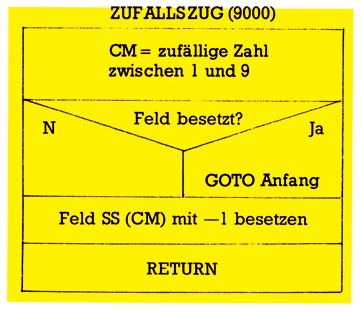
- Im dritten Fall ergibt sich weder das eine noch das andere, und der Computer macht einen ZUFALLSZUG (9000).
Selbst wenn wir die Frechheit besitzen, den Computer auszutricksen, in dem wir zwei Reihen mit je zwei Steinen und einem freien Feld erspielen können, merkt er das und verabschiedet sich nachtragend.
Damit wäre auch diese Ebene definiert.
Unser Programm sieht jetzt so aus:
| 0 | HAUPTPROGRAMM | 10 |
| 1.1. | INITIALISIERUNG | 1000 |
| 1.2. | ANZEIGE | 2000 |
| 1.3. | ZUG HOLEN | 3000 |
| 1.4. | SPIELENDE | 4000 |
| 1.5. | COMPUTERZUG | 5000 |
| 2.1. | BEWERTEN | 6000 |
| 2.2. | SIEGZUG | 7000 |
| 2.3. | SPERREN | 8000 |
| 2.4. | ZUFALLSZUG | 9000 |
| 3.1. | ZURÜCKNEHMEN | 10000 |
Jetzt haben wir alle notwendigen Module benannt. Daraus erstellen wir ein Übersichtsprogramm. In diesem Übersichtsprogramm werden alle Module grafisch dargestellt und zwar in ihren Abhängigkeiten voneinander (siehe Bild 3).
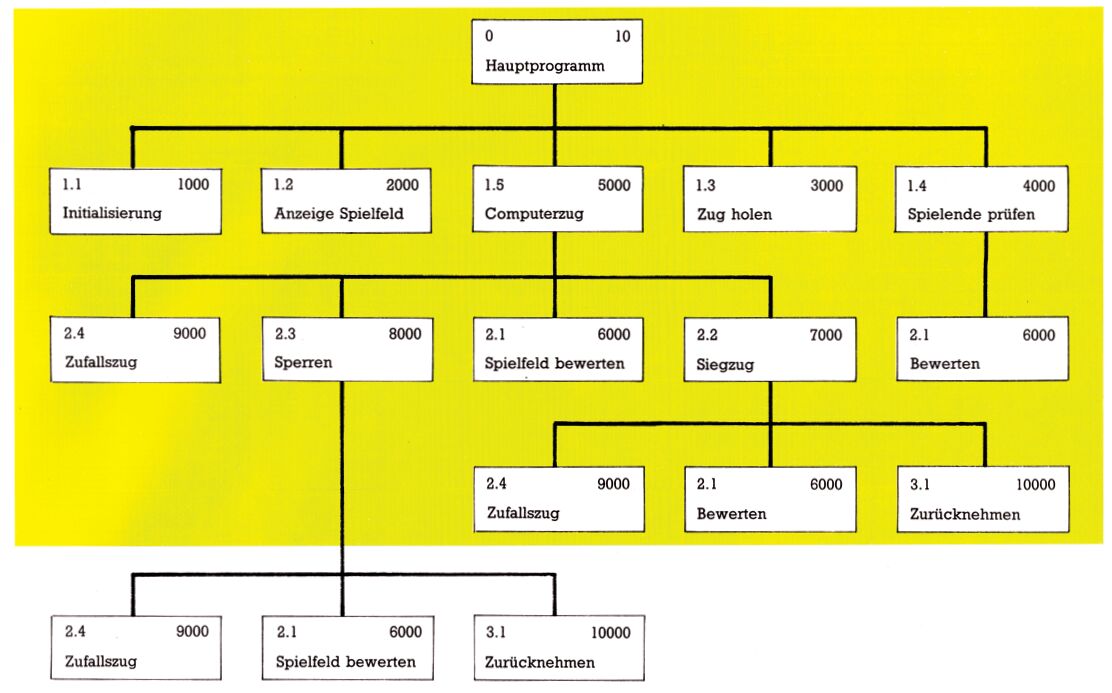
Die Beziehung zwischen den einzelnen Unterprogrammen ist: »ruft auf«. Das Hauptprogramm also ruft auf: INITIALISIERUNG, ANZEIGEN, ZUG HOLEN, SPIELENDE PRÜFEN und COMPUTERZUG. Manche der anderen Module werden nur nach einer bedingten Verzweigung (IF ... THEN GOSUB ...) durchlaufen. Das spielt bei dieser Übersicht jedoch keine Rolle.
So, jetzt sind wir so weit, daß wir uns die einzelnen Teile etwas genauer anschauen können. Fangen wir wieder mit dem Hauptprogramm an. Oben im Ablaufdiagramm ist es eigentlich schon vollständig beschrieben. Hier könnten wir schon sofort das Coding hinschreiben (Listing 1).
10 REM *******************************
20 REM * KREUZ UND QUER *
30 REM *******************************
90 PRINT"{CLR}"
100 DIMSS(9):DIMBW(8)
110 GOSUB1000:REM SPIELFELD INITIALISIEREN
120 GOSUB2000:REM ANZEIGEN
130 GOSUB3000:REM ZUG HOLEN
140 GOSUB2000:REM ANZEIGEN
150 GOSUB4000:REM AUF SPIELENDE PRUEFEN
160 GOSUB5000:REM COMPUTERZUG
170 GOSUB2000:REM ANZEIGEN
180 GOSUB4000:REM AUF SPIELENDE PRUEFEN
190 GOTO130
Wenn Sie dieses Listing mit dem Ablaufdiagramm (Bild 2) vergleichen, sehen Sie die direkte Umsetzung unserer Überlegungen. Lediglich der Programmkopf, das Löschen des Bildschirms (Zeile 90) und die Dimensionierung unserer Arrays (Zeile 100) kommt noch hinzu. Diese Zeile ist in unserem Beispiel zwar nicht notwendig (der C 64 läßt Arrays bis 11 Elemente zu ohne sie dimensionieren zu müssen), aber da wir ja weiterdenken, bereiten wir unser Programm schon für spätere Erweiterungen vor (es könnte ja sein, daß unser Spielfeld vergrößert werden soll). Außerdem erkennen wir schon im Hauptspeicher, welche Variablen für das ganze Programm benötigt werden. Man spricht hier auch von »globalen Variablen«, im Gegensatz zu »lokalen Variablen«, die nur innerhalb eines Moduls wichtig sind.
Jetzt, nachdem unser Hauptprogramm »steht«, knöpfen wir uns das nächste Modul vor.
INITIALISIERUNG
In diesem Modul wollen wir die Felder unseres Spielfeldes löschen. Das bedeutet, wir löschen Array SS (Listing 2).
1000 REM---------------- 1010 REM INITIALISIERUNG 1020 : 1100 FORP=1TO3 1110 :SS(P)=0 1120 NEXTP 1130 RETURN
Ich will für einige der folgenden Module das Struktprogramm erstellen. Die Umsetzung in ein ablauffähiges Programm überlasse ich Ihnen. Eine Ausnahme werde ich machen mit den Modulen COMPUTERZUG, SPIELFELD BEWERTEN und ZURÜCKNEHMEN.
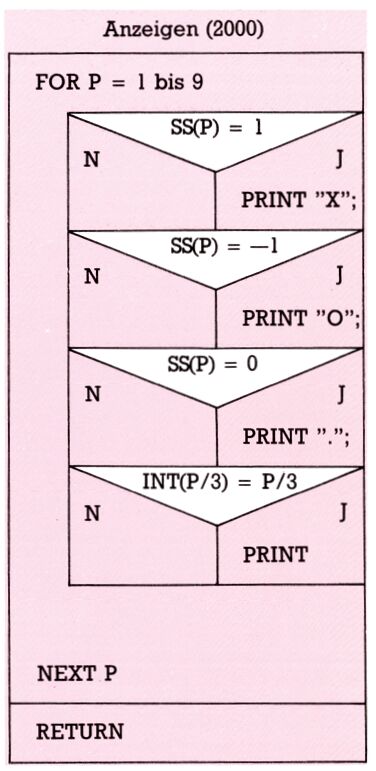
Modul SPIELFELD ANZEIGEN (2000/) (Bild 4)
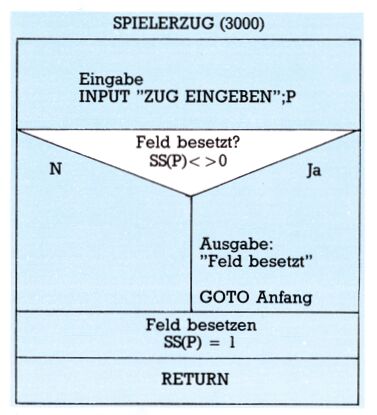
Modul SPIELERZUG (3000/) (Bild 5)
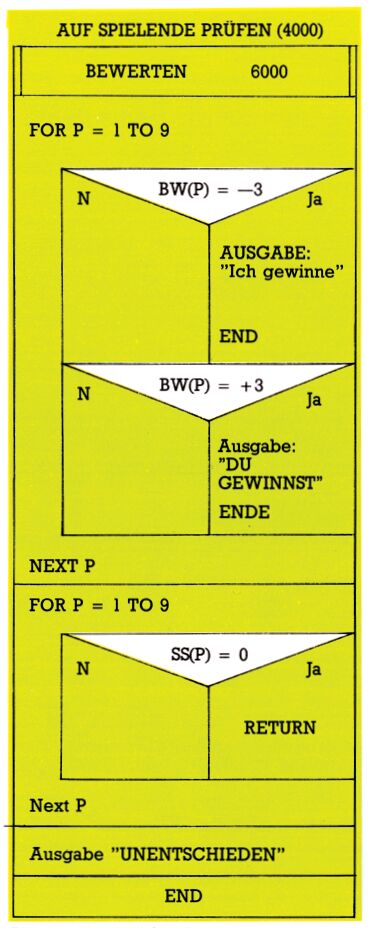
Modul SPIELENDE PRÜFEN (4000/) (Bild 6)
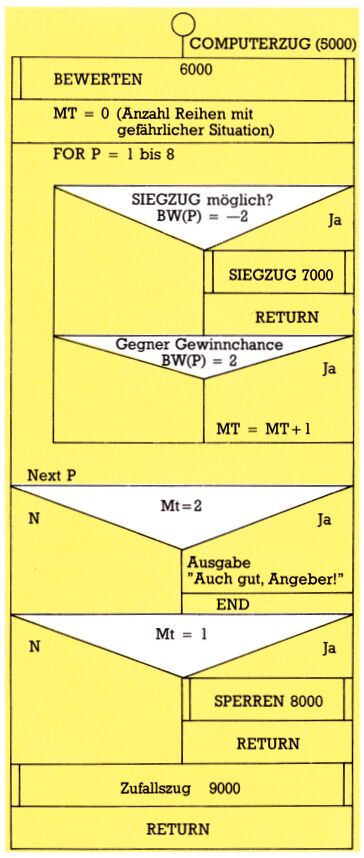
Modul COMPUTERZUG (5000/) (Bild 7)
Und dann der versprochene Code
dazu: (Listing 3)
5000 REM------------------------------ 5010 REM COMPUTERZUG 5020 5030 GOSUB6000 5040 MT=0 5050 FORP=1TO8 5060 :IFBW(P)=-2THENGOSUB7000:RETURN 5070 :IFBW(P)=2THENMT=MT+1 5080 NEXTP 5090 IFMT=2THENPRINT "AUCH GUT. ANGEBER!":END 5100 IFMT=1THENGOSUB8000:RETURN 5110 GOSUB9000 5120 RETURN 5130 :
Modul SPIELFELD BEWERTEN (6000)
Hier wird das Array BW definiert. Man könnte dieses Modul natürlich mit einer Schleife lösen, aber eigentlich lohnt sich der Aufwand nicht (Listing 4).
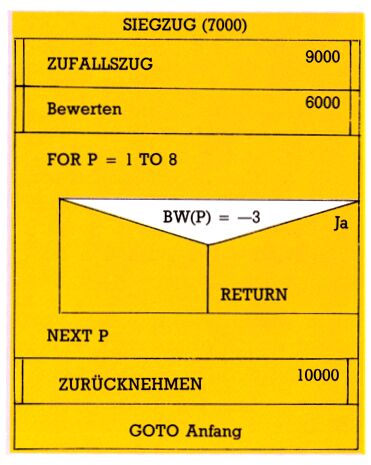
Der Modul SIEGZUG (7000) ist auch schnell gelöst (Bild 8).
Modul SPERREN (8000/) (Bild 9)
Modul ZUFALLSZUG (9000/) (Bild 10)
Modul ZURÜCKNEHMEN (100000)
Und dies ist die einfachste Routine, ein Zweizeiler:
10000 REM ------------------------------------- 10010 REM ZURÜCKNEHMEN 10030 : 10040 SS(CM) = 0 10050 RETURN
6000 REM-------------------- 6010 REM SPIELFELD BEWERTEN 6020 : 6030 : 6040 BW(1)=SS(1)+SS(2)+SS(3) 6050 BW(2)=SS(4)+SS(5)+SS(6) 6060 BW(3)=SS(7)+SS(8)+SS(9) 6070 BW(4)=SS(1)+SS(4)+SS(7) 6080 BW(5)=SS(2)+SS(5)+SS(8) 6090 BW(6)=SS(3)+SS(6)+SS(9) 6100 BW(7)=SS(1)+SS(5)+SS(9) 6110 BW(8)=SS(3)+SS(5)+SS(7) 6120 RETURN 6130 :
So, daß war das ganze Programm! Eigentlich sollte es Ihnen gelingen, anhand der Struktogramme das Programm zu schreiben. Aber Sie sehen schon jetzt, daß eine Änderung des Programms ganz einfach ist. Man kann sich jeden Modul einzeln vornehmen und ihn je nach Wunsch ändern oder erweitern. Dazu bietet sich zum Beispiel der Modul SPIELFELD ANZEIGEN (2000) an (Bild 4). Man kann die Bildschirmdarstellung sehr gut verbessern, ohne die Programmstruktur zu ändern. Man könnte auch die Strategie des Computers im Modul COMPUTERZUG (5000) verbessern (Bild 7), zum Beispiel soll er zuerst das Feld 5 besetzen (wenn es noch frei ist). Das bringt Spielvorteile (vorausgesetzt, es besteht keine Bedrohung oder eine Gewinnposition ...). Auch könnte man abwechselnd den Computer oder den Mitspieler anfangen lassen zu spielen. Ändern Sie das Programm so ab, daß auch mehrere Spiele durchgeführt werden können und das darüber Buch geführt wird. Sie werden feststellen, daß Änderungen durch die Modularisierung relativ einfach gemacht werden können. Erkennen Sie den Vorteil dieser Programmstrukturierung?
Was wir hier gemacht haben, ist ein Top-down-Entwurf. Wir haben bei dem Modul an der Spitze der Hierarchie angefangen (beim Steuermodul oder Hauptprogramm) und entwickelten dann die weiteren Module. Es gibt noch eine andere Methode. Sie nennt man Bottom-up-Methode. Bei dieser Methode ist es genau umgekehrt: Hier fängt man an der untersten Hierarchiestufe an und endet an der obersten.
Im nächsten Heft stelle ich Ihnen die Elemente der Flußdiagramme und auch die Struktogramme ausführlich vor. Und wenn Sie Lust haben, schicken Sie uns doch Ihre Lösungsvorschläge des Programms. Ich könnte mir vorstellen, daß wir einige interessante Lösungen erhalten werden.
(Dieses Beispiel ist zum Teil entnommen aus dem Buch Commodore 64, Programmieren leicht gemacht, aus dem Birkhäuser Verlag (siehe auch unsere Buchbesprechung)).
TOP-DOWN-Vorgehensweise
Top-Down ist eine bestimmte Vorgehensweise bei der Entwicklung und beim Test von Programmen. Sie basiert auf hierarchischen Strukturen und dient als sinnvolle Ergänzung zur strukturierten Programmierung. Zuerst werden die im Sinne der Hierarchie obersten Programmteile entworfen, codiert und getestet, ehe zu Programmteilen der nächst niedrigeren Hierarchiestufe übergegangen wird. Dadurch sind Programmierobjekte besser überschaubar, allgemeine Anforderungen können zuerst, Details später hinzugefügt werden. Weil man sich bei diesem Vorgehen am Anfang mehr Mühe machen muß, wird durch die Betrachtung des Gesamtsystems das frühzeitige Erkennen von Entwurfsfehlern erleichtert. Der Einbau von Entwurfsänderungen ist in den meisten Fällen problemlos.
BOTTOM-UP
Im Gegensatz zum TOP-DOWN-Entwurf fängt man in einer hierarchischen Programmstruktur auf der untersten Stufe an, entwickelt die einzelnen Komponenten, testet sie einzeln. Ist der Test erfolgreich verlaufen, geht man zur nächsten, höheren Hierarchiestufe weiter und setzt die Arbeit ähnlich fort. So wird ein Programm stufenweise von unten nach oben entwickelt und getestet. Diese Vorgehensweise hat zweifellos Vorteile, man darf jedoch ihre Nachteile nicht übersehen:
Je höher die Integrationsstufe, also je höher man in der Hierarchie gestiegen ist, um so schwieriger ist die Ursache von Fehlern zu entdecken.
Änderungen »in der letzten Minute« verursachen wiederum neue Fehler und verschlechtern die Qualität gut konzipierter Programme.
Zusammenhängende Ergebnisse werden während der ganzen Entwicklungsphase nicht sichtbar.
